

Ukupni troškovi vožnje vlaka na nekoj redovitoj liniji iznose kuna, pri čemu je prosječna brzina vožnje vlaka u Pri kojoj će brzini troškovi vožnje vlaka biti najmanji? Pri kojim će se brzinama troškovi vožnje vlaka povećavati, a pri kojim smanjivati?

Da bismo mogli odgovoriti na ova pitanja, trebali bismo znati kako izgleda funkcija koja opisuje troškove. O tome će biti riječi u ovoj jedinici.
Podsjetimo se, domena ili
Uočimo da nazivnik u razlomku ne smije biti jednak nuli.
Sljedeći je korak određivanje nultočaka funkcije. Prisjetimo se.
Nultočka realne funkcije je točka presjeka grafa funkcije i osi
Primjer 1.
Odredimo nultočke funkcije zadane pravilom
Trebamo odrediti vrijednosti broja
za koji je
znači
Znamo da će razlomak biti jednak nula ako je njegov brojnik jednak nula. Zbog toga trebamo riješiti jednadžbu To je jednostavna kvadratna jednadžba koju znamo riješiti na razne načine te su rješenja i Dobivene su vrijednosti nulišta zadane funkcije Konačno, nultočke funkcije su točke s koordinatama i
Povežite zadane funkcije s njihovim nultočkama.
|
|
i |
|
|
nema nultočaka |
|
|
|
|
|
|
|
|
i |
|
|
i |
Nakon određivanja domene i nultočaka funkcije, ako postoje, slijedi određivanje tijeka funkcije. To znači da trebamo odrediti gdje funkcija raste, a gdje pada. U prethodnim smo jedinicama naučili da nam za to treba derivacija funkcije. Prisjetimo se.
Kako bismo odredili intervale gdje je odnosno prvo trebamo odrediti stacionarne točke, tj. točke takve da je
Ako derivacija funkcije u stacionarnoj točki
Primjer 2.
Odredimo intervale monotonosti funkcije Ima li ta funkcija ekstrem?
Prvo ćemo odrediti derivaciju funkcije
Stacionarne točke tražimo kao rješenja jednadžbe
je stacionarna točka.
Pogledajmo kakav je predznak derivacije ispred, a kakav iza stacionarne točke.
Uvrstimo neki broj manji od
primjerice
Slijedi
Broj je veći od a
Kada te podatke složimo u tablicu i primijenimo naučeno, slijedi:
Pogledajmo što se događa u stacionarnoj točki. Derivacija mijenja predznak, funkcija je bila rastuća ispred, a padajuća iza pa zaključujemo da funkcija ima maksimalnu vrijednost.
Uvrstimo u pravilo funkcije
Lokalni maksimum je
Pogledajmo još jednom zadanu funkciju
Jesmo li mogli njezin ekstrem, a iz toga i pad i rast, odrediti na neki drugi način?
S obzirom na to da je
kvadratna funkcija, znamo da postiže minimalnu ili maksimalnu vrijednost u tjemenu funkcije. Apscisu tjemena računali smo s pomoću formule
a to je upravo stacionarna točka dobivena s pomoću derivacije. S obzirom na to da je vodeći koeficijent negativan, znamo oblik grafa funkcije. Funkcija prvo raste, postiže maksimum pa dalje pada.
Sve ćemo navedene korake provesti pri crtanju grafa funkcije.
Primjer 3.
Nacrtajmo graf funkcije
Pogledajmo rješenje u sljedećem videozapisu.
Riješite sada uvodni zadatak.
Ukupni troškovi vožnje vlaka na nekoj redovitoj liniji iznose
kuna, pri čemu je
prosječna brzina vožnje vlaka u
Pri kojoj će brzini troškovi vožnje vlaka biti najmanji? Pri kojim će se brzinama troškovi vožnje vlaka povećavati, a pri kojim smanjivati?
1. Domena funkcije
Iz zapisa vidimo da nazivnik ne smije biti jednak nula, a iz stvarne situacije znamo da brzina mora biti pozitivna. Stoga će domena ove funkcije biti pozitivni realni brojevi.
2. Nultočke funkcije
pa ova jednadžba nema realnih rješenja.
3. Intervali monotonosti i ekstremi
Odredimo derivaciju funkcije
i tražimo stacionarne točke,
Broj između
i
primjerice
uvrstimo u derivaciju,
Za broj veći od
primjerice 10, vrijedi:
Očito je u
lokalni minimum i
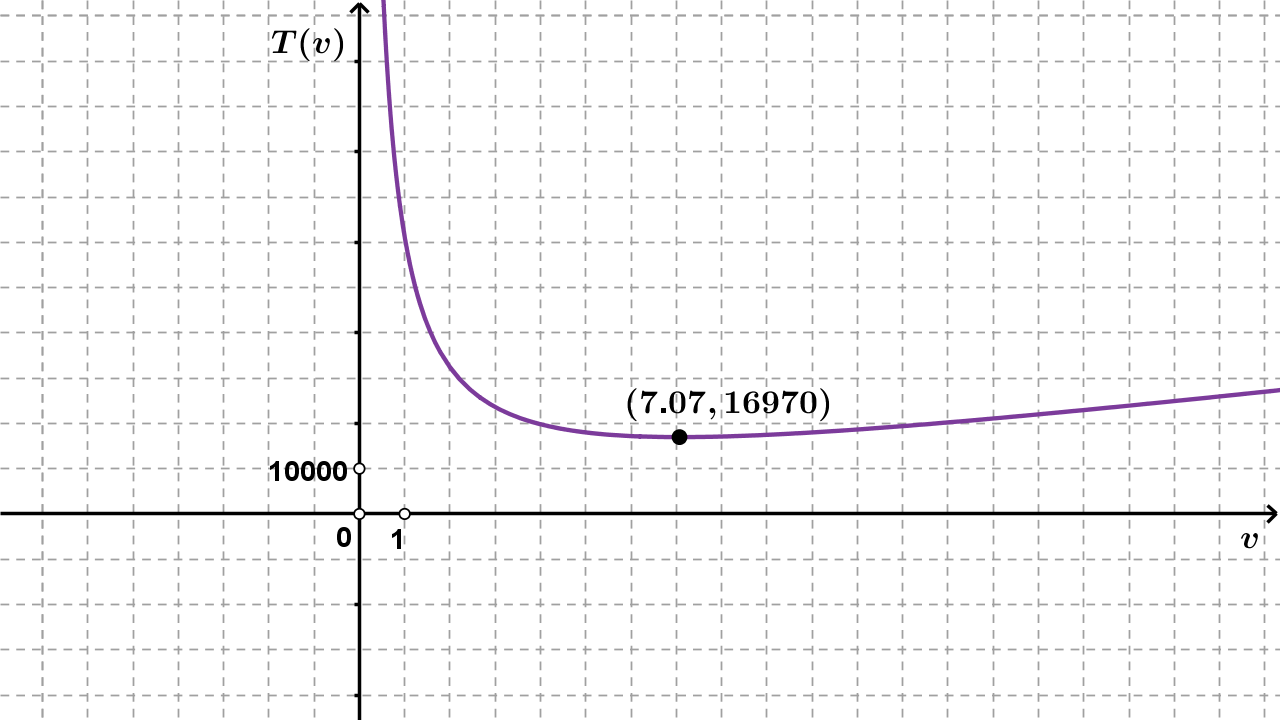
Nacrtajmo tablicu tijeka funkcije.
Nacrtajmo sada graf funkcije.
Troškovi su vlaka minimalni pri brzini od
i iznose
kuna. Iz grafa vidimo da se troškovi smanjuju od brzine
do
a pri brzinama većim od
troškovi rastu.
U prethodnim smo zadatcima računali derivaciju funkcije, crtali tablice tijeka funkcije te nacrtali graf funkcije. Pokušajte obrnuto.
Za funkciju
vrijedi da je
Skicirajte graf funkcije
ako je na slici prikazan graf derivacije funkcije
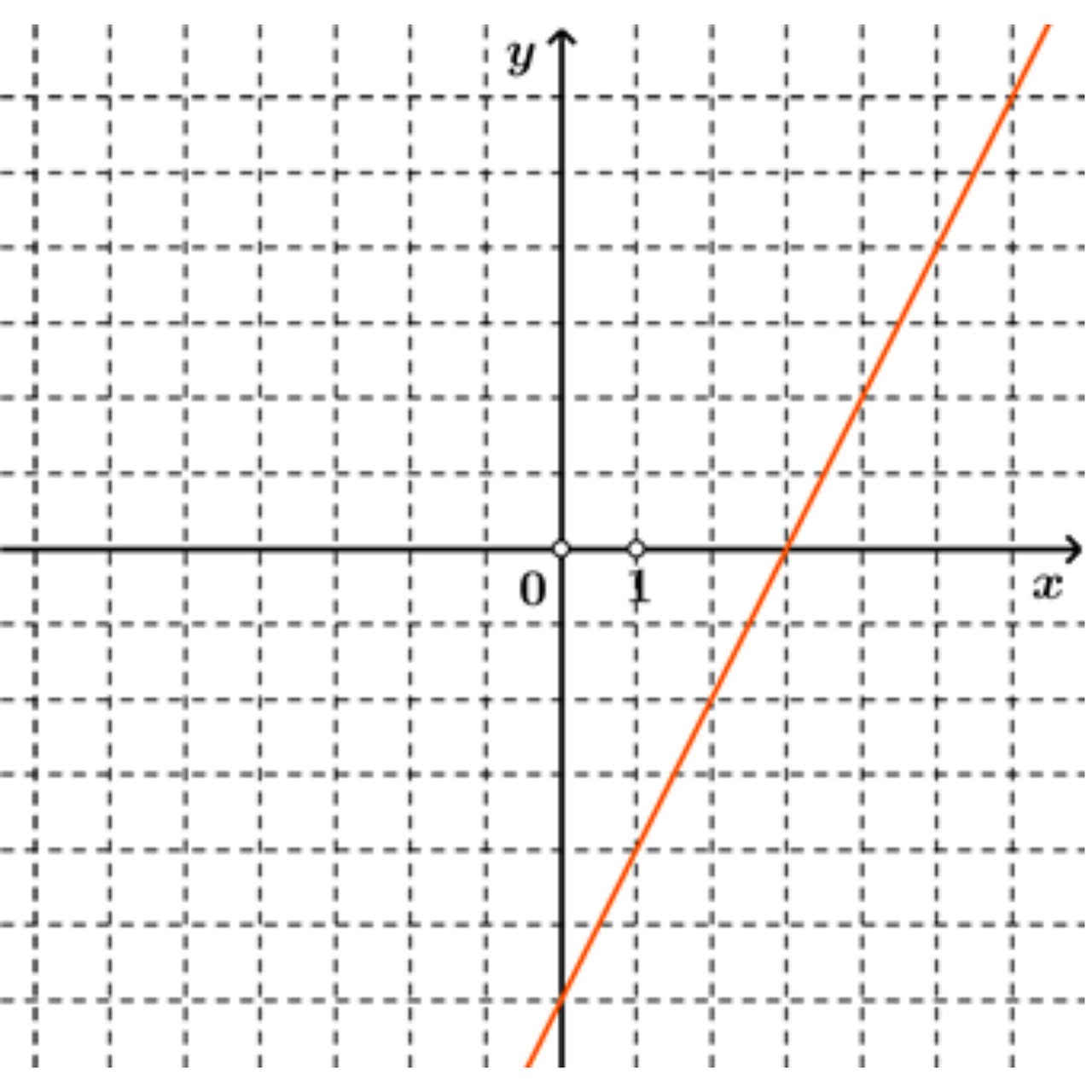
Iz grafa derivacije funkcije vidimo da funkcija pada na intervalu
i raste na intervalu
Znači da u točki s apscisom
ima minimum. Znamo gdje su joj nultočke, ali ne znamo točno vrijednost minimuma pa je ovo jedno od mogućih rješenja.
Poredajte korake koje trebamo provesti kako bismo nacrtali graf funkcije.