Matematika 4 - 6.2 Operacije s događajima

Na početku...

Sigurno ste nekad igrali igru Čovječe, ne ljuti se. Bacali ste jednu kocku i očekivali da padne neki broj.

Je li mogao pasti broj $7 ?$
Jesu li mogli pasti brojevi manji od $7 ?$

Bacanje kocke u igri Čovječe, ne ljuti se

Prisjetimo se, prostor elementarnih događaja za bacanje jedne kocke je

Ω = \{

\} .

null

Broj $7$ nije mogao pasti pa ćemo ga na zvati

događaj i označiti kao prazan skup

\emptyset .

Pri bacanju kocke ćemo sigurno dobiti broj koji je manji od

7,

taj je događaj jednak prostoru elementarnih događaja

Ω

pa se naziva

događaj.

null

Suprotni događaj

Bacamo jednu kocku. Neka je događaj $A = \{pao je paran broj\}$ i $B = \{pao je neparan broj\} .$

Znamo da se pri bacanju kocke neće ostvariti događaj $A$ ako se ostvario događaj $B$ i da se neće ostvariti događaj $B$ ako se ostvario događaj $A .$ Štoviše, ako se neće ostvariti događaj $A,$ onda će se sigurno ostvariti događaj $B,$ i obrnuto.

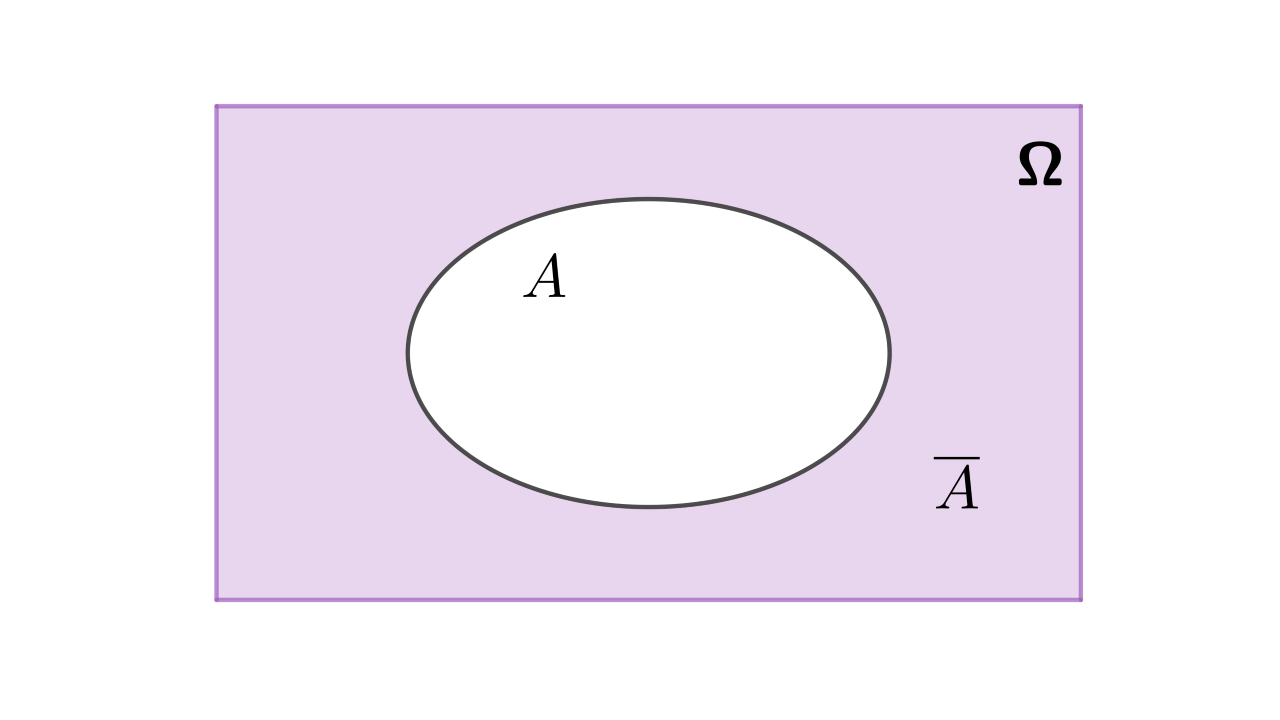
Ako se u nekom slučajnom pokusu ne ostvari događaj $A,$ ostvarit će se njegov suprotni događaj ili komplement koji označavamo s $\bar{A} .$

Događaji su skupovi pa ćemo ih prikazivati Vennovim dijagramima.

Zanimljivost

Engleski logičar i filozof John Venn (1834. – 1923.) prvi je opisao dijagram 1880-ih. Nazvao ih je eulerijskim krugovima po švicarskom matematičaru Leonardu Euleru, koji je 1700-ih osmislio slične dijagrame.

Vennov dijagram prikazuje suprotni događaj ili komplement — Suprotni događaji

Riješite sljedeće zadatke.

Presjek događaja

Primjer 1.

Bacamo kocku jedanput. Promotrimo sljedeća tri događaja: $A = \{pao je broj veći od 3\},$ $B = \{pao je prost broj\}$ i $C = \{pao je broj 5\} .$ U kakvu su odnosu ta tri događaja?

Prikažimo događaje Vennovim dijagramom. Pogledajmo animaciju.

Presjek dvaju događaja, $A \cap B,$ je događaj koji se ostvario ako se ostvario događaj $A$ i događaj $B .$

Riješite sljedeće zadatke.

Kolekcija zadataka #2

Novčić bacamo dva puta. Dani su događaji $A = \{palo je točno jedno pismo\}$ i $B = \{palo je barem jedno pismo\} .$ Koji od navedenih Vennovih dijagrama prikazuje ta dva događaja?

Vennov dijagram prikazuje presjek događaja

null

Bacamo dvije kocke. Dani su događaji $A = \{na kockama su isti brojevi\}$ i $B = \{zbroj brojeva na kockama je 10\} .$

Presjek događaja $A \cap B$

događaj

C = \{(4, 6), (6, 4)\},

događaj

D = \{(5, 5)\} .

null

Bacamo novčić tri puta. Dani su događaji $A = \{nisu pala tri pisma ni tri glave\}$ i $B = \{pala su dva pisma i jedna glava\} .$ Presjek događaja $A \cap B$ je događaj $B .$

null

U vrećici je $5$ bijelih, $3$ crvene i $1$ crna kuglica. Iz vrećice nasumice izvlačimo $2$ kuglice. Dani su događaji $A = \{izvučena je točno jedna bijela kuglica\}$ i $B = \{izvučene su kuglice različitih boja\} .$ Koji je događaj presjek događaja $A \cap B ?$

A \cap B = \{nije izvučena nijedna crvena kuglica\}

A \cap B = \{izvučene su kuglice različitih boja\}

A \cap B = \{izvučene su bijela i crvena kuglica ili bijela i crna kuglica\}

null

Primjer 2.

Bacamo kocku jedanput. Dani su događaji $A = \{pao je djelitelj broja 15\}$ i $B = \{pao je paran broj\} .$ Odredimo $A \cap B$ i prikažimo ga Vennovim dijagramom.

$A = \{1, 3, 5\},$ $B = \{2, 4, 6\}$

Očito je $A \cap B = \emptyset$ .

Vennov dijagram prikazuje međusobno isključive događaje — Međusobno isključivi događaji

Za događaje $A$ i $B$ kažemo da se međusobno isključuju ako je $A \cap B = \emptyset .$ Skupovi $A$ i $B$ su disjunktni, događaji $A$ i $B$ se ne mogu istovremeno ostvariti.

Unija događaja

Primjer 3.

Bacamo jednu kocku. Pogledajmo događaje $A = \{pao je paran broj\}$ i $B = \{pao je broj manji od 4\} .$ Što je $A \cup B ?$

$A = \{2, 4, 6\},$ $B = \{1, 2, 3\}$

$A \cup B = \{1, 2, 3, 4, 6\}$

Vennov dijagram prikazuje uniju dvaju događaja — Unija dvaju događaja

Unija dvaju događaja $A \cup B,$ je događaj koji se ostvario ako se barem jedan od događaja $A$ ili $B$ ostvario.

Riješite zadatke.

Kolekcija zadataka #3

Nasumice biramo obitelji s dvoje djece. Dani su događaji $A = \{barem je jedno dijete dječak\},$ $B = \{djeca su različitog spola\}$ i $C = \{djeca su istoga spola\} .$ Koja je od navedenih tvrdnja istinita?

B \cup C = A

A \cup B = A

A \cup C = A

A \cup B = Ω

B \cup C = Ω

null

U kutiji se nalaze $4$ plave, $4$ crvene i $4$ zelene kuglice. Kuglice iste boje označene su brojevima od $1$ do $4 .$ Iz kutije se nasumice vadi jedna kuglica. Dani su događaji $C = \{izvučena je crvena kuglica\}$ i $B = \{izvučena je kuglica s brojem manjim od 3\} .$ Razvrstajte događaje u odgovarajuće skupove.

z 2

z 3

c 2

z 4

p 1

c 4

c 3

p 2

p 3

z 1

p 4

c 1

$C \cup B$

$\bar{C \cup B}$

null

Novčić bacamo tri puta. Dani su događaji $A = \{nije palo nijedno pismo\}$ i $B = \{nije pala nijedna glava\} .$ Čemu je jednako $A \cup B$ ?

A \cup B = \{palo je i pismo i glava\}

A \cup B = \{palo je barem jedno pismo\}

A \cup B = \{pala su tri pisma ili tri glave\}

null

6.2 Operacije s događajima

Na početku...