

Pogledajte animaciju pa razmislite o ovim pitanjima.
Je li tata platio matematički točno onoliko koliko je trebao, s obzirom na izloženu cijenu? Koji su mogući razlozi da je platio manje ili više?
Istražite običaje za kupovinu i prodaju na tržnicama u različitim zemljama. Cjenkanje je dio kulturoloških običaja nekih zemalja - potražite kojih.
Za uvježbavanje proporcionalnosti i obrnute proporcionalnosti predlažemo vam nekoliko zadataka koje možete samostalno riješiti u bilježnicu ili u nekom interaktivnom uređaju. Zadnjih je nekoliko zadataka za one koji žele znati više, ali svi ih možete pokušati riješiti. Nakon što riješite zadatke, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili zamolite da vam pomognu ako vam je neki zadatak težak.
Pojednostavnite omjere.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Pomnožite ili podijelite oba člana omjera istim brojem
Zračna udaljenost od Pule do Delnica iznosi oko
U kojem je mjerilu napravljena karta Hrvatske u atlasu ako je na njoj udaljenost između tih dvaju gradova izmjerena ravnalom jednaka
Učenici 7. c razreda jedne škole u Zagrebu pisali su prvi ispit znanja. Odličnih ocjena bilo je tri, vrlo dobrih šest, dobrih sedam, dovoljnih tri i dvije su ocjene bile nedovoljne. Učiteljica mora upisati u e-dnevnik omjer pozitivno ocijenjenih učenika u odnosu na ukupan broj učenika. Koji će omjer učiteljica upisati?
Omjer koji će učiteljica upisati jest
Dva fotografa Ivo i Pero izrađuju fotografije za jedan časopis. Ivo je napravio
fotografija, a Pero
fotografije. Izdavač im je platio ukupno
Koliko će od toga dobiti Ivo, a koliko Pero ako pravedno podijele zaradu?
Ivo će dobiti , a Pero .
Izračunajte nepoznati član razmjera ili proporcije
.
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Pomnožite vanjski član s vanjskim i unutarnji s unutarnjim.
Koliko je visok jablan čija je sjena duga
ako je istodobno sjena djevojčice visoke
koja stoji pokraj tog jablana duga
U kremu za bijelu pitu na mlijeka idu žlice brašna. Stavite li žlica brašna, koliko trebate mlijeka?
Na žlica brašna ide mlijeka.
Karta je napravljena u mjerilu Kolika je stvarna zračna udaljena između dvaju gradova ako su na karti njihove oznake udaljene ?
Stvarna zračna udaljenost između tih dvaju gradova jest
Odredite na geografskoj karti Hrvatske kolika je udaljenost od vašeg mjesta do nekog mjesta u koje biste željeli otputovati. Prema mjerilu te karte izračunajte njihovu stvarnu zračnu udaljenost.
Na mrežnoj stranici Udaljenosti među gradovima pronađite kolika je njihova cestovna udaljenost. Vozite li se koliko će vam vremena trebati da prijeđete tu udaljenost? Koliko bi vam vremena trebalo ako brzinu povećate za , a koliko ako brzinu smanjite za ?
Pokažite svoje rješenje drugom učeniku pa međusobno provjerite točnost postupka.
Nakon toga pronađite u atlasu neku kartu u drugom mjerilu, izmjerite udaljenosti među oznakama gradova koje ste odabrali na početku i izračunajte njihovu stvarnu zračnu udaljenost. Ako ste dobro mjerili i točno računali, trebali biste dobiti jednake rezultate kao i u prethodnom rješavanju.
Ivan trči brzinom od
i trči
minuta. Ako smanji brzinu na
, koliko će mu minuta trebati za jednaku udaljenost?
Pomoć:
Odredite koeficijent ili postavite razmjer obrnute proporcionalnosti.
U tvornici mobitela pripremaju se za isporuku. Mobitele mogu pakirati u tri vrste sanduka: srednji, veći i manji. Ako pakiraju u manje sanduke, trebat će im
sanduka, a u svakom će biti
mobitela.
Da bi se isplelo pletivo širine
na iglu treba navesti
očica.
Stroj za tiskanje novčanica otisne
novčanica za
sati i
minuta. Koliko novčanica otisne za
sati i
minuta.
Stroj za to vrijeme otisne novčanica.
berača obralo bi nasade malina za
dana. Zbog loše vremenske prognoze, nakon tri dana odlučeno je da maline moraju biti obrane za ukupno
dana. Koliko još berača nedostaje da posao bude završen na vrijeme?
Nedostaje još
berača.
Izračunajte.
Noa je na skijanju u Sloveniji. Sa sobom nosi
eura džeparca. Ako
euro vrijedi
kuna, koliko kuna džeparca Noa nosi sa sobom?
Pomoć:
Pomnožite količinu eura sa
Jesu li valute proporcionalne veličine?
Ako je Noa
dana na zimovanju i planira džeparac ravnomjerno podijeliti po danima, koliko dnevno džeparca može potrošiti?
Luna je pronašla recept za izradu čokoladnog kolača za
osoba.
Za biskvit je potrebno:
Za kremu je potrebno:
Za čokoladnu glazuru potrebno je:
Luna planira napraviti kolač za osoba. Tada joj je potrebno:
| Čokolada za kuhanje | |
| Slatko vrhnje | |
| Naribana narančina korica | |
| Čokolada za kuhanje (za glazuru) | |
| Maslac (za glazuru) |
Pomoć:
Sve su veličine u zadatku proporcionalne.
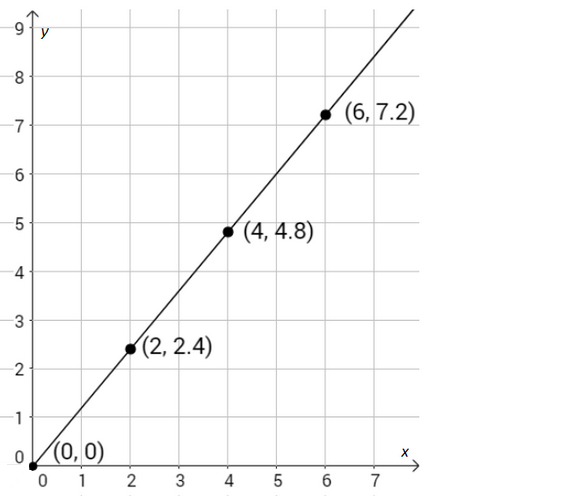
Kakve su veličine količina jaja i iznos koji je potrebno platiti za određenu količinu jaja?
Iz grafa očitajte cijenu.
| jaja | |
| jaja | |
| jaja |
Pomoć:
Očitajte uređene parove s grafa, količinu jaja s osi
cijenu s osi
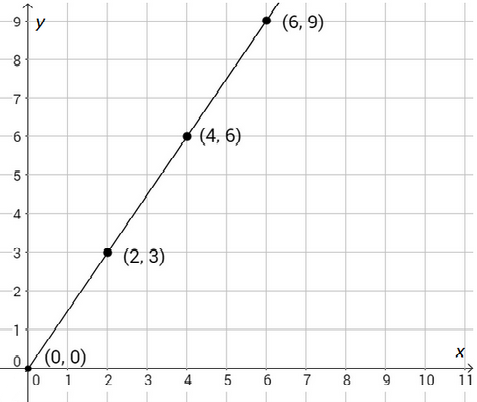
Na osi je količina krumpira u na osi je cijena krumpira u
Količina krumpira i cijena koju za nju moramo platiti
Iz grafa iščitajte:
Za
krumpira potrebno je platiti , dok je za
krumpira potrebno platiti .
Pomoć:
Očitajte s grafa uređene parove, količinu s osi
cijenu s osi
Površina pravokutnika je
Izračunajmo moguće duljine stranica tog pravokutnika ako znamo da su duljine tih stranica prirodni brojevi.
Duljine stranica toga pravokutnika mogu biti: i i te i Prisjetimo se da je formula za površinu pravokutnika:
Opseg jednakostraničnog trokuta jest Izračunajte duljinu stranice jednakostraničnog trokuta šest puta većeg opsega.
Duljina stranice većeg jednakostraničnog trokuta jest Prisjetimo se da je formula za opseg jednakostraničnog trokuta:
radnika popravlja željezničku prugu radeći
dana po
sati dnevno. Ako bi se zaposlilo
radnika koji bi radili
dana, koliko bi sati dnevno oni morali raditi da poprave tu prugu, ako im je ista učinkovitost?
Ako obračunamo ukupne radne sate u oba slučaja, radnika radit će ukupno sata. Zanima nas koliko bi sati isti posao s istom učinkovitosti radilo radnika. Oni će raditi dnevno sati, a ukupno sati. Kada postavimo razmjer u obrnutu proporcionalnost, vidimo da će radnika dnevno raditi sati.
bagera kopa temelje trgovačkog centra radeći
dana po
sati. Ako bi unajmili još
bagera i svi bi bageri zajedno dnevno radili
sati, koliko bi dana trebali raditi?
Ako obračunamo ukupne radne sate u oba slučaja, bagera ukupno će raditi sata.Zanima nas koliko bi sati isti posao s istom učinkovitosti radilo bagera koji će u dana odraditi sati. Kada postavimo razmjer u obrnutu proporcionalnost, vidimo da će bagera raditi dana.
Bruna preuređuje svoju sobu. Želi na jedan zid staviti dekorativnu traku širine U knjizi o uređenju prostorija pročitala je da sredina trake treba dijeliti zid od stropa prema podu u omjeru Zid Brunine sobe visok je
Koliko treba odmjeriti od stropa da bi traku stavila na pravo mjesto?
Bruna planira donji dio zida obojiti u ružičasto, a gornji dio u bijelo.
U dogovoru s roditeljima, osmislite kako biste vi obojili svoju sobu. Izmjerite potrebne veličine. Saznajte cijene i količine boje koju trebate. Pozovite prijatelje, osvježite svoju sobu i pritom se dobro zabavite.
Zadaci s proporcionalnim i obrnuto proporcionalnim veličinama često se pojavljuju na Državnoj maturi pa predlažemo da pogledate i ove zadatke:
Poigrajte se na kraju s preračunavanjem mjernih jedinica koje su također proporcionalne veličine.