3.7 Složenije nejednadžbe

Sustav kvadratnih nejednadžbi

Jednako kao i kod linearnih jednadžbi i složenije kvadratne nejednadžbe svest će se na rješavanje sustava kvadratnih nejednadžbi. Pogledajmo kako se rješavaju sustavi kvadratnih nejednadžbi.

Primjer 1.

Riješimo sustav kvadratnih nejednadžbi:

$\left\{\begin{array}{l}-x^2+5x<4\\ x^2>4\end{array}\right..$

Riješiti sustav nejednadžbi znači pronaći sve brojeve koji zadovoljavaju i jednu i drugu nejednadžbu. Da bismo odredili rješenje sustava, rješit ćemo svaku nejednadžbu zasebno te nakon toga odrediti presjek obaju rješenja.

Nejednadžba $-x^2+5x<4$ može se napisati u obliku $-x^2+5x-4<0.$ Odredimo nultočke kvadratne funkcije $f\left(x\right)=-x^2+5x-4.$ Rješavajući kvadratnu jednadžbu dobivamo $x_1=1,x_2=4.$ Grafički predočimo funkciju i očitajmo rješenje.

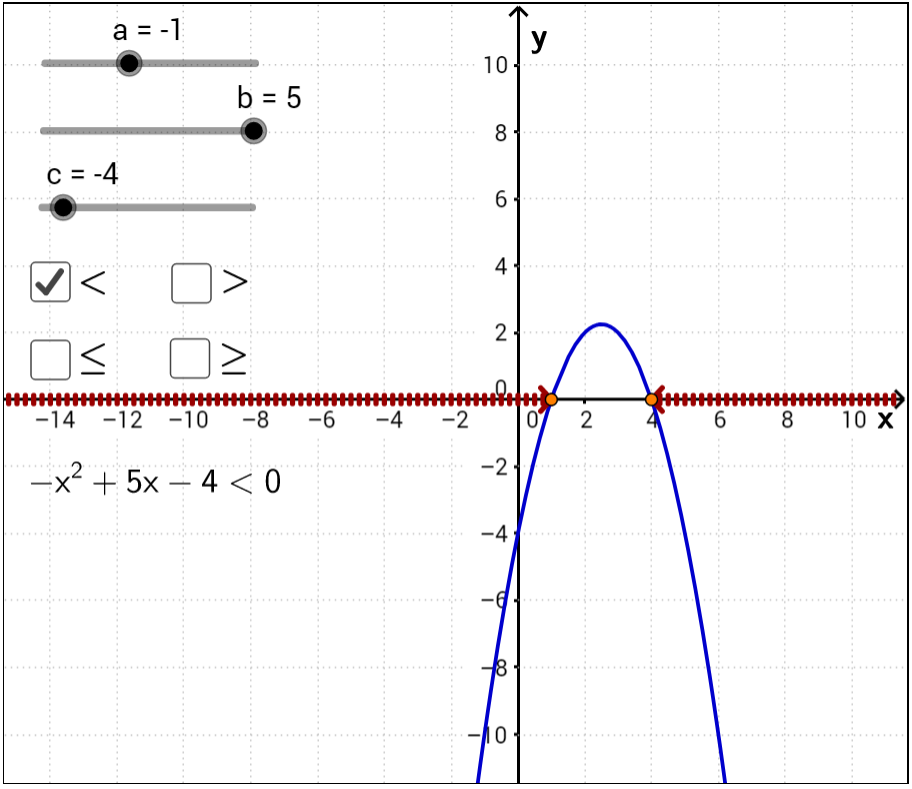
Rješenje prve nejednadžbe je interval $⟨-\infty ,1⟩\cup ⟨4,+\infty ⟩.$

Nejednadžba $x^2>4$ je ekvivalentna nejednadžbi $x^2-4>0,$ čije nultočke su $x_1=-2,x_2=2.$ Grafički predočimo funkciju $f\left(x\right)=x^2-4$ i očitajmo rješenje.

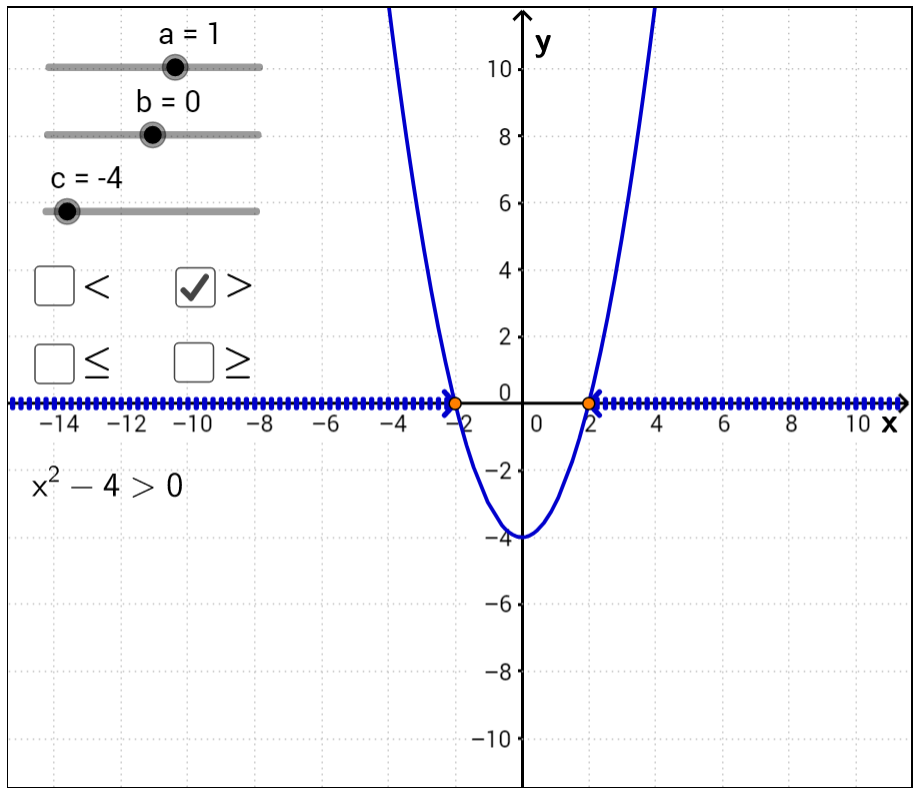
Rješenje druge nejednadžbe je interval $<-\infty ,-2>\cup <2,+\infty >.$

Presjek tih dvaju rješenja možemo prikazati na pravcu.

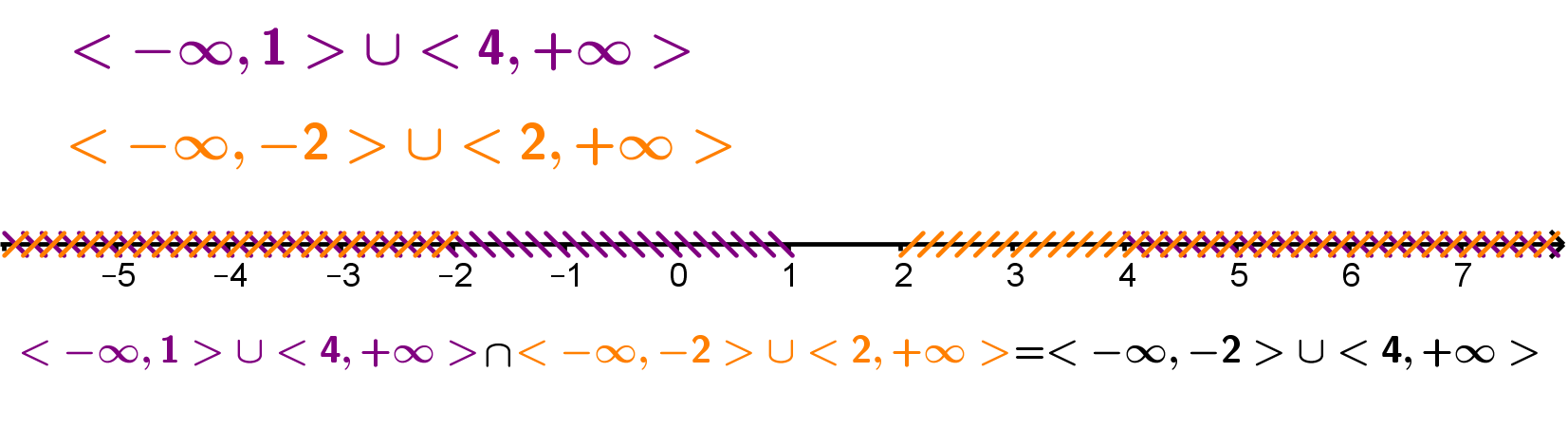
Konačno rješenje je presjek rješenja iz prvoga i drugoga slučaja $⟨-\infty ,-2⟩\cup ⟨4,+\infty ⟩.$

Kolekcija zadataka 1

Zadatak 1.

Riješite sustav nejednadžbi.

$\left\{\begin{array}{l}2x^2-x-3\le 0\\ x^2+3x-4>0\end{array}\right.$

Kao pomoć možete upotrijebiti predložak za rješavanje kvadratnih nejednadžbi.

Rješenje

$x\in \left.⟨1,\frac{3}{2}\right]$  ​

---

Zadatak 2.

Riješite sustav.

$\left\{\begin{array}{l}{x}^2+x+1\le 0\\ x^2+2x+4\ge 0\end{array}\right.$

Kao pomoć možete upotrijebiti GeoGebrin predložak iz prethodnog zadatka kako biste riješili kvadratne nejednadžbe.

Rješenje

Rješenje prve nejednadžbe je $\varnothing ,$ a rješenje druge nejednadžbe je cijeli skup $\mathbf{R}.$ Njihov je presjek $\varnothing$ pa je to traženo rješenje.

---

Zatvori

Kutak za znatiželjne

Koliko cjelobrojnih rješenja ima sustav nejednadžbi:

$\left\{\begin{array}{l}|x^2-5x+4|\ge 2\\ \left|x\right|<2017\end{array}\right..$

Taj se zadatak pojavio na školskom natjecanju iz Matematike 2017. godine u B kategoriji.

Složenije nejednadžbe

Primjer 2.

Složenije nejednadžbe svode se na sustave nejednadžbi. Pogledajmo primjer.

Riješimo nejednadžbu: $\frac{x^2-3x}{x^2-3x+2}\le 0.$

Razlomak je negativan ako su brojnik i nazivnik suprotnih predznaka.

Zato tu nejednadžbu možemo raspisati na dva slučaja:

• Prvi slučaj $x^2-3x\ge 0i{x}^2-3x+2<0$ 
• Drugi slučaj $x^2-3x\le 0i{x}^2-3x+2>0.$
  

U prvom je slučaju rješenje prve nejednadžbe $\left.⟨-\infty ,0\right]\cup \left[3,+\infty \right.⟩,$ a druge $⟨1,2⟩.$ Presjek tih dvaju rješenja je prazan skup.

U drugom je slučaju rješenje prve nejednadžbe $\left[0,3\right],$ a druge $⟨-\infty ,1⟩\cup ⟨2,+\infty ⟩.$

Presjek tih dvaju rješenja je $\left[0,1\right.⟩\cup \left.⟨2,3\right].$

Konačno rješenje dobijemo kao uniju rješenja iz prvoga i drugoga slučaja: $\left[0,1\right.⟩\cup \left.⟨2,3\right].$

Napomena: Kao pomoć pri rješavanju kvadratnih nejednadžbi možete upotrijebiti GeoGebrin predložak iz prvog zadatka.

Rješavanje složenijih jednadžbi raspisivanjem na slučajeve prilično je zahtjevno. Treba biti osobito pažljiv ‒ kad određujemo uniju, a kad presjek rješenja. Jednostavniji način rješavanja složenih nejednadžbi je s pomoću testiranja točaka intervala. Pogledajmo na našem primjeru.

Ako faktoriziramo našu nejednadžbu, dobivamo:

$\frac{x(x-3)}{(x-1)(x-2)}\le 0.$

Tzv. kritične točke (točke u kojima se mijenjaju predzanci linearnih članova) dobijemo izjednačavanjem svakog od linearnih faktora s $0.$

Kritične točke:

$x=0\Rightarrow x_1=0$

$x-3=0\Rightarrow x_2=3$

$x-1=0\Rightarrow x_3=0$

$x-2=0\Rightarrow x_4=2.$

Ako podijelimo skup realnih brojeva na podintervale i smjestimo u tablicu, dobit ćemo:

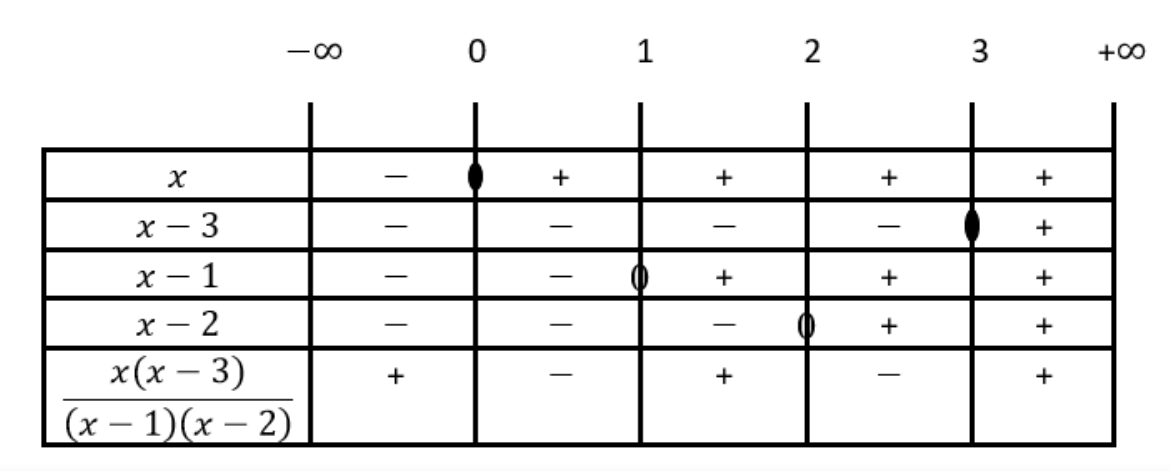
Rješenje možemo pročitati u posljednjem retku tablice. Kako se u nejednadžbi traže intervali u kojima je vrijednost manja od $0$ ili jednaka $0,$ rješenje je $\left[0,1\right.⟩\cup \left.⟨2,3\right].$

Primjer 3.

Rješimo nejednadžbu. ​

$\frac{2x}{x-1}\le \frac{x}{x-2}$

Najjednostavnije bi bilo kad bismo nejednadžbu mogli pomnožiti s nazivnicima i svesti na jednu nejednadžbu. Nažalost, to nije moguće bez dodatnih uvjeta. Prisjeti se prvog primjera!

Ako prebacimo sve na lijevu stranu, dobivamo ​ $\frac{2x}{x-1}-\frac{x}{x-2}\le 0.$ Svođenje na zajednički nazivnik i sređivanje izraza daje $\frac{x^2-3x}{x^2-3x+2}\le 0.$ Dobili smo nejednadžbu koju smo riješili u prethodnom primjeru.

Zadatak 3.

Riješite nejednadžbu: ​ $\frac{x^2-2}{x^2-x-2}\ge 1.$

Postupak rješavanja složenijih nejednadžbi:

1. Prebacite sve članove na lijevu stranu, tako da s desne strane znaka nejednakosti ostane $0.$
2. Sredite izraz na lijevoj strani (zbrojite, faktorizirajte i skratite ako možete), tako da dobijete samo jedan razlomak.
3. Nađite kritične točke tako da svaki linearni ili kvadratni član izjednačite s $0.$
4. Napravite analizu predznaka u tablici. Intervale određuju kritične točke, a predznake dobijemo uvrštavanjem nekog broja iz intervala u linearni, odnosno kvadratni član.
5. Upotrijebite svojstvo množenja pozitivnih i negativnih brojeva da biste dobili predznak traženog izraza u posljednjem redu tablice.
   
6. Odredite rješenje isčitavajući predznak traženog izraza. Ako se u nejednadžbi traži manje ili manje jednako $0,$ rješenje su intervali u kojima je znak $-,$ povezani znakom unija, a ako se u nejednadžbi traži veće ili veće jednako, rješenja su intervali u kojima je znak $+,$ povezani znakom unija.
   

Za uvježbavanje rješavanja složenijih nejednadžbi možete upotrijebiti generator zadataka. Rješenje provjeravajte pritiskom na tipku RJEŠENJE, a novi zadatak dobit ćete pritiskom na tipku NOVI ZADATAK.