Aktivnosti za samostalno učenje

Parabole oko nas

Projekt

Ne moramo ići u Sydney, San Francico, Pariz ili daleku Australiju (a možda bismo i mogli) da bismo pronašli parabole. One su i tu negdje oko nas, samo se treba osvrnuti.

Organizirajte tim i krenite u potragu za parabolama koje ćete moći izmjeriti te pronaći kvadratnu funkciju koja najbolje odgovara tom obliku.

Predlažemo sljedeći tijek aktivnosti:

1. ​Pronađite i snimite više primjera „parabola”. Možete napraviti i „selfie” s parabolom kako bi se vidjelo da su to doista vaše slike.
2. Odaberite sliku čije dimenzije u stvarnosti najlakše možete izmjeriti ili dobiti podatke o njoj (širina parabole – nultočke; visina parabole – tjeme; izmjeriti neke druge točke kojima ćete upisati koordinate; možete pronaći podatke o nekoj građevini, skulpturi, portalu, vodoskoku i sl. te ih iskoristiti za definiranje točaka na paraboli).
3. Nakon što ste dobili minimalno tri podatka, počnite računati parabolu. Odaberite u koju jednadžbu parabole ćete uvrštavati podatke: $y=a{x}^2+bx+c,$ $y=a{\left(x-x_0\right)}^2+y_0$ ili $y=a\left(x-x_1\right)\left(x-x_2\right).$ Nacrtajte parabolu na papiru (prilagodite omjere) i napišite joj jednadžbu.
4. Vratite se u školske klupe (ili kod nekoga tko ima volje napraviti palačinke – pa zaslužili ste), smjestite sliku u koordinatni sustav u nekom programu dinamične geometrije (npr. GGB), nacrtajte parabolu kroz točke koje ste prethodno izračunali te prilagodite sliku paraboli.
   
5. Razgovarajte o dobivenim rezultatima. Ako su se parabole donekle poklopile, zašto se to dogodilo (tko je zaslužan), ili ako postoji pogreška, zbog čega se dogodila (pogreška u računu ili možda ipak taj oblik koji ste odabrali nije oblik parabole nego nešto slično).
   

6. Napravite pregled tijeka svojih aktivnosti (video, prezentacija, plakat) te prezentirajte to u razredu.
   

Pogledajte kako su učenici Elektrotehničke i prometne škole iz Osijeka izmjerili Dravski most.

Praktična vježba

Kako još možemo doći do jednadžbe parabole nekog oblika u prirodi ili utvrditi ima li on uopće oblik parabole? S pomoću GeoGebre. Pogledajte u nastavku postupak dobivanja jednadžbe parabole.

Koraci koji prate animaciju u nastavku:

• ​otvorite GeoGebru (koristite se Grafičkim prikazom) ili postojeći GeoGebrinu interakciju u nastavku za rad
  
• umetnite pripremljenu sliku (klik na alat /ikonu Slika → Odaberi datoteku ili Uređivanje → Umetni sliku iz → Datoteka)
• pomaknete je (mišem) na mjesto gdje vam najbolje odgovara za crtanje parabole preko nje; dimenzije mijenjate pomicanjem točaka kojima je definirana
• kad ste ju namjestili, sakrijete točke (pozicionirate se na točku → desni klik mišem → Pokaži objekt)
• definirate klizače: $a$, $b$ i $c$ tako da najprije kliknete na koordinatni sustav gdje želite da budu pozicionirani (klik na alat/ikona Klizač → definirate interval npr. od $-10$ do $10$ te korak povećanja $0.01$)
• u polje za unos (upotrijebite virtualnu tipkovnicu za zapis kvadrata) upišite jednadžbu parabole: $y=a{x}^2+bx+c$
  
• namještajte dok ne dobijete željeni oblik
  
• možete odabirom Svojstva objekta (slike) u kartici Osnovno uključiti opciju Pozadinska slika.
  

Sada pokušajte sami.

Različiti zapisi kvadratne funkcije

Zadatci za najupornije

Zadatak 1.

Riješite nejednadžbu:

$\begin{array}{l}\frac{2x-25}{2\left(x^2+2x-3\right)}+\frac{2x+11}{2\left(x^2-1\right)}>\frac{1}{x+3}\end{array}.$

Povezani sadržaji

Zadan je polinom $P\left(x\right)=2x^3-x^2-14x+7.$ Provjerite je li $\frac{1}{2}$ jedna nultočka tog polinoma i rastavite ga na linearne faktore.

Kutak za znatiželjne

Riješite u skupu cijelih brojeva sustav nejednadžbi.

$\begin{array}{l}y-\left|x^2-2x\right|+\frac{1}{2}>0\\ y+\left|x-1\right|<2\end{array}$

Nađite presjek dviju pripadajućih jednadžbi.

Uputa: riješite zadatak grafički (primijenite metodu pomaka grafa).

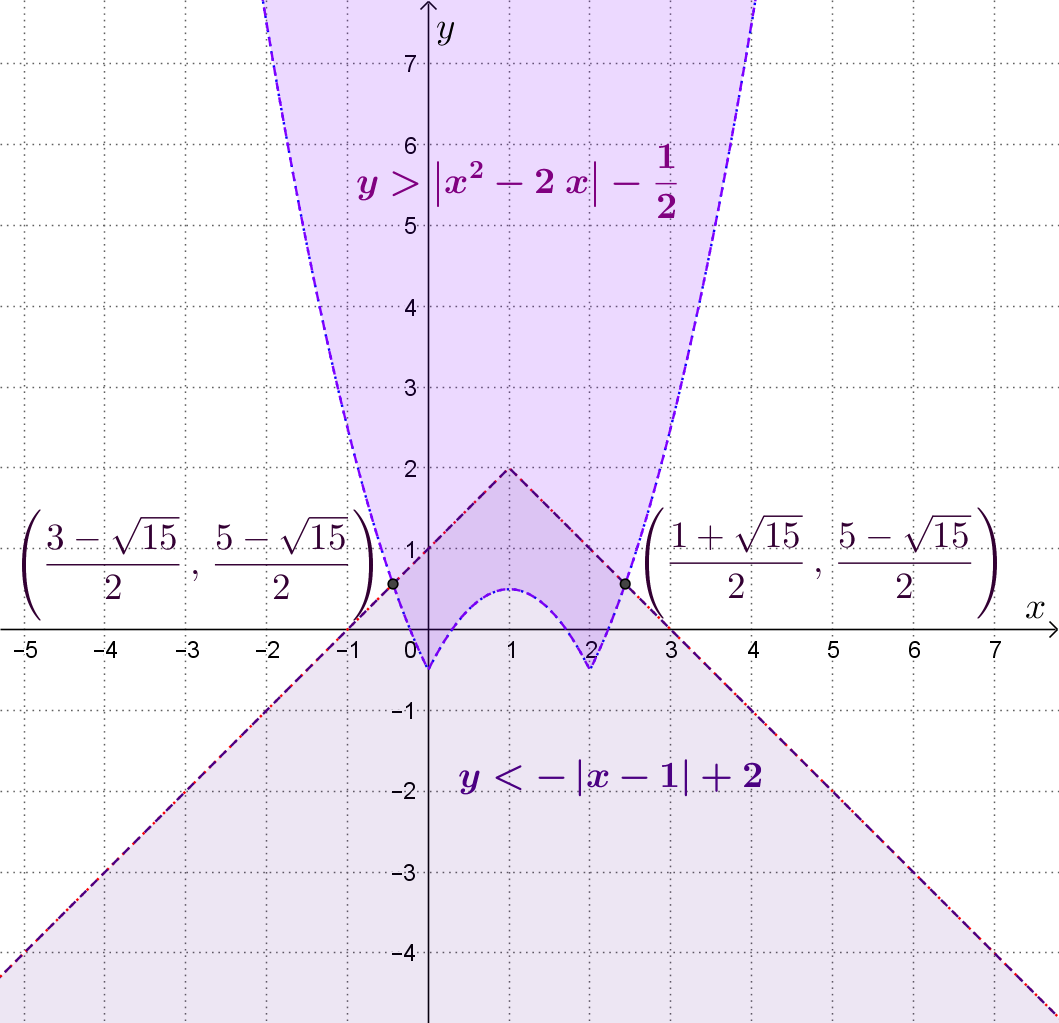
Nacrtajte: $\begin{array}{l}y=\left|x^2-2x\right|-\frac{1}{2}\\ y=-\left|x-1\right|+2.\end{array}$

Postupak crtanja/dobivanja rješenja:

• parabolu $y=\left|x^2-2x\right|=\left|x\left(x-2\right)\right|$ pomaknemo za $\frac{1}{2}$ dolje
  
• iz početne nejednadžbe dobijemo ​ $y>-\frac{1}{2}$ (što se moglo odmah naslutiti zbog pomaka po osi $y$)
• apsolutnu vrijednost $y=-\left|x\right|$ pomaknemo za $1$ udesno i za $2$ gore
•  iz početne nejednadžbe dobijemo ​ $y<2$ (što se moglo naslutiti odmah zbog pomaka za $2$)
• potražimo za koje $x$-eve je $-\frac{1}{2}<y<2$
  
• kako se traže cjelobrojna rješenja, lako se iz grafa vidi da je rješenje $0$ i $2.$
  

Savjet:

Upotrijebite GeoGebrin predložak za crtanje parabole (imate u tekstu iznad). U polje za unos upišite (ne)jednadžbe (GeoGebra podržava i nejednadžbe). Za upis znaka apsolutno i kvadrat upotrijebite virtualnu tipkovnicu u donjem lijevom kutu. Prema potrebi, zumirajte grafički prikaz. Iz grafa pročitajte cjelobrojna rješenja presjeka na osi $x.$

Riječi, riječi, riječi...

Povezani sadržaji

Moment sile je umnožak sile i njezine najkraće udaljenosti do točke u kojoj se moment računa.
Ako sila čiji moment računamo izaziva rotaciju u smjeru kazaljke na satu, moment ima negativan predznak. U suprotnom je pozitivan.

Na slici je prikazano opterećenje grede na dva oslonca te djelovanje momenta savijanja na gredu.

Istražite dodatno značenje pojmova: moment sile, greda, težina i savijanje.

Više o funkciji momenta savijanja doznajte od nastavnika Fizike.

Kolekcija zadataka 2

Zadatak 4.

Greda mase $m$ i duljine $L$ oslonjena je svojim krajevima na oslonce i opterećena je vlastitom težinom $mg.$ Funkcija momenta savijanja dana je formulom $M\left(x\right)=-\frac{mg}{2L}·x^2+\frac{mg}{2}·x,$ gdje je $x$ udaljenost od lijevog oslonca grede. Odredite:​

1. maksimalni moment savijanja
2. moment savijanja u točki udaljenoj $\frac{1}{3}L$ od lijevog oslonca (oslonci su nultočke funkcije, iz zadane je funkcije vidljivo da je graf funkcije momenta okrenut prema dolje i prolazi kroz ishodište).

Rješenje

1. $M_{max}=\frac{mg}{8L}$
   
2. $M\left(\frac{1}{3}L\right)=\frac{mgL}{9}$
   

---

Zadatak 5.

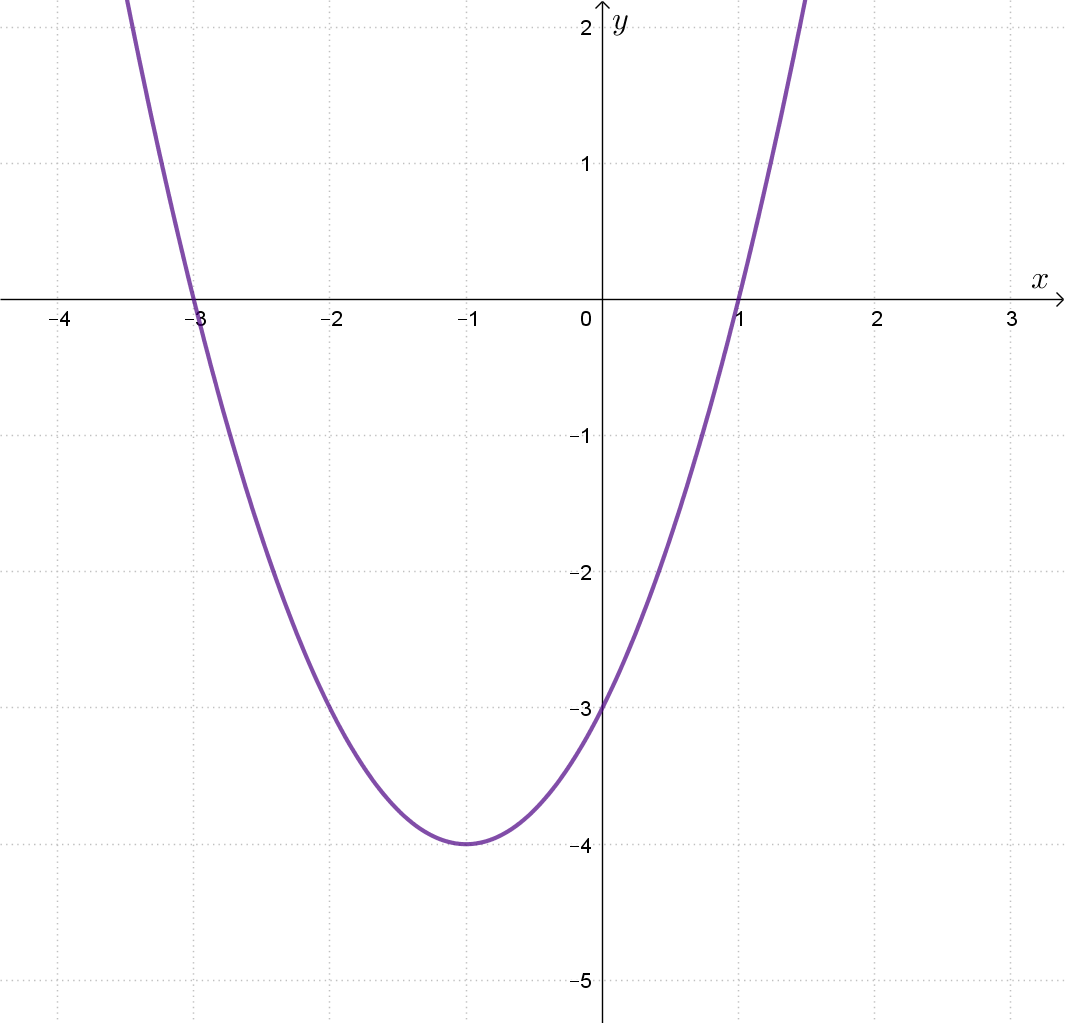
Za koje je vrijednosti parametra $m$ funkcija ​ $y=m{x}^2+2\left(m+2\right)x+2m+4$ negativna za svaki $x?$

Rješenje

Ovaj zadatak možete riješiti s pomoću interakcije. Napravite brojač za $m,$ upišite u polje za unos jednadžbu parabole te mijenjajte $m.$ Rješenje:  $m<-2.$

---

Zatvori