Matematika 8 - 8.8 Ostale prizme

Na početku...

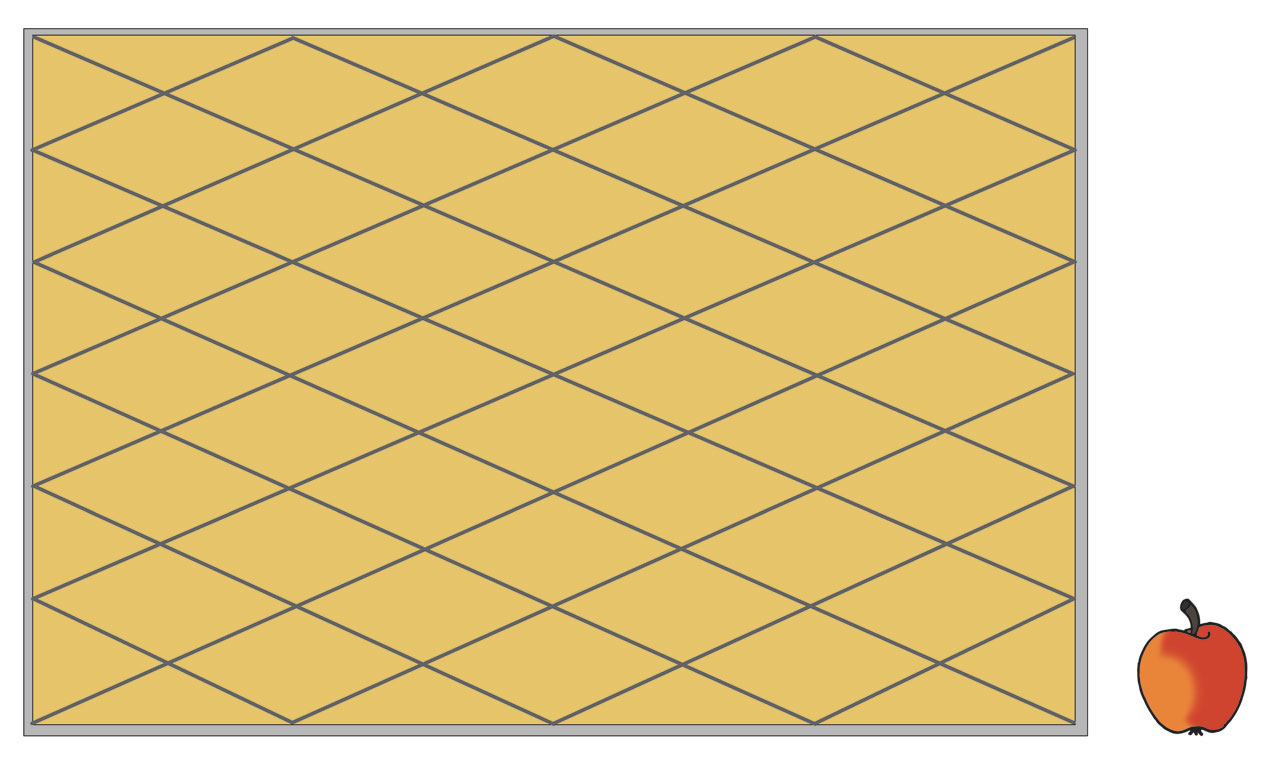
Slika prikazuje pitu od jabuke izrezane na prizme čija je baza romb. Ostatici kod ruba kolača sačinjeni su od prizmi čije su baze jednakostranični ili jednakokračni trokuti.

Ivana je ispekla pitu od jabuka u limu duljine $36 cm$ i širine $24 cm .$ Visina je pečene pite bila $6 cm .$ Odlučila je pitu izrezati kao što je prikazano na slici. Kakva su oblika izrezani dijelovi? Koliki je volumen pojedinog dijela?

Slika prikazuje oblike izrezanih kolača (prizme čije su baze redom rombovi, jednakokračni torkuti i jednakostranični trokuti).

Izrezane komade kolača možemo shvatiti kao uspravne prizme visine $6 cm,$ kojima su baze rombovi odnosno jednakokračni trokuti. Prema slici zaključujemo da je duljina veće dijagonale romba (i osnovice tupokutnoga jednakokračnog trokuta) jednaka $36 : 4 = 9 cm,$ dok je duljina manje dijagionale romba (i osnovice šiljastokutnoga jednakokračnog trokuta) jednaka $24 : 6 = 4 cm .$

U primjerima i zadatcima koji slijede naučit ćete kako izračunati volumen Ivaninih kolača!

Trostrane prizme

Promotrite mreže različitih trostranih prizmi.

Baza pravokutni trokut

Primjer 1.

Promotrimo mrežu uspravne prizme kojoj je baza pravokutni trokut s katetama duljina $a$ i $b$ te hipotenuzom duljine $c,$ pri čemu je $h$ visina prizme.

Mreža se sastoji od dvaju sukladnih pravokutnih trokuta i triju pravokutnika koji imaju jednu stranicu duljine $h$ .

Površinu baze (pravokutnog trokuta s katetama duljina $a$ i $b$ ) računamo po formuli $B = \frac{1}{2} a b .$ Površinu pobočja te prizme računamo kao zbroj površina triju pravokutnika sa stranicama duljina $a$ i $h,$ $b$ i $h$ te $c$ i $h,$ tj.

$P = a h + b h + c h .$

Slika prikazuje površine strana prizme kojoj je baza pravokutni trokut.

Za računanje oplošja i volumena takve prizme primijenit ćemo opće formule $O = 2 B + P$ i $V = B h .$

Kolekcija zadataka 1

Zadatak 1.

Baza je trostrane prizme pravokutni trokut s katetama duljina $48 mm$ i $5.5 cm,$ a visina je te prizme $8 cm .$ Izračunajte oplošje i volumen te prizme.

Slika prikaze dijelove mreže prizme kojoj je baza pravokutan trokut (bazu i pobočje).

Površina se pravokutnog trokuta s katetama duljina $a$ i $b$ računa prema formuli $B = \frac{1}{2} a b$ pa uvrštavanjem dobivamo $B = \frac{1}{2} \cdot 48 \cdot 55 = 24 \cdot 55 = 1 320 {mm}^{2} .$

Za računanje površine pobočja potrebna je duljina hipotenuze pravokutnog trokuta. Primjenom Pitagorina poučka dobivamo da je $c^{2} = a^{2} + b^{2} = 48^{2} + 55^{2} = 2 304 + 3 025 = 5 329$ pa je $c = \sqrt{5 329} = 73 mm .$

Uvrštavanjem podataka u izraz za računanje površine pobočja dobiva se $P = a h + b h + c h = (a + b + c) h = (48 + 55 + 73) \cdot 80 = 176 \cdot 80 = 14 080 {mm}^{2} .$

Oplošje je te prizme $O = 2 B + P = 2 \cdot 1 320 + 14 080 = 16 720 {mm}^{2},$ a volumen $V = B h = 1 320 \cdot 80 = 105 600 {mm}^{3} .$

Zadatak 2.

Baza je trostrane prizme pravokutni trokut s hipotenuzom duljine

65 mm

i katetom duljine

56 mm,

a volumen je te prizme

90.552 {cm}^{3} .

Duljina je druge katete te prizme

mm

,

površina je baze

{mm}^{2},

duljina je visine prizme

mm

, površina je pobočja

{mm}^{2},

a oplošje je

{mm}^{2} .

null

Zatvori

Baza jednakokračni trokut

Primjer 2.

Promotrimo mrežu uspravne prizme kojoj je baza jednakokračni trokut s osnovicom duljine $a$ i krakom duljine $b$ , pri čemu je $h$ visina prizme.

Slika prikazuje prizmu i mrežu trostrane prizme kojoj je baza jednakokračan trokut.

Mreža se sastoji od dvaju sukladnih jednakokračnih trokuta i triju pravokutnika koji imaju jednu stranicu duljine $h$ .

Površinu baze (jednakokračnog trokuta s osnovicom duljine $a$ i visinom na osnovicu duljine $v$ ) računamo po formuli $B = \frac{1}{2} a v .$ Površinu pobočja te prizme računamo kao zbroj površina triju pravokutnika, jednoga sa stranicama duljina $a$ i $h$ te dvaju sa stranicama duljina $b$ i $h$ , tj. $P = a h + 2 b h .$

Slika prikazje površine strana prizme kojoj je baza jednakokračni trokut.

Za računanje oplošja i volumena takve prizme primijenit ćemo opće formule $O = 2 B + P$ i $V = B h .$

Kolekcija zadataka 2

Zadatak 3.

Baza je upravne prizme jednakokračni trokut s osnovicom duljine $32 cm$ i krakom duljine $34 cm .$ Visina je te prizme $20 cm .$ Izračunajte oplošje i volumen te prizme.

Slika prikazuje dijelove mreže prizme kojoj je baza jednakokračni trokut.

Primjenom Pitagorina poučka prvo računamo visinu baze $v^{2} = b^{2} - {(\frac{a}{2})}^{2} = 34^{2} - 16^{2} = 900,$ tj. $v = \sqrt{900} = 30 cm$ i zato je površina baze jednaka $B = \frac{1}{2} a v = \frac{1}{2} \cdot 32 \cdot 30 = 16 \cdot 30 = 480 {cm}^{2} .$ Volumen je te prizme $V = B h = 480 \cdot 20 = 9 600 {cm}^{3} .$

Površina je pobočja te prizme $P = a h + 2 b h = (a + 2 b) h = (32 + 2 \cdot 34) \cdot 20 = 100 \cdot 20 = 2 000 {cm}^{2},$ a oplošje je $O = 2 B + P = 2 \cdot 480 + 2 000 = 2 960 {cm}^{2} .$

Zadatak 4.

Slika prikazuje prizmu kojoj je baza jednakokračni trokut s upisanom formulama za površinu pojedinih strana.

Duljina je osnovice jednakokračnog trokuta jednaka $4 cm,$ a duljina visine na osnovicu $4.5 cm .$ Taj je trokut baza uspravne prizme čija je visina $6 cm .$ Koliki je volumen te prizme?

$51 {cm}^{3}$

$108 {cm}^{3}$

$216 cm$

$54 {cm}^{3}$

null

null
Baza je uspravne prizme jednakokračni trokut s osnovicom duljine $0.9 dm$ i visinom na osnovicu duljine $2 cm .$ Visina je te prizme $60 mm .$ Volumen te prizme iznosi ${mm}^{3} .$

Pomoć:

null

Baza je uspravne prizme jednakokračni trokut površine $2.4 {dm}^{2},$ a duljina je visine na osnovicu tog trokuta $24 cm .$ Oplošje je te prizme $1 344 {cm}^{2}$ . Spoji parove.

$a =$	$20 cm$
$v =$	$864 {cm}^{2}$
$P =$	$26 cm$
$V =$	$2880 {cm}^{3}$

null

Zatvori

Četverostrane prizme

Promotrite mreže raznih četverostranih prizmi.

Baza romb

Primjer 3.

Promotrimo mrežu uspravne prizme kojoj je baza romb sa stranicom duljine $a$ i dijagonalama duljina $e$ i $f,$ pri čemu je $h$ visina prizme.

Mreža se sastoji od dvaju sukladnih rombova i četiriju sukladnih pravokutnika sa stranicama duljina $a$ i $h$ .

Površinu baze (romba sa stranicom duljine $a$ i dijagonalama duljine $e$ i $f$ ) računamo po formuli $B = \frac{1}{2} e f .$ Površinu pobočja te prizme računamo kao zbroj površina četiriju pravokutnika sa stranicama duljina $a$ i $h,$ tj. kao $P = 4 a h .$

Slika prikazuje mrežu prizme kojoj je baza romb s upisanim formulama za površinu strana.

Kolekcija zadataka 3

Zadatak 5.

Baza je četverostrane prizme romb s dijagonalama duljina $28.8 cm$ i $8.4 dm .$ Koliko je oplošje te prizme ako je njezin volumen $30.24 {dm}^{3} ?$

Slika prikazuje dijelove mreže prizme čija je baza romb.

Površina je baze te prizme $B = \frac{1}{2} \cdot 28.8 \cdot 84 = 14.4 \cdot 84 = 1 209.6 {cm}^{2}$ pa na temelju poznate površine baze i volumena prizme slijedi da je visina prizme $h = 30 240 : 1 209.6 = 25 cm .$ Duljinu stranice romba nalazimo primjenom Pitagorina poučka pa iz $a^{2} = {(\frac{e}{2})}^{2} + {(\frac{f}{2})}^{2} = {14.4}^{2} + 42^{2} = 1 971.36$ slijedi da je $a = \sqrt{1 971.36} = 44.4 cm .$

Površina je pobočja jednaka $P = 4 a h = 4 \cdot 44.4 \cdot 25 = 4 440 {cm}^{2},$ a oplošje je te prizme $O = 2 B + P = 2 \cdot 1 209.6 + 4 440 = 2 419.2 + 4 440 = 6 859.2 {cm}^{2} .$

Zadatak 6.

Slika prikazuje mrežu prizme kojoj je baza romb.

Duljine su dijagonala romba $9 cm$ i $4 cm .$ Taj je romb baza uspravne prizme čija je visina $6 cm .$ Koliki je volumen te prizme?

$216 {cm}^{3}$

$108 {cm}^{3}$

$78 {cm}^{3}$

$39 {cm}^{3}$

null

null
Baza je uspravne prizme romb opsega $5.2 dm .$ Duljina je visine te prizme $5 cm,$ a duljina jedne dijagonale baze iznosi $24 cm .$ Oplošje je te prizme ${cm}^{2},$ a volumen joj je ${cm}^{3} .$

null

null

Zatvori

Baza jednakokračni trapez

Primjer 4.

Promotrimo mrežu uspravne prizme kojoj je baza jednakokračni trapez s osnovicama $a$ i $c,$ krakovima duljine $b$ i visinom baze duljine $v,$ pri čemu je $h$ visina prizme.

Mreža se sastoji od dvaju sukladnih jednakokračnih trapeza i četiriju pravokutnika (od kojih su dva međusobno sukadna) i svi pravokutnici imaju jednu stranicu duljine $h$ .

Površinu baze (jednakokračnog trapeza s osnovicama duljine $a$ i $c,$ krakovima duljine $b,$ visinom baze duljine $v$ ) računamo po formuli $B = \frac{a + c}{2} \cdot v .$ Površinu pobočja te prizme računamo kao zbroj površina četiriju pravokutnika sa stranicama duljina $a$ i $h$ tj. kao $P = a h + 2 b h + c h,$ odnosno $P = (a + 2 b + c) \cdot h .$

Slika prikazuje mrežu prizme čija je baza jednakokračni trapez.

Kolekcija zadataka 4

Zadatak 7.

Baza je prizme jednakokračni trapez s osnovicama duljina $26 cm$ i $1 dm$ te krakom duljine $17 cm .$ Visina je te prizme $6.5 cm .$ Izračunajte oplošje i volumen te prizme.

Slika prikazuje dijelove mreže prizme kojoj je baza jednakokračni trapez.

Duljinu visine baze dobivamo s pomoću Pitagorina poučka primijenjena na istaknuti pravokutni trokut. Uvrštavanjem u izraz $v^{2} = b^{2} - {(\frac{c - a}{2})}^{2}$ dobivamo $v^{2} = 17^{2} - 8^{2} = 289 - 64 = 225,$ tj. $V = 15 cm .$

Površina je baze jednaka $B = \frac{a + c}{2} \cdot v = \frac{10 + 26}{2} \cdot 15 = 18 \cdot 15 = 270 {cm}^{2},$ površina je pobočja $P = a h + c h + 2 b h = (a + 2 b + c) \cdot h = 70 \cdot 6.5 = 455 {cm}^{2},$ a oplošje je $O = 2 B + P = 2 \cdot 270 + 455 = 995 {cm}^{2} .$

Volumen je te prizme $V = B h = 270 \cdot 6.5 = 1 755 {cm}^{3} .$

Zadatak 8.

Baza je prizme jednakokračni trapez opsega $108 cm,$ s krakovima duljine $29 cm$ i kraćom osnovicom duljine $0.5 dm .$ Površina je najveće pobočke $13.5 {dm}^{2} .$ Koji su podatci točno određeni?

Duljina je veće osnovice

4.5 dm .

Duljina je visine prizme

3 cm .

Duljina je visine baze

21 cm .

Površina je baze

52.5 {cm}^{2} .

Oplošje je te prizme

429 {cm}^{2} .

Volumen je te prizme

15.75 {dm}^{3} .

null

Zadatak 9.

Povežite prizmu s njezinim odgovarajućim nazivom (imenujte prizmu).

Prizma kojoj je baza osmerokut.	Četverostrana prizma
Prizma s pet pobočki.	Dvanaesterostrana prizma
Prizma kojoj je baza trapez.	Osmerostrana prizma
Prizma sa $14$ strana.	Peterostrana prizma

null

Zatvori

...i na kraju

U ovoj ste jedinici naučili:

imenovati prizme
primijeniti izraze za oplošje i obujam (volumen) uspravne prizme
riješiti problemski zadatak koristeći se mjerljivim obilježjima uspravne prizme.

Primijenite naučeno i izračunajte koliko kubnih metara drva Sanja može spremiti u svoju drvarnicu. Potrebne su mjere označene na slici.

Baza je Sanjine drvarnice pravokutni trapez s osnovicama duljina $2.5 m$ i $3 m,$ a visina je tog trapeza $3 m .$

Uvrštavajući te podatke u izraz za površinu trapeza, dobit ćemo redom $B = \frac{a + c}{2} \cdot v = \frac{2.5 + 3}{2} \cdot 3 = \frac{5.5}{2} \cdot 3 = 2.75 \cdot 3 = 8.25 m^{2} .$

Visina je te prizme $3 m$ pa je njezin volumen jednak $V = B h = 8.25 \cdot 3 = 24.75 m^{3} .$

U Sanjinu drvarnicu stane $24.75 m^{3}$ drva.