Učitelj je učenicima zadao da broj 60 napišu kao umnožak što većeg broja faktora različitih od 1. Andrej, Dorotea i Maša broj su 60 napisali kao umnožak triju faktora. Evo kako je to učinio svatko od njih.
| Andrej | 60=2·2·15 |
| Dorotea | 60=4·3·5 |
| Maša | 60=2·6·5 |
Nakon toga javio se Luka koji tvrdi da je pronašao način da broj
60 prikaže kao umnožak četiriju faktora.
| Luka | 60=2·2·3·5 |
A zatim se javio Petar koji je tvrdio da se broj može zapisati kao umnožak beskonačno mnogo faktora.
| Petar | 60=2·2·3·5·1·1·1... |
Tko je od njih bio najuspješniji u rješavanju zadanog zadatka?
Najuspješniji je bio Luka koji je broj
60 rastavio na
4 faktora. Petar nije pazio na uvjet zadatka prema kojem svi faktori moraju biti različiti od jedan, zato njegovo rješenje nije valjano.
Primjer 1.
Napiši broj 120 kao umnožak što više faktora različitih od broja 1. Promotri dobivene faktore. Što zamjećuješ?
120=2·60=2·2·30=2·2·2·15=2·2·2·3·5
Najveći broj faktora dobili smo kad smo broj 120 napisali kao umnožak brojeva 2, 2, 2, 3 i 5. Svi ti faktori su prosti brojevi.
Svaki se složeni broj može napisati u obliku umnoška prostih faktora. Rastav na proste faktore broja je jedinstven.
Primjer 2.
Rastavi broj 48 na proste faktore.
Neki od postupaka rastava broja
48 na proste faktore.
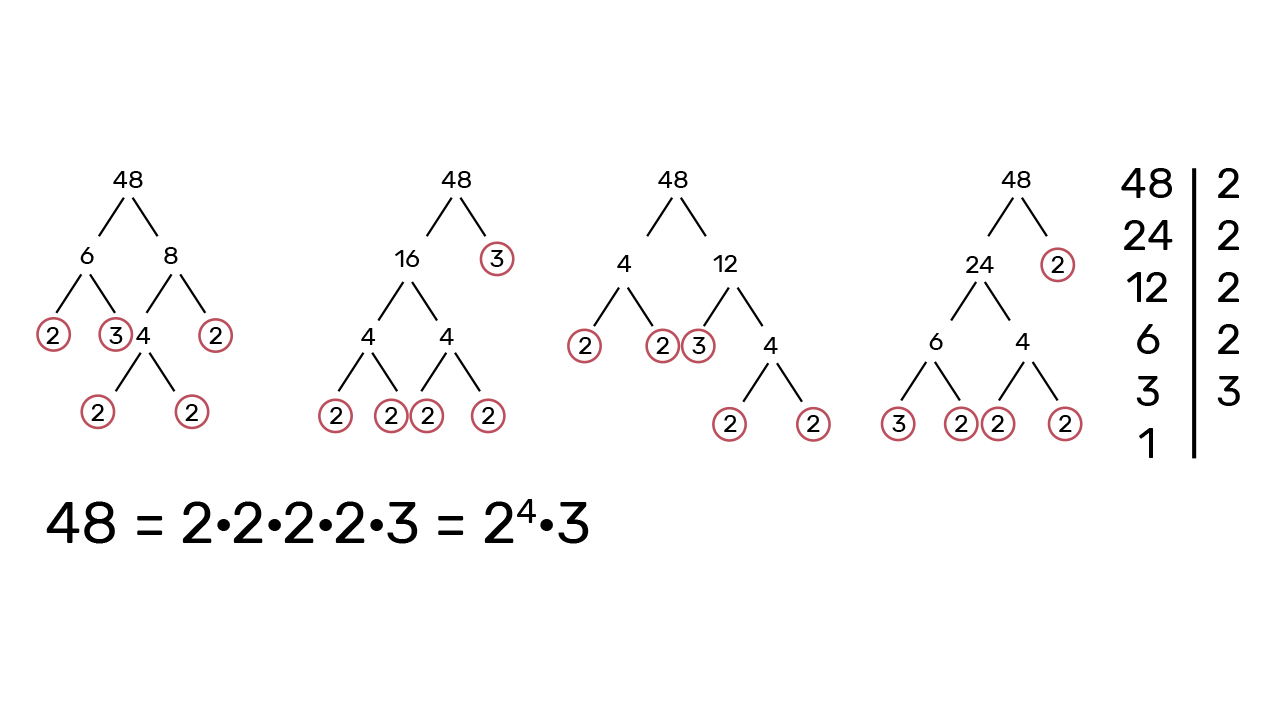
Postupak rastava broja na proste faktore (prvi način):
1. Broj možemo rastaviti na proste faktore tako da ga napišemo kao umnožak neka dva broja (koja prva prepoznamo iz tablice množenja i s pomoću pravila djeljivosti).
2. Svaki od tih brojeva, koji nije prost, nastavljamo pisati kao umnožak neka dva broja.
3. Postupak ponavljamo dok nam ne ostanu samo prosti faktori.
4. Svaki put kad napišemo faktor koji je prost broj, zaokružimo ga.
Postupak rastava broja na proste faktore (drugi način):
1.
Broj redom dijelimo s prostim brojevima dok ne dobijemo količnik
1.
2. Svaki put postupak dijeljenja s prostim brojem ponovimo na količniku (rezultatu) iz prethodnog koraka.
3. Na kraju proste brojeve s kojima smo dijelili zapišemo u obliku umnoška. To je traženi umnožak prostih faktora.
Rastavi zadane brojeve na proste faktore.
a)
18
b)
41
c)
100
d)
117
a) Iz tablice množenja možemo se prisjetiti da je
3 puta
6 jednako
18. Faktor
3 je prost te ga zaokružujemo, a broj
6 rastavljamo na umnožak brojeva
2 i
3. Oba su broja prosta te ih zaokružujemo.
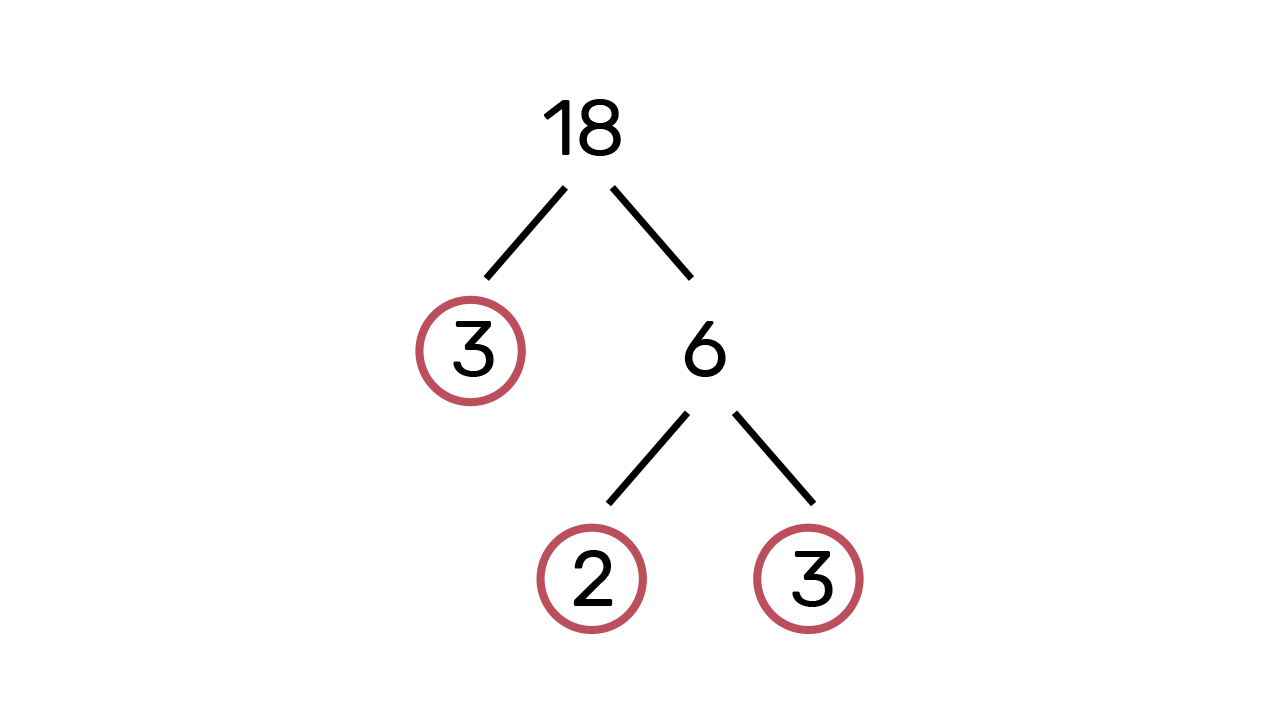
Na kraju prikažemo rastav broja
18 na proste faktore.
18=2·3·3=2·32
b) Broj
41 je prost broj te ga ne moramo rastavljati na proste faktore.
c) Broj
100 završava znamenkom
0 te je djeljiv brojem
10. Broj
100 zapisujemo kao umnožak faktora
10 i
10. Broj 10 je složen broj te ga pišemo kao umnožak faktora
2 i
5. Oba su broja prosta te ih zaokružujemo.
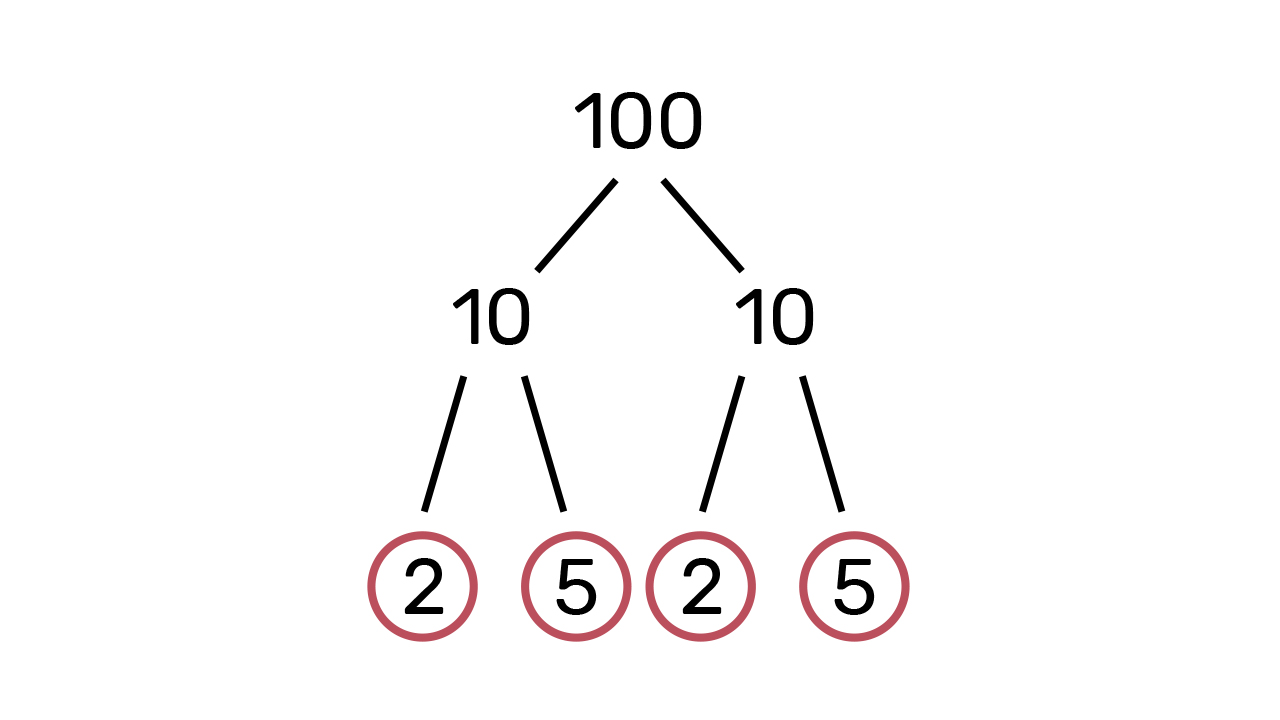
Na kraju prikažemo rastav broja
100 na proste faktore.
100=2·2·5·5=22·52
d) Zbroj znamenaka broja
117 je
9, zato je broj djeljiv brojem
9. Računamo
117:9 i dobivamo
13. Broj
9 je složen broj te ga dalje rastavljamo, a broj
13 zaokružujemo jer je prost broj. Broj
9 prikazujemo kao umnožak broja
3 i broja
3. S obzirom na to da je
3 prost broj, obje trojke zaokružujemo.
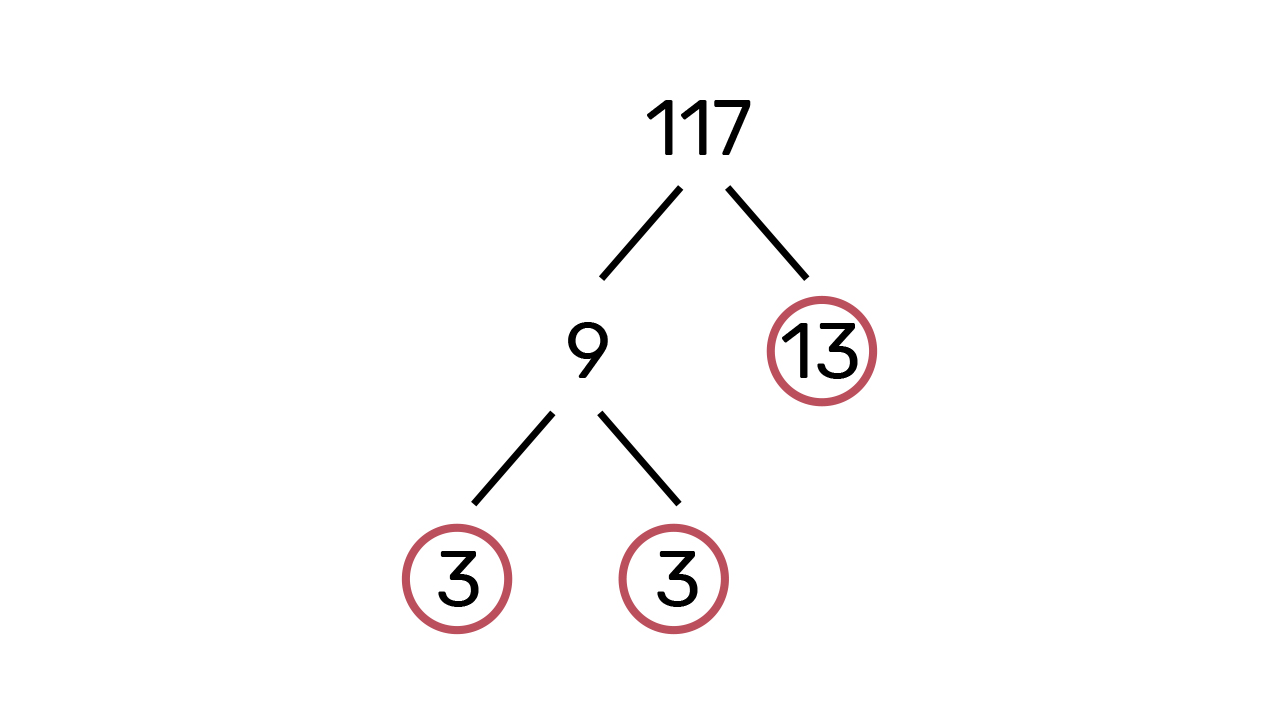
Na kraju prikažemo rastav broja 117 na proste faktore.
117=3·3·13=32·13
Poveži broj i njegov rastav na proste faktore.
|
42
|
2·3·7 |
|
125
|
2·2·2·3·5 |
|
99
|
5·5·5 |
|
75
|
3·5·5 |
|
120
|
3·3·11 |
Za kraj možeš uvježbati rastavljanje broja na proste faktore s pomoću igrice. Broj koji se prikazuje na robotu rastavi na proste faktore. Ako to učiniš točno, osvojit ćeš bod. Ako pogriješiš, robot će osvojiti bod.
