Matematika 5 - 6.1 Zbrajanje decimalnih brojeva

Na početku...

Tia je u knjižari kupila knjigu Lažeš, Melita za $39.98 kn,$ $39.98 kn,$ a u u trgovini pola kilograma banana po cijeni od $6.12 kn$ $6.12 kn$ te jogurt po cijeni od $8.80 kn .$ $8.80 kn .$ Koliko je kuna ukupno potrošila?

Djevojčica u rukama nosi dvije vrećice iz kupovine. — Kupnja

Iznos od $39.98 kn$ $39.98 kn$ možemo prikazati kao iznos od $39$ $39$ kuna i $98$ $98$ lipa. Na isti način je $6.12 kn$ $6.12 kn$ jednako $6 kn$ $6 kn$ i $12 lp$ $12 lp$ te je $8.80 kn$ $8.80 kn$ jednako $8 kn$ $8 kn$ i $80 lp .$ $80 lp .$ Sada zasebno možemo zbrojiti kune, a zasebno lipe.

$39 + 6 + 8 = 53 kn$ $39 + 6 + 8 = 53 kn$

$98 + 12 + 80 = 190 lp$ $98 + 12 + 80 = 190 lp$

Znamo da jedna kuna ima $100$ $100$ lipa te zaključujemo da je $190$ $190$ lipa zapravo $1 kn$ $1 kn$ i $90 lp .$ $90 lp .$

Konačno, zbrojimo iznos od $53 kn$ $53 kn$ te iznos od $1$ $1$ kune i $90$ $90$ lipa.

$53 kn + 1 kn + 90 lp = 54 kn 90 lp = 54.90 kn$ $53 kn + 1 kn + 90 lp = 54 kn 90 lp = 54.90 kn$

U prethodnom primjeru smo, pomoću pretvaranja mjernih jedinica, uspjeli zbrojiti decimalne brojeve. No katkad nam taj postupak nije praktičan te nam treba brži i učinkovitiji način zbrajanja decimalnih brojeva. Upravo taj postupak usvojit ćeš i uvježbati u ovoj jedinici.

Primjer 1.

Zbrojimo $2.56$ $2.56$ i $1.25 .$ $1.25 .$

00:00

Primjer 2.

Zbrojimo $1.6$ $1.6$ i $2.45 .$ $2.45 .$

00:00

Decimalne brojeve zbrajamo na isti način kao i prirodne brojeve. Pri tome moramo paziti na potpisivanje. Cijeli dio potpisuje se pod cijeli dio, decimalna točka pod decimalnu točku, desetinke pod desetinke, stotinke pod stotinke...

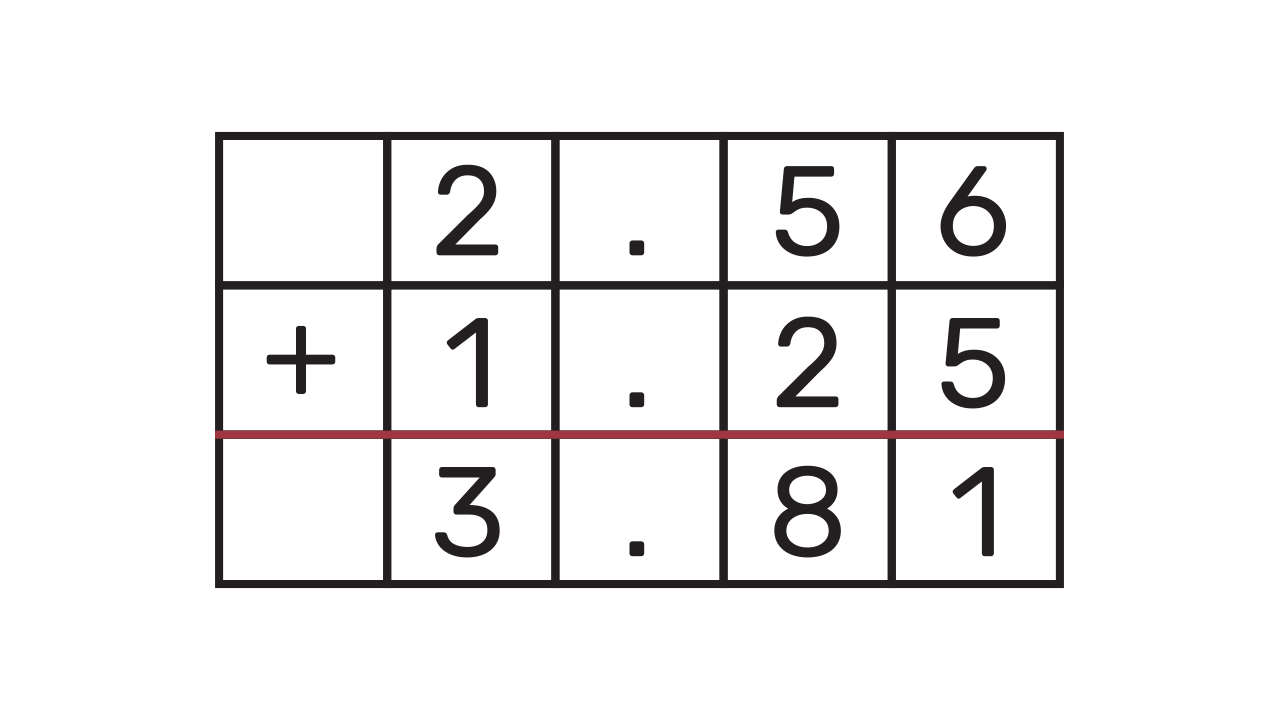
Zbrajanje 2.56 + 1.25=3.81 — Zbrajanje 2.56 + 1.25

Ako decimalni brojevi nemaju jednak broj decimala, iza zadnje decimale dopisujemo potreban broj znamenki $0 .$ $0 .$ (Prisjeti se, $1.6 = 1.60 = 1.600 ...$ $1.6 = 1.60 = 1.600 ...$ )

Prva tablica
1.6
+2.45
=4.05

Druga tablica
1.60
+2.45
=4.05 — Zbrajanje 1.6 + 2.45

Zadatak 1.

Izračunaj.

3.4 + 5.2 =

$3.4 + 5.2 =$

null

7.8 + 2.5 =

$7.8 + 2.5 =$

null

24.53 + 6.39 =

$24.53 + 6.39 =$

null

3.67 + 5.88 =

$3.67 + 5.88 =$

null

Zadatak 2.

Izračunaj.

5.4 + 12.36 =

$5.4 + 12.36 =$

null

3.567 + 1.7 =

$3.567 + 1.7 =$

null

201.5 + 1.78 =

$201.5 + 1.78 =$

null

Primjer 3.

Zoran trenira za Zagrebački maraton. U prvom satu pretrčao je $12.3 km,$ $12.3 km,$ a u drugom $10.8 km .$ $10.8 km .$ Zoran tvrdi da je u ta dva sata ukupno pretrčao $23.1 km. N$ $23.1 km. N$ jegova prijateljica Mihaela tvrdi da je on pretrčao $22.11 km .$ $22.11 km .$ Tko je u pravu?

$\begin{matrix} 12.3 + 10.8 - --- - 23.1 \end{matrix}$ $\begin{array}{r} 12.3 \\ \underline{+ 10.8} \\ 23.1 \end{array}$

Tri desetinke više $8$ $8$ desetinki jednako je $11$ desetinki, tj. jedno cijelo i jedna desetinka. Stoga pišemo $1$ desetinku, a jedno cijelo pribrajamo znamenkama jedinica. Jedno cijelo više $2$ cijela više $0$ cijelih jednako je $3$ cijela. Jedna desetica više $1$ desetica jednako je dvije desetice.

$12.3 + 10.8 = 23.1$

Zoran je u pravu.

Mihaela je zbrojila desetinke te je dobila $11$ desetinki, a zatim je tih jedanaest desetinki netočno zapisala kao $11$ stotinki.

Zadatak 3.

Uvježbaj zbrajanje decimalnih brojeva pomoću sljedećeg apleta.

Zadatak 4.

Poveži zadatak i njegovo rješenje.

$\begin{array}{r} 2.5 \\ \underline{+ 3.7} \end{array}$	$6.2$
$\begin{array}{r} 0.95 \\ \underline{+ 5.27} \end{array}$	$6.3$
$\begin{array}{r} 2.47 \\ \underline{+ 3.83} \end{array}$	$6.22$
$\begin{array}{r} 3.62 \\ \underline{+ 2.5} \end{array}$	$6.12$

null

Zbrajanje decimalnih brojeva s prirodnim brojem

Primjer 4.

Marta želi tapisonom prekriti pod u dječjim sobama. Površina poda prve sobe iznosi $6.3 m^{2},$ a druge $7 m^{2} .$ Koliko kvadratnih metara tapisona treba kupiti?

$6.3 m^{2} + 7 m^{2} = 63 000 {cm}^{2} + 70 000 {cm}^{2} = 133 000 {cm}^{2}$ $= 13.3 m^{2}$

$6.3 + 7 = 13.3$ jer je $6.3 + 7.0 = 13.3$

Prisjeti se, kad iza prirodnog broja dopišemo točku, nakon točke možemo dopisati koliko god nula želimo, a da se vrijednost prirodnog broja ne promijeni.

$7 = 7.0 = 7.00 = 7.000 ...$

Prirodne i decimalne brojeve zbrajamo tako da zbrojimo prirodni broj i cijeli dio decimalnog broja, a decimalni dio samo prepišemo.

Zadatak 5.

Poveži zadatak i njegovo rješenje.

$0.48 + 9 =$	$12.3$
$7 + 5.48 =$	$11.3$
$7.3 + 5 =$	$12.48$
$5 + 6.3 =$	$9.48$

null

Svojstva zbrajanja decimalnih brojeva

Primjer 5.

Ribar Jure prvoga je dana ulovio $15.7 kg$ lignji, a drugoga dana nije ulovio ni jednu lignju. Koliku je masu lignji ulovio u ta dva dana zajedno?

$15.7 + 0 = 15.7$

Ribar Jure u ta dva dana ulovio je ukupno $15.7 kg$ lignji.

Ako decimalnom broju pribrojimo nulu, broj se neće promijeniti.

Za svaki decimalni broj $a$ vrijedi

$a + 0 = 0 + a = a$

Primjer 6.

Prvoga dana Ivan je u pekarnici kupio perec za $3.50 kn,$ a zatim u trgovini jogurt za $8.95 kn .$ Drugoga dana svratio je u trgovinu te kupio jogurt za $8.95 kn,$ a zatim je u pekarnici kupio perec za $3.50 kn .$ Kojeg je dana više potrošio - prvog dana ili drugog dana?

$3.50 + 8.95 = 12.45$

$8.95 + 3.50 = 12.45$

Ivan je oba dana potrošio jednak iznos.

Ako pribrojnici zamijene mjesta, zbroj se neće promijeniti. To se svojstvo naziva komutativnost zbrajanja.

Za svaka dva decimalna broja $a$ i $b$ vrijedi $a + b = b + a .$

Primjer 7.

Petra je trebala stići na posao. Najprije ju je prijateljica Martina vozila $7.4 km$ od kuće do stanice vlaka. Nakon toga Petra je vlakom prešla $21.9 km,$ a zatim je još prehodala $2.6 km .$ Petra i Martina žele izračunati ukupnu udaljenost koju je Petra prešla od kuće do posla.

Petra je zapisala $7.4 + 21.9 + 2.6$ te je počela zbrajati $7.4$ i $21.9 .$ Martina tvrdi da će joj biti jednostavnije odrediti zbroj ako prvo pribroji $7.4$ i $2.6 .$ Je li to točno? Hoće li na oba načina Petra dobiti isto rješenje? Objasni svoj odgovor.

$7.4 + 21.9 + 2.6 = 29.3 + 2.6 = 31.9$

$7.4 + 21.9 + 2.6 = (7.4 + 2.6) + 21.9 = 10 + 21.9 = 31.9$

Petra je od kuće do posla ukupno prešla $31.9 km .$

Petra je na oba načina dobila isto rješenje. U drugom načinu rješavanja prvo je zamijenila redoslijed pribrojnika (primijenila je svojstvo komutativnosti). Nakon toga pribrojnike je združila na drugačiji način, a zbroj se nije promijenio. To se svojstvo naziva svojstvo asocijativnosti zbrajanja.

Ako pribrojnike združimo na različite načine, zbroj se neće promijeniti. To se svojstvo naziva svojstvo asocijativnosti zbrajanja.

Za decimalne brojeve $a$ , $b$ i $c$ vrijedi $a + b + c = (a + b) + c = a + (b + c) .$

Zadatak 6.

Dopuni brojem tako da vrijedi jednakost.

$1.7 + 2.56 = 2.56 +$

null

$10 +$

$= 3.6 + 10 .$

null

Zadatak 7.

Odaberi odgovarajuće svojsto.

$6.3 + 1.6 + 5.4 = 6.3 + (1.6 + 5.4)$
$6.23 + 5.1 = 5.1 + 6.23$

null

Zadatak 8.

Odaberi odgovarajuće svojstvo.

$1.23 + 3.1 + 5.762 = (1.23 + 3.1) + 5.762$
$11 + 0.34 = 0.34 + 11$

null

Zadatak 9.

Izračunaj na najjednostavniji način.

a) $3.75 + 5.2 + 0.25 + 3.8$

b) $5.26 + 4.17 + 1.83 + 2.74$

Promotrimo pribrojnike i združimo one koji daju cjelobrojni međuzbroj.

a) $\begin{array}{l} 3.75 + 5.2 + 0.25 + 3.8 = (3.75 + 0.25) + (5.2 + 3.8) = 4 + 9 = 13 \end{array}$

b) $\begin{array}{l} 5.26 + 4.17 + 1.83 + 2.74 = (5.26 + 2.74) + (4.17 + 1.83) = 8 + 6 = 14 \end{array}$

Primjena zbrajanja decimalnih brojeva

Zadatak 10.

Petra i Magdalena naručuju što žele pojesti i popiti.

	Cijena
Kava	$9.80 kn$
Kava s mlijekom	$10.25 kn$
Sok	$14.99 kn$
Sendvič	$25.63 kn$
Sladoled	$12.34 kn$
Kolač	$22 kn$

Petra je naručila kavu s mlijekom, sendvič i kolač, a Magdalena kavu, sok i sladoled.

a) Koliko je cijena Petrine, a kolika Magdalenine narudžbe?

b) Koliko će obje sve ukupno platiti?

c) Odlučile su iznos računa zaokružiti na najbližu deseticu da bi ostavile napojnicu. Koliko će platiti obje narudžbe zajedno s napojnicom?

a) $10.25 + 25.63 + 22 = 57.88 kn$

Cijena Petrine narudžbe iznosi $57.88 kn .$

$9.80 + 14.99 + 12.34 = 37.13 kn .$

Cijena Magdalenine narudžbe iznosi $37.13 kn .$

b) $57.88 + 37.13 = 95.01 kn$

Ukupno će platiti $95.01 kn .$

c) $95.01 \approx 100$

Svoju će narudžbu zajedno s napojnicom platiti $100 kn .$

Zadatak 11.

Luka je u prodavaonici kupio $2.4 kg$ jabuka, $1.76 kg$ banana, $2 kg$ krumpira, $0.25 kg$ maslaca i lubenicu od $6.789 kg .$ Na putu do kuće vrećice su mu se činile teške te je procjenjivao koliku ukupnu masu u kilogramima nosi u vrećicama. Kod kuće je izračunao točnu masu svih namirnica.

Luka je u prodavaonici kupio približno

$kg$ namirnica.
Ukupna masa namirnica iznosi točno

$kg .$

null

Zadatak 12.

Fabijan je pronašao recept za dječji punč.

$2.5 l$ soka od naranče

$1.85 l$ soka od jabuke

$0.5 l$ voćnog čaja

$0.15 l$ limunovog soka

Pri posluživanju dodati koricu cimeta, klinčić, naranče, jabuke, krišku limuna i žlicu meda.

Koliku će količinu dječjeg punča, izraženu u litrama, napraviti koristeći se ovim receptom?

Fabijan će napraviti

$l$ dječjeg punča.

null

Zadatak 13.

Površina Europe iznosi približno $10.37 milijuna {km}^{2}$ dok površina Azije iznosi približno $44.47 milijuna {km}^{2} .$

Približna površina Euroazije iznosi

${km}^{2} .$

null

Zadatak 14.

Štefica je dobila telefonski račun. Iznos računa je $127.44 kn .$ Na taj iznos mora platiti PDV (porez na dodanu vrijednost) u iznosu od $31.86 kn .$ Koliko Štefica mora platiti svoj telefonski račun?

$127.44 + 31.86 = 159.30 kn$

Štefica svoj telefonski račun mora platiti $159.30 kn .$

Na početku...

Primjer 1.

Primjer 2.

Zadatak 1.

Zadatak 2.

Primjer 3.

Zadatak 3.

Zadatak 4.

Zbrajanje decimalnih brojeva s prirodnim brojem

Primjer 4.

Zadatak 5.

Svojstva zbrajanja decimalnih brojeva

Primjer 5.

Primjer 6.

Primjer 7.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Zadatak 9.

Primjena zbrajanja decimalnih brojeva

Zadatak 10.

Zadatak 11.

Zadatak 12.

Zadatak 13.

Zadatak 14.

...i na kraju