Početna veličina slova
Vidjeli smo kako je tramvaj ušao u jednoj točki kružnog toka, a izašao u drugoj točki, pješaci su prešli cestu ispred kružnog toka pa nisu ni sudjelovali u prometu kružnog toka, a biciklistička staza samo se na jednom mjestu približila kružnom toku.
Pogledajte animaciju u kojoj pravac siječe kružnice različitih polumjera. Promotrite sjecišta pravca i kružnice. Što možete uočiti?
Animaciju pokrenite i zaustavite u različitim položajima kako biste otkrili u koliko se točaka sijeku pravac i kružnica.
Pravac i kružnica sijeku se u dvije točke, jednoj točki ili se ne sijeku ni u jednoj točki.
Pažljivo pogledajte slike i otkrijte u koliko se točaka sijeku pravac i kružnica.
Pogledajte animaciju u kojoj su točka
T i pravac
p povezani različitim dužinama. Animaciju pokrenite i zaustavite u različitim položajima. Promotrite duljine tih dužina. Što možete uočiti?
Vidimo da točku i pravac možemo povezati različitim dužinama koje nemaju jednaku duljinu. Primijetimo i kako je najkraća od tih dužina okomica
na zadani pravac
koja prolazi kroz točku
T.
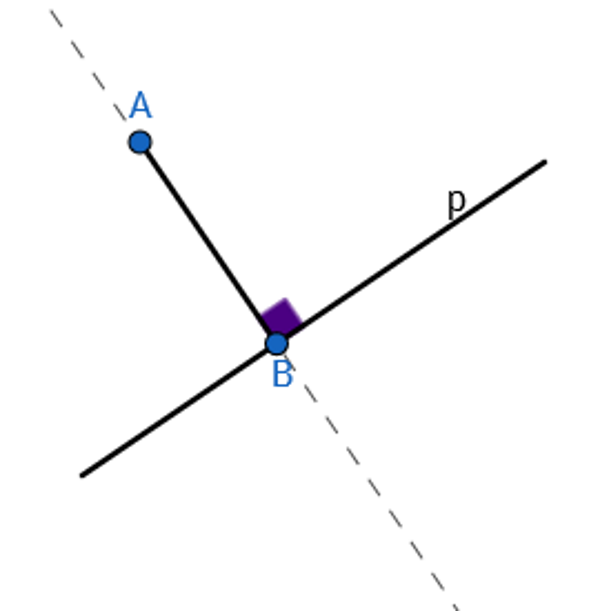
Dani su pravac
p i točka
A. Kroz točku
A povučemo okomicu na pravac
p.
Udaljenost točke A od pravca p je duljina dužine koja spaja točku
A i točku
B u kojoj okomica siječe pravac
p.
d(A,p)=|AB|=d
Nacrtajte na papiru pravac
r
i točku
S
kao na slici. Odredite udaljenost točke
S od pravca
r.
Udaljenost točke
S od pravca
r
moći ćete odrediti ako povučete okomicu iz
točke
S
na pravac
r. Sjecište okomice i pravca
r
označite s
T.
Udaljenost točke S od pravca r je duljina dužine ¯ST.
Konstruirajte na papiru kružnicu polumjera 32mm i pravac koji je od središta udaljen 4cm. U kojem su položaju pravac i kružnica?
Konstruirajte na papiru kružnicu promjera 5cm i pravac koji je od središta kružnice udaljen 25mm. U kojem su položaju pravac i kružnica?
Točka i pravac imaju jednu zajedničku točku.
Konstruirajte na papiru kružnicu promjera 4cm i pravac koji je od središta kružnice udaljen 17mm. U kojem su položaju kružnica i pravac?
Ako je udaljenost središta kružnice i pravca veća od duljine polumjera kružnice, pravac kružnicu točki.
Pomoć:
Pažljivo promotrite prethodne zadatke.
Ako je udaljenost središta kružnice i pravca jednaka duljini polumjera kružnice, pravac kružnicu točki.
Pomoć:
Pažljivo promotrite prethodne zadatke.
Ako je udaljenost središta kružnice i pravca manja od duljine polumjera kružnice, pravac kružnicu
točke.
Pomoć:
Pažljivo promotrite prethodne zadatke.
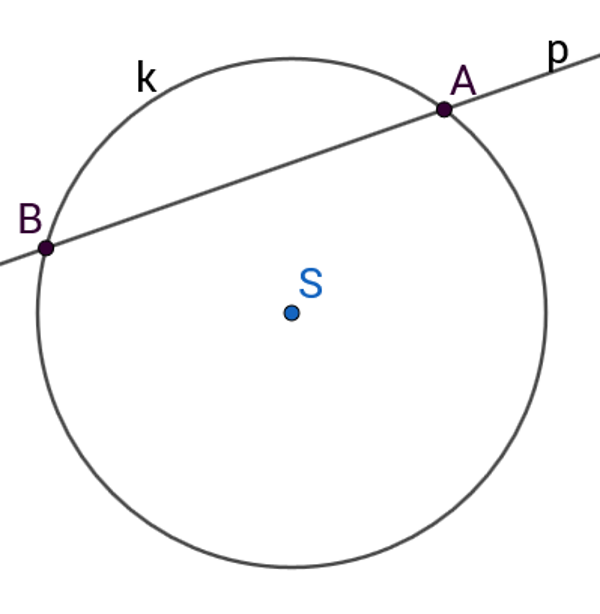
Promotrite sliku. U koliko točaka pravac siječe kružnicu?
Ako pravac siječe kružnicu u dvjema točkama, za njega kažemo da je sekanta kružnice.
Primjer 1.
Zadana je kružnica polumjera 3cm i točke A i B koje leže na kružnici. Odredite sekantu kroz te dvije točke.
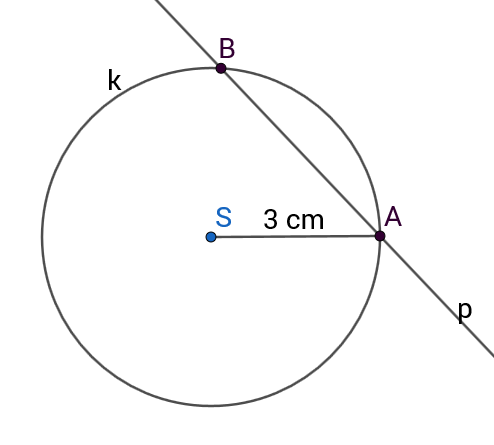
Sekanta kružnice je pravac koji prolazi točkama A i B .
Nacrtajte
na papiru
kružnicu polumjera
4cm i na njoj dvije točke
C i
D. Nacrtajte sekantu kroz te dvije točke.
Konstruirajte na papiru kružnicu k(S,2.5cm) i točke T, R, P na kružnici. Koliko sekanti možete provući kroz zadane točke?
Kroz zadane točke možemo provući tri sekante.
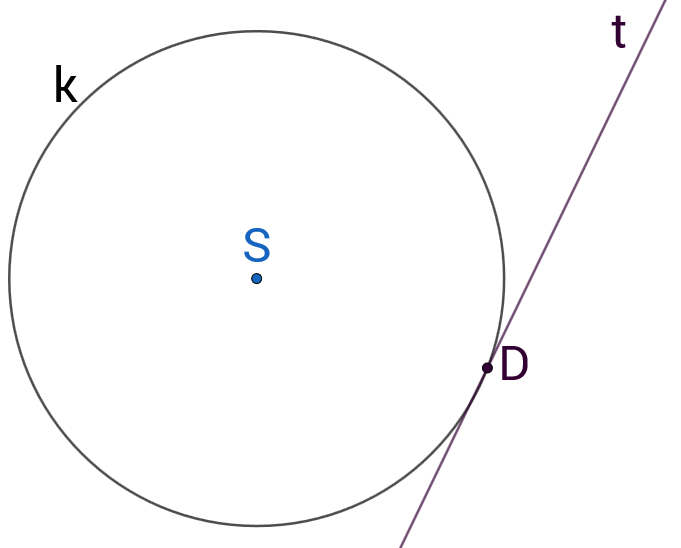
Ako pravac i kružnica imaju jednu točku zajedničku, pravac u toj točki dodiruje kružnicu. Pravac koji dodiruje kružnicu nazivamo tangenta kružnice, a točku u kojoj dodiruje kružnicu nazivamo diralište.
Primjer 2.
Konstruirajmo kružnicu polumjera 2cm i označimo na njoj jednu točku D. Konstruirajmo u točki D tangentu na tu kružnicu.
Pogledajte animaciju u kojoj su prikazani koraci konstrukcije tangente na kružnicu polumjera
2cm u proizvoljnoj točki
D. Klikom na narančaste gumbe pokrećete i zaustavljate animaciju, a klikom na ljubičaste gumbe idete na prethodne ili sljedeće korake.
Uočite u kakvom su odnosu tangenta
t i polumjer
¯SD.
Polumjer koji spaja središte kružnice s diralištem tangente i tangenta međusobno su okomiti.
Pronađite parove.
Odgonetnite nazive pravaca sa slika.
|
|
|
|
|
Pomoć:
Pažljivo pogledajte slike i odgonetnite nazive pravaca.
Konstruirajte
na papiru
kružnicu polumjera
2cm i njezinu sekantu koja je od središta kružnice udaljena
15mm.
Konstruirajte
na papiru
kružnicu polumjera
3.5cm i tangentu kroz točku
T koja leži na kružnici.
Konstruirajte
na papiru
zajedničku tangentu u točki dodira dviju kružnica polumjera
i
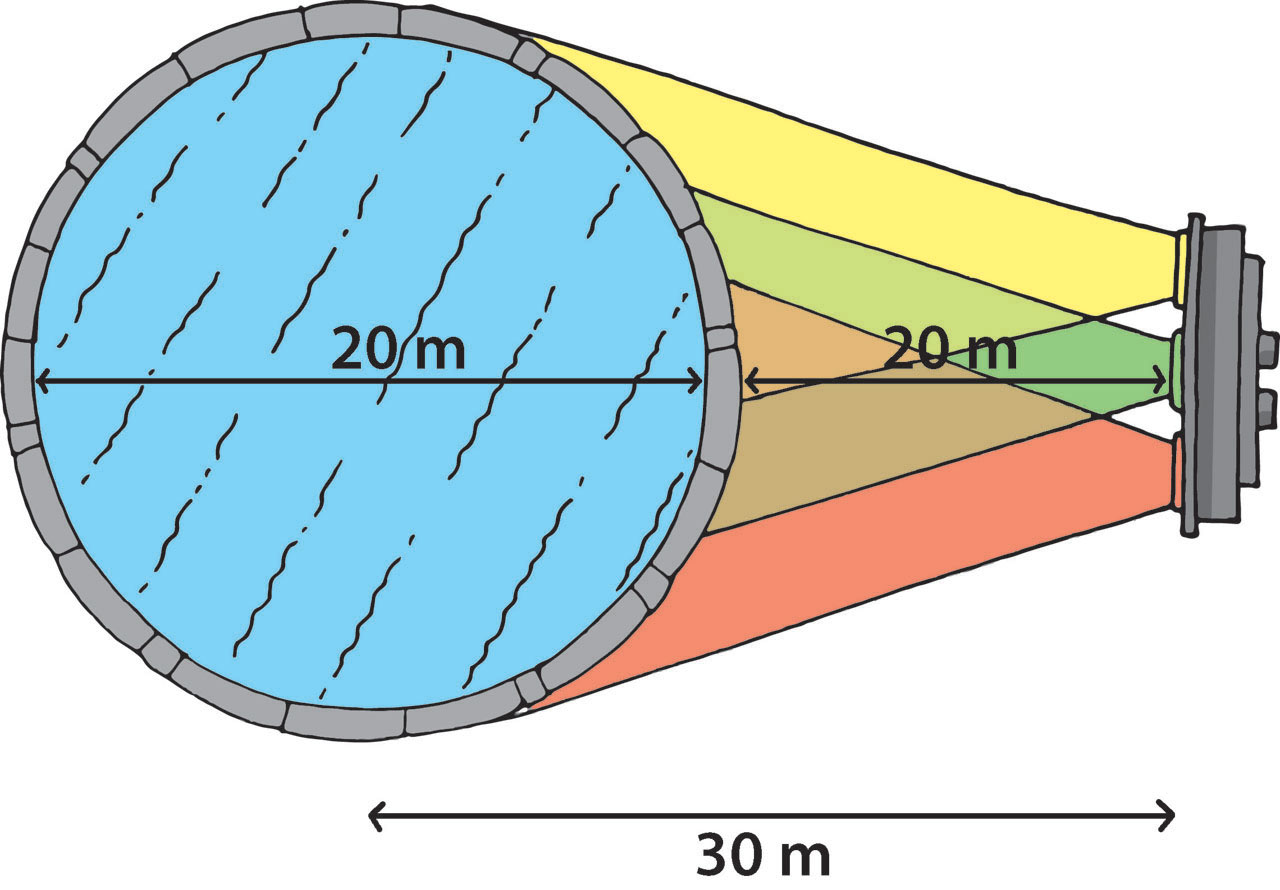
Cvita je dobila zadatak da pomogne u uređivanju gradskih bazena za proslavu Nove godine. Potrebno je postaviti rasvjetu, tako da jedan od reflektora obasjava okrugli bazen promjera metara. Na metara od središta bazena treba staviti reflektor koji će obasjavati samo bazen. Pomozite Cviti u tako važnom zadatku.
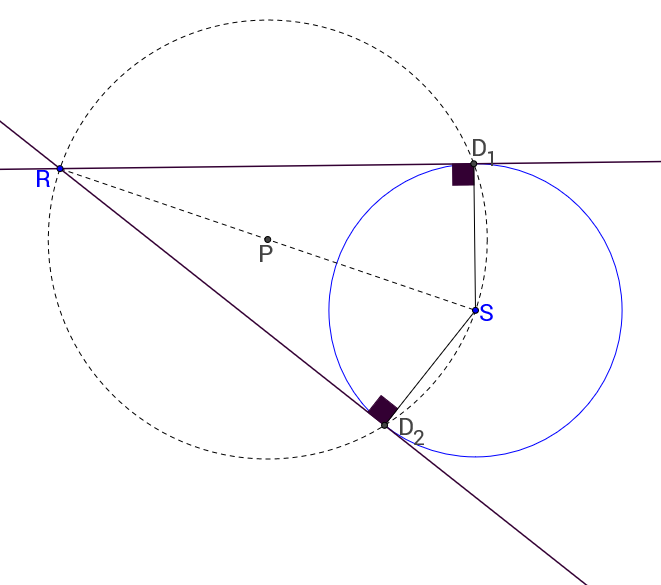
Označimo položaj reflektora točkom
a bazen prikažimo kružnicom sa središtem u točki
promjera
Konstruirajmo dužinu kojoj su krajnje točke
i
Odredimo njezino polovište i označimo ga s
Konstruirajmo kružnicu kojoj je središte u točki
a dužina
njezin polumjer. Njezina sjecišta s kružnicom koja predstavlja bazen označimo s
i
Prema Talesovu poučku znamo da su u točkama i pravi kutovi, pa su pravci i tangente na kružnicu koja predstavlja bazen.
Osmislite zadatak u kojem biste u svojem mjestu postavili novu fontanu i rasvjetu koja će je osvjetljavati, po uzoru na prethodni zadatak. Rezultate svojega rada prikažite plakatima, maketama ili crtežom u nekom od programa dinamičke geometrije, primjerice u GeoGebri ili u Sketchpadu.
Pravac kružnicu dodiruje u jednoj točki, siječe u dvije ili je ne siječe ni u jednoj točki. Ako kružnicu dodiruje u jednoj točki, nazivamo ga tangentom kružnice, a tu točku nazivamo diralištem. Kad pravac siječe kružnicu u dvije točke, nazivamo ga sekantom kružnice.
S pomoću animacije ponovite odnos pravca i kružnice. Animaciju pokrećete klikom na gumb Pokreni, a zaustavljate klikom na gumb Zaustavi. Klikom na potvrdni okvir pokraj naziva pojedinog pravca određeni pravac možete dodati u animaciju ili ga maknuti iz nje.
