Processing math: 100%

2.5 Grafički prikaz proporcionalnih veličina

Što ću naučiti?

Napisati tablicu uređenih parova proporcionalnih veličina
Grafički prikazati proporcionalne veličine u pravokutnom koordinatnom sustavu
Povezati različite prikaze proporcionalnih veličina (tablično, grafički, formulom)
Analizirati grafičke prikaze različitih proporcionalnosti u istom pravokutnim koordinatnom sustavu

Samostalno učenje

Procijenite svoje znanje

Sadržaj jedinice

Na početku...
Različiti prikazi proporcionalnosti
Analiziramo grafičke prikaze
...i na kraju

Sadržaj jedinice

Na početku...
Različiti prikazi proporcionalnosti
Analiziramo grafičke prikaze
...i na kraju

Povećanje slova

Smanjenje slova

Početna veličina slova

Visoki kontrast

a Promjena slova

Upute za korištenje

Na početku...

Točka do točke

Želimo napisati niz točaka, takvih da je druga koordinata dvostruko veća od prve. Dopunite niz brojevima koji nedostaju pa zatim nacrtajte te točke u koordinatnom sustavu.

Iz točaka kod kojih je druga koordinata dvostruko veća od prve:

$A ($

Pogledajte uputu.

$0),$

$B (1,$

Pogledajte uputu.

$),$

$C ($

Pogledajte uputu.

$4),$

$D (3,$

Pogledajte uputu.

$),$

$F (4, 8) .$

Pomoć:

Druga je koordinata dvostruko veća od prve.

null

Povežemo li sve zadane točke ravnom crtom dobit ćemo .

null

Različiti prikazi proporcionalnosti

Interaktivni sadržaj pokazuje količinu jabuka i iznos novca koji za određenu količinu treba platiti. Klizačem zadajemo cijenu za jedan kilogram jabuka. Mijenjajte jediničnu cijenu pa pratite vrijednosti u tablici i grafički prikaz u koordinatnom sustavu.

Kako su povezane vrijednosti u tablici i točke u koordinatnom sustavu?

Uočite kako su točke raspoređene u koordinatnom sustavu. Jesu li nasumično razbacane ili slijede neko pravilo?

Primjer 1.

Cijena $1$ kilograma jabuka iznosi $5 kn .$ Zapišimo u obliku tablice koliko treba platiti za $0, 1, 2, 3, 4 i 5$ kilograma tih jabuka, a zatim dobivene podatke prikažimo grafički.

Količina jabuka koju kupujemo i iznos novca koji za njih trebamo platiti proporcionalne su veličine. Budući da je jedinična cijena za kilogram jabuka $5 kn,$ koeficijent proporcionalnosti iznosi $5$ pa tu proporcionalnost možemo zapisati formulom $y = 5 \cdot x .$

Zapišimo podatke o količini jabuka u tablicu pa izračunajmo redom koliko treba platiti za zadane količine.

To je tablični prikaz proporcionalnosti.

Svaki stupac tablice predstavlja uređeni par količine jabuka i pripadnog iznosa koji za nju treba platiti.

količina $(kg)$	$0$	$1$	$2$	$2$	$3$	$5$
cijena $(kn)$	$0$	$5$	$10$	$15$	$20$	$25$

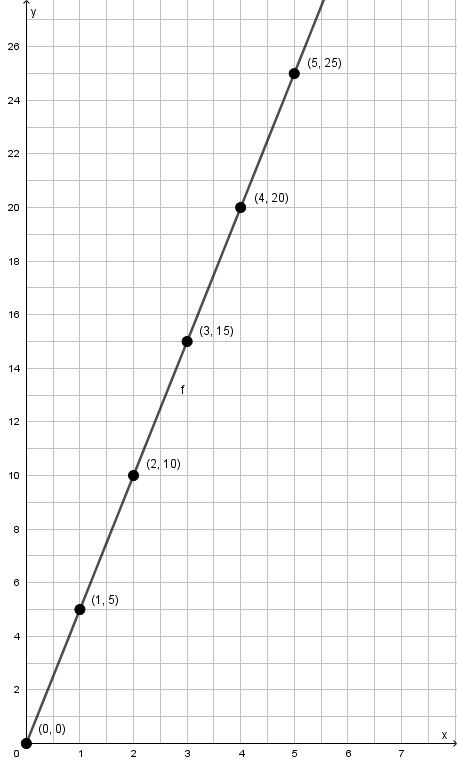
Ucrtajmo te uređene parove $(\begin{array}{l} 0, 0 \end{array}),$ $(\begin{array}{l} 1, 5 \end{array}),$ $(\begin{array}{l} 2, 10 \end{array}),$ $(\begin{array}{l} 3, 15 \end{array}),$ $(\begin{array}{l} 4, 20 \end{array}),$ $(\begin{array}{l} 5, 25 \end{array})$ u pravokutni koordinatni sustav u ravnini. Pri crtanju na $x$ osi stavite razmak $1 cm$ za $1$ komad jabuka, a na $y$ osi možete staviti razmak $1 cm$ za svakih $10$ kuna kako bi vam crtanje bilo lakše.

Na slici vidimo grafički prikaz proporcionalnosti.

Količina jabuka i iznos novca koji za njih trebamo platiti proporcionalne su veličine. U ovom primjeru prikazali smo proporcionalne veličine u obliku formule, tablice te grafičkog prikaza.

Primijetimo da je taj grafički prikaz pravac. S obzirom na to da proporcionalne veličine najčešće gledamo na skupu pozitivnih racionalnih brojeva, možemo reći i da je taj grafički prikaz polupravac s početkom u ishodištu pravokutnog koordinatnog sustava.

Grafički prikaz proporcionalnih veličina jest pravac kroz ishodište. U problemima svakodnevnog života, u kojima se koristimo samo pozitivnim veličinama, grafički prikaz proporcionalnih veličina jest polupravac čija je početna točka u ishodištu.

Zadatak 1.

Koji grafički prikazi pripadaju proporcionalnim veličinama?

Graf proporcionalnosti je pravac kroz ishodište

Graf proporcionalnosti je pravac kroz ishodište

Pomoć:

Graf proporcionalnosti je pravac kroz ishodište

null

Proporcionalnost možemo prikazati formulom, tablicom ili grafički.

Formula $y = 1.2 \cdot x$

Tablica

$x$ $0$ $2$ $4$ $6$

$y$ $0$ $2.4$ $4.8$ $7.2$

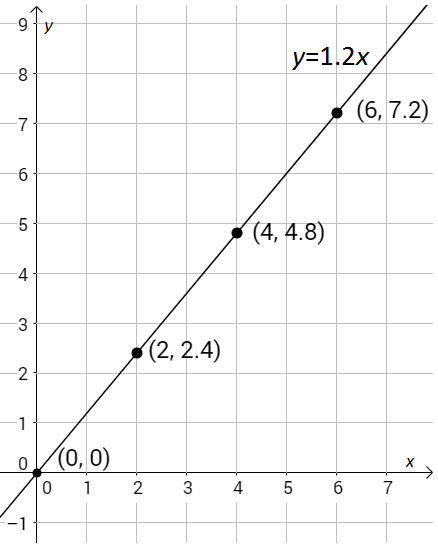
Grafički prikaz proporcionalnosti

Kolekcija zadataka 1

Zadatak 2.

Zadane su proporcionalne veličine formulom i tablicom. Izračunajte vrijednosti koje nedostaju u tablici, a zatim ih što preciznije ucrtajte u koordinatni sustav. Točnost svog rješenja provjerite crtanjem pravca kroz prvu i zadnju točku koju ste ucrtali. Ako ste dobro crtali, sve točke bi se trebale naći na istom pravcu. Ponovite ovaj zadatak nekoliko puta dok ne budete zadovoljni svojom vještinom računanja vrijednosti i crtanja u koordinatnom sustavu.

Zadatak 3.

Odaberite grafički prikaz koji pokazuje podatke dane tabličnim prikazom proporcionalnih veličina.

$x$	$y$
$0$	$0$
$1$	$0.5$
$2$	$1$
$3$	$1.5$
$4$	$2$
$5$	$2.5$
$6$	$3$
$7$	$3.5$

Pažljivo pogledajte tablicu.

null

Zatvori

Kolekcija zadataka 2

Zadatak 4.

Po tečajnoj listi za $1$ euro dobije se $7.5 kn .$ Zapišite u bilježnicu tu proporcionalnost formulom, tablicom te grafički. Za tablicu zadajte vrijednosti eura od $0$ do $5 .$

Iznosi novca u eurima i kunama proporcionalne su veličine s koeficijentom proporcionalnosti

$7.5$ pa zapisujemo formulom

$y = 7.5 \cdot x .$

Tablični prikaz

Iznos u eurima	$0$	$1$	$2$	$3$	$4$	$5$
Iznos u kunama	$0$	$7.5$	$15$	$22.5$	$30$	$37.5$

Grafički prikaz:

Zadatak 5.

Automobil se kreće stalnom brzinom $60 km/h .$ Izračunajte duljinu puta koji prijeđe za $1,$ $2$ i $3$ sata pa dobivene vrijednosti prikažite u bilježnicu grafički. Jesu li vrijeme putovanja i duljina puta u ovom zadataku proporcionalne veličine? Ako jesu, zapišite proporcionalnost formulom.

Prikažimo vrijeme putovanja i duljinu puta tablično.

vrijeme ( $h$ )	$1$	$2$	$3$
duljina puta ( $km$ )	$60$	$120$	$180$

Grafički prikaz porporcionalnih veličina

Grafički prikaz (vrijeme je označeno s $t,$ a duljina puta sa $s$ ).

Da, vrijeme putovanja i duljina puta u ovom su zadataku proporcionalne veličine, što zapisujemo formulom $y = 60 \cdot x .$

Zadatak 6.

Označite koja formula odgovara grafičkom prikazu na slici.

$y = \frac{1}{2} \cdot x$

Bravo!

$y = 2 \cdot x$

Pogladajte uputu

$y = \frac{2}{3} \cdot x$

Pogladajte uputu

$y = 1.5 \cdot x$

Pogladajte uputu

Pomoć:

Točke s grafa zapišiteu bilježnicu u tablicu i iz tablice odredite koeficijent proporcionalnosti.

null

Zatvori

Analiziramo grafičke prikaze

Kolekcija zadataka 4

Zadatak 10.

Na slici su nacrtana dva pravca koji su grafički prikazi ovisnosti količine potrošenog goriva o prijeđenom putu. Pogledajte sliku pa odgovorite na pitanja.

Grafički prikaz ovisnosti količine potrošenog goriva o prijeđenom putu

Koji automobil troši više goriva?
Procijenite razliku u potrošnji na $500 km .$
Koliki su koeficijenti proporcionalnosti?
Kako se najčešće izražava potrošnja goriva nekog automobila, u omjeru prema čemu?
Postavite još neko pitanje na koje se može odgovoriti na temelju zadanih grafičkih prikaza.

Plavi automobil troši više goriva.
Plavi automobil na $500 km$ potroši $45 L$ goriva, a ljubičasti $30 L$ goriva za istu udaljenost. Razlika u potrošnji na $500 km$ iznosi $15 L .$
Koeficijent proporcionalnosti za plavi automobil iznosi $0.09,$ a za ljubičasti $0.06 .$
Najčešće se izražava u obliku količine goriva koju automobil potroši za $100 km .$

Zadatak 11.

Za dva kilograma smokava u Zagrebu treba platiti $38 kn,$ a u Splitu $3$ kilograma treba platiti $45 kn .$

Prikažite u bilježnicu grafički obje proporcionalnosti u istom koordinatnom sustavu.
U kojem je gradu cijena smokava povoljnija?
Koliko treba platiti za $8 kg$ smokava u Splitu?

a. Grafički prikaz:

b. Cijena smokava povoljnija je u Splitu.

c. $8 kg$ smokava u Splitu treba platiti $75 kn .$

Zatvori

...i na kraju

Grafički prikaz proporcionalnosti jest pravac kroz ishodište. U problemima svakodnevnog života grafički prikaz poporcionalnih veličina jest polupravac kojemu je početna točka u ishodištu. Grafički prikaz nam olakšava rješavanje nekih zadataka jer u njemu lakše uočimo razlike između promjena proporcionalnih veličina. Grafički prikaz može nam pomoći i u provjeravanju rješenja koja smo dobili tabličnim prikazom jer svi podaci iz tablice proporcionalnih veličina prikazani u koordinatnom sustavu trebaju biti na istom pravcu.

Zadatak 12.

Samovrednovanje - provjerite znate li riješiti ove zadatke. Najprije ih samostalno riješite, a zatim svoje rješenje usporedite s našim.

Cijena litre benzina iznosi $9.5 kn .$ Nacrtajte u bilježnicu tablicu i izračunajte koliko treba platiti $0,$ $5$ i $10$ litara benzina. Nacrtajte grafički prikaz pa iz njega pročitajte koliko treba platiti $7$ litara benzina.
Kilogram srdelica prodaje se u ribarnici za $20 kn .$ Nacrtajte u bilježnicu tablicu i izračunajte koliko treba platiti $0,$ $2$ i $4 kg$ srdelica. Nacrtajte grafički prikaz pa iz njega pročitajte koliko treba platiti $5 kg$ srdelica.
U trgovini "Iza ugla" $2$ litre vode prodaju za $12 kn,$ a u trgovini "Na kružnom toku" $3$ litre vode prodaju za $15 kn .$ Izračunajte potrebne podatke i obje proprocionalnosti u bilježnici prikažite u istom koordinatnom sustavu. Koja je trgovina povoljnija za kupovinu $6$ litara vode?

a. Sedam litara benzina treba platiti $66.50 kn .$

b. Pet $kg$ srdelica treba platiti $100 kn .$

c. Povoljnije je kupiti $6$ litara u trgovini "Na kružnom toku" jer ćemo je ondje platiti $30 kn,$ a u trgovini "Iza ugla" platili bismo $36 kn .$

Idemo na sljedeću jedinicu

2.5 Grafički prikaz proporcionalnih veličina

Na početku...

Različiti prikazi proporcionalnosti

Zadatak 1.

Kolekcija zadataka 1

Zadatak 2.

Zadatak 3.

Kolekcija zadataka 2

Zadatak 4.

Zadatak 5.

Zadatak 6.

Kolekcija zadataka 3

Zadatak 7.

Zadatak 8.

Zadatak 9.

Analiziramo grafičke prikaze

Kolekcija zadataka 4

Zadatak 10.

Zadatak 11.

...i na kraju

Zadatak 12.

2.6 Obrnuto proporcionalne veličine