4.4 Sljedeća jedinica Soli
4.3

Ravnotežna konstanta ionizacije vode i pH-vrijednost

Moći ću:
  • objasniti ravnotežnu konstantu ionizacije vode, K_{\textrm{w}}
  • izračunati pH i pOH-vrijednosti vodenih otopina
  • odabrati indikatore za kiseline i lužine
  • objasniti važnost pH-vrijednosti vodenih otopina u svakodnevnom životu

Uvod

U reakciji s kiselinama molekule vode su proton akceptori.
U reakciji s bazama molekule vode su proton donori .

Poznata je činjenica da kemijski čista voda slabo provodi električnu struju jer je koncentracija iona u njoj vrlo mala.
Kako nastaju ioni u kemijski čistoj vodi?

Ionski produkt vode

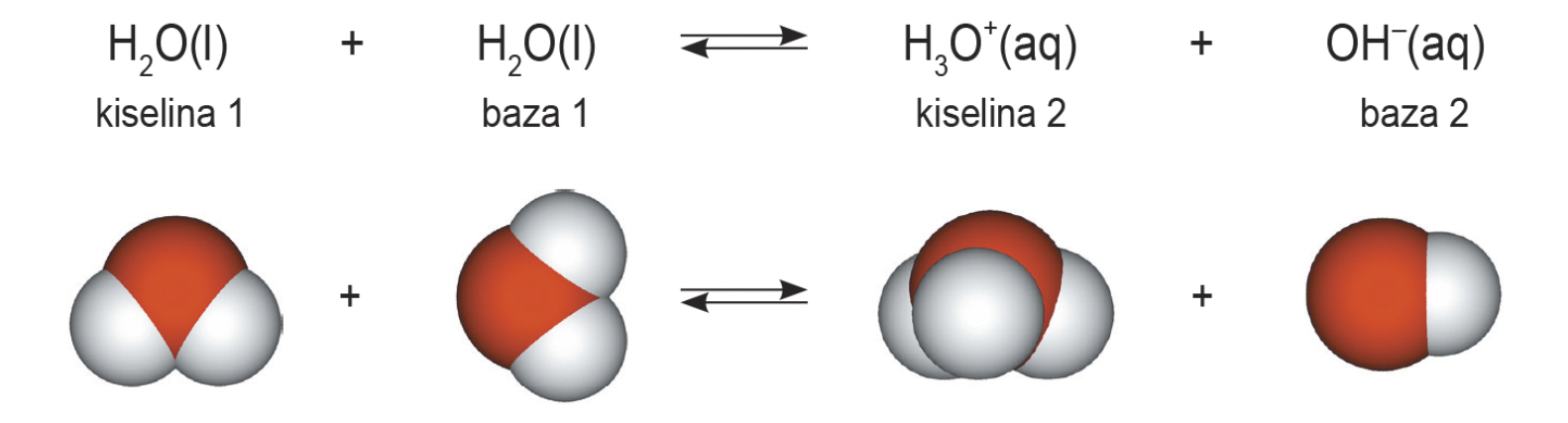
U čistoj se vodi nalazi vrlo mali broj oksonijevih ( \ce{H3O+} ) i hidroksidnih ( \ce{OH-} ) iona koji nastaju pri prijelazu protona s jedne molekule vode na drugu.

Uvod

U reakciji s kiselinama molekule vode su proton akceptori , a u reakciji s bazama proton donori .

Poznata je činjenica da kemijski čista voda slabo provodi električnu struju jer je koncentracija iona u njoj vrlo mala.

Kako nastaju ioni u kemijski čistoj vodi?

Ionski produkt vode

U čistoj se vodi nalazi vrlo mali broj oksonijevih i hidroksidnih iona koji nastaju pri prijelazu protona s jedne molekule vode na drugu.

U gornjoj reakciji ravnoteža je pomaknuta prema molekulama vode.

U ovoj su reakciji molekule vode i proton-donori i proton-akceptori.

U čistoj vodi samo jedna od 107 molekula vode podliježe autoprotolizi.

Budući da u reakciji sudjeluju molekule vode, u izraz za ravnotežnu konstantu ionizacije vode uvrštava se množinski udio za vodu, x (H2O).

Za jako razrijeđene vodene otopine vrijedi:

x (H2O)≈ 1.

Prema tome izraz za ravnotežnu konstantu ionizacije vode (Kc) je:

K = \dfrac{[\ce{H3O+}][\ce{OH-}]}{x^{2}(\ce{H2O})}\qquad

K x^{2}(\ce{H2O}) = [\ce{H3O+}][\ce{OH-}]

Umnožak (∙) ravnotežne konstante ionizacije (Kc) vode i kvadrirane vrijednosti množinskog udjela vode daje novu konstantu, konstantu ionskog produkta vode, Kw.
Indeks w dolazi od engleske riječi za vodu – water.

K_{\textrm{w}} = [\ce{H3O+}][\ce{OH-}] .

Iz navedenoga može se zaključiti da je konstanta ionskoga produkta vode,  K_{\textrm{w}} , određena umnoškom (•) ravnotežnih množinskih koncentracija oksonijevih i hidroksidnih iona.

 

U gornjoj reakciji ravnoteža je pomaknuta prema molekulama vode. U ovoj su reakciji molekule vode i proton-donori i proton-akceptori. Kada su istovrsne molekule u reakciji i proton-donori i proton-akceptori takve reakcije nazivamo autoprotoliza. U čistoj vodi samo jedna od 10^7 molekula vode podliježe autoprotolizi.

Budući da u reakciji sudjeluju molekule vode, u izraz za ravnotežnu konstantu ionizacije vode, uvrštava se množinski udio za vodu, x(H2O).

Za jako razrijeđene vodene otopine vrijedi da je x(H2O)≈ 1. Prema tome izraz za ravnotežnu konstantu ionizacije vode je:

K = \dfrac{[\ce{H3O+}][\ce{OH-}]}{x^{2}(\ce{H2O})}\qquad

K x^{2}(\ce{H2O}) = [\ce{H3O+}][\ce{OH-}]

Umnožak ravnotežne konstante ionizacije vode i kvadrirane vrijednosti množinskog udjela vode daje novu konstantu, konstantu ionskog produkta vode, K_{\textrm{w}} , (indeks w dolazi od engleske riječi za vodu – water).

K_{\textrm{w}} = [\ce{H3O+}][\ce{OH-}]

Iz navedenoga može se zaključiti da je konstanta ionskoga produkta vode, K_{\textrm{w}} , određena umnoškom ravnotežnih množinskih koncentracija oksonijevih i hidroksidnih iona.

Ravnotežna koncentracija oksonijevih iona jednaka je omjeru ravnotežne konstante ionizacije vode i ravnotežne množinske koncentracije hidroksidnih iona:

 

[\ce{H3O+}] = \dfrac{K_{\textrm{w}}}{[\ce{OH-}]}

 

Ravnotežna koncentracija hidroksidnih iona jednaka je omjeru ravnotežne konstante ionizacije vode i ravnotežne množinske koncentracije oksonijevih iona:

 

[\ce{OH-}] = \dfrac{K_{\textrm{w}}}{[\ce{H3O+}]}

 

1 / 2

Vrijednost ravnotežne konstante ionizacije vode je eksperimentalno određena i pri 25 °C iznosi:

K_{\textrm{w}} = \pu{1,00E-14 mol2 dm-6}

Koncentracije oksonijevih (H3O+) i hidroksidnih (OH–) iona u čistoj vodi su jednake (=).

Pri 25 °C iznose \pu{1,00E-7 mol dm-3} .

[\ce{H3O+}] = \dfrac{K_{\textrm{w}}}{[\ce{OH-}]} \qquad [\ce{OH-}] = \dfrac{K_{\textrm{w}}}{[\ce{H3O+}]}

 

Vrijednost ravnotežne konstante ionizacije vode je eksperimentalno određena i pri 25 °C iznosi:

K_{\textrm{w}} = \pu{1,00E-14 mol2 dm-6}

Koncentracije oksonijevih i hidroksidnih iona u čistoj vodi su jednake i pri 25 °C iznose  \pu{1,00E-7 mol dm-3} .

Tablica 1. Vijednosti eksperimentalno određenih ravnotežnih konstanti ionizacije vode pri različitim temperaturama
t / °C K_{\textrm{w}} / \pu{mol2 dm-6}
0 \pu{1,15E-15}
15 \pu{4,56E-15}
25 \pu{1,00E-14}
37 \pu{2,04E-14}
40 \pu{2,83E-14}
60 \pu{8,94E-14}

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Proučite podatke u tablici 1.

Odgovorite na sljedeće pitanje.

Množinska koncentracija (c) oksonijevih iona (H3O+) u vodi pri 40 °C (t) je

puta (•) veća (>) od množinske koncentracije (c) oksonijevih iona (H3O+) pri 15 °C (t).

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte koncentraciju hidroksidnih iona ⦋OH–⦎ u otopini pri 25 °C, ako je koncentracija oksonijevih iona ⦋H3O+⦎ 2,55 × 10–5 mol dm–3 .
Je li otopina kisela ili bazična?

[OH–] =

× 10–10 mol dm–3

Otopina je

zbog toga što je koncentracija
iona
(veća (>) / manja (<) od
iona.

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Proučite podatke u tablici 1. i odgovorite ne sljedeće pitanje.

Množinska koncentracija oksonijevih iona u vodi pri 40 °C je

puta veća od množinske koncentracije oksonijevih iona pri 15 °C.

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte koncentraciju hidroksidnih iona u otopini pri 25 °C, ako je koncentracija oksonijevih iona \pu{2,55E-5 mol dm-3} . Je li otopina kisela ili bazična?

Rješenje:

[\ce{OH-}] =
× 10–10 mol dm–3

Otopina je

zbog toga što je koncentracija
iona
(veća / manja) od koncentracije
iona.

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?
Za znatiželjne

Ravnotežna konstanta ionizacije vode iskazana na drugi način

Ravnotežna konstanta ionizacije (Kw) vode može se izraziti i kao umnožak (•) konstante ionizacije kiseline (Ka) i konstante ionizacije baze (Kb).

K_{\textrm{w}} = K_{\textrm{a}}K_{\textrm{b}}

Pokažimo na primjeru!

Za reakciju:


\ce{NH3(aq) + H2O(l) <=> NH4+(aq) + OH-(aq)}

K_{\textrm{b}} = \dfrac{[\ce{NH4+}][\ce{OH-}]}{[\ce{NH3}]}

[\ce{OH-}] = \dfrac{K_{\textrm{b}}[\ce{NH3}]}{[\ce{NH4+}]}


Amonijev ion (NH4+) je u reakciji konjugirana kiselina.

Reagira s vodom prema reakciji:


\ce{NH4+(aq) + H2O(l) <=> NH3(aq) + H3O+(aq)}

K_{\textrm{a}} = \dfrac{[\ce{NH3}][\ce{H3O+}]}{[\ce{NH4+}]}

[\ce{H3O+}] = \dfrac{K_{\textrm{a}}[\ce{NH4+}]}{[\ce{NH3}]}


Dobivene izraze za ravnotežne koncentracije oksonijevih (H3O+) i hidoksidnih iona (OH–) uvrstimo u izraz za ravnotežnu konstantu ionskoga produkta vode (Kw):

K_{\textrm{w}} = \dfrac{K_{\textrm{a}}[\ce{NH4+}]}{[\ce{NH3}]}\cdot \dfrac{K_{\textrm{b}}[\ce{NH3}]}{[\ce{NH4+}]}

K_{\textrm{w}} = K_{\textrm{a}}K_{\textrm{b}}

 

Za znatiželjne

Ravnotežna konstanta ionizacije vode iskazana na drugi način

Ravnotežna konstanta ionizacije vode može se izraziti i kao umnožak konstante ionizacije kiseline i konstante ionizacije baze.

K_{\textrm{w}} = K_{\textrm{a}}K_{\textrm{b}}

Pokažimo na primjeru!

Za reakciju:


\ce{NH3(aq) + H2O(l) <=> NH4+(aq) + OH-(aq)}

K_{\textrm{b}} = \dfrac{[\ce{NH4+}][\ce{OH-}]}{[\ce{NH3}]}

[\ce{OH-}] = \dfrac{K_{\textrm{b}}[\ce{NH3}]}{[\ce{NH4+}]}


Amonijev ion je u reakciji konjugirana kiselina i reagira s vodom prema reakciji:

\ce{NH4+(aq) + H2O(l) <=> NH3(aq) + H3O+(aq)}

K_{\textrm{a}} = \dfrac{[\ce{NH3}][\ce{H3O+}]}{[\ce{NH4+}]}

[\ce{H3O+}] = \dfrac{K_{\textrm{a}}[\ce{NH4+}]}{[\ce{NH3}]}


Dobivene izraze za ravnotežne koncentracije oksonijevih i hidoksidnih iona uvrstimo u izraz za ravnotežnu konstantu ionskoga produkta vode:

K_{\textrm{w}} = \dfrac{K_{\textrm{a}}[\ce{NH4+}]}{[\ce{NH3}]}\cdot \dfrac{K_{\textrm{b}}[\ce{NH3}]}{[\ce{NH4+}]}

K_{\textrm{w}} = K_{\textrm{a}}K_{\textrm{b}}

Riješite zadatak!

Izračunajte konstantu ionizacije konjugirane kiseline, \ce{NH4+} , u reakciji amonijaka s vodom, ako je K_{\textrm{b}}(\ce{NH3}) = \pu{1,8E-5 mol dm-3} .

Rješenje: Ka(NH4+) = 5,6 × 10–10 mol dm–3

pH – vrijednost kao mjera kiselosti otopina

Danski biokemičar S. P. L. Sørensen [čitaj Sernsen] (1909.) uveo je pojam pH-vrijednosti (čitaj pe-ha).

Pojam pH-vrijednosti uveo je zbog vrlo malih množinskih koncentracija (c) oksonijevih ⦋H3O+⦎ i hidroksidnih iona ⦋OH–⦎,

pH-vrijednost se definira kao negativni logaritam (– log) brojčane vrijednosti množinske koncentracije (c) oksonijevih iona ⦋H3O+⦎.

textrm{pH} = -\log \dfrac{[\ce{H3O+}]}{\pu{mol dm-3}}

Dakle, može se reći da pH vrijednost na kodirani način daje informaciju o množinskoj koncentraciji (c) oksonijevih iona ⦋H3O+⦎ u jako razrijeđenoj vodenoj otopini.

pOH – vrijednost se definira kao negativni logaritam (– log) brojčane vrijednosti množinske koncentracije (c) hidroksidnih iona ⦋OH–⦎.

\textrm{pOH} = -\log \dfrac{[\ce{OH-}]}{\pu{mol dm-3}}

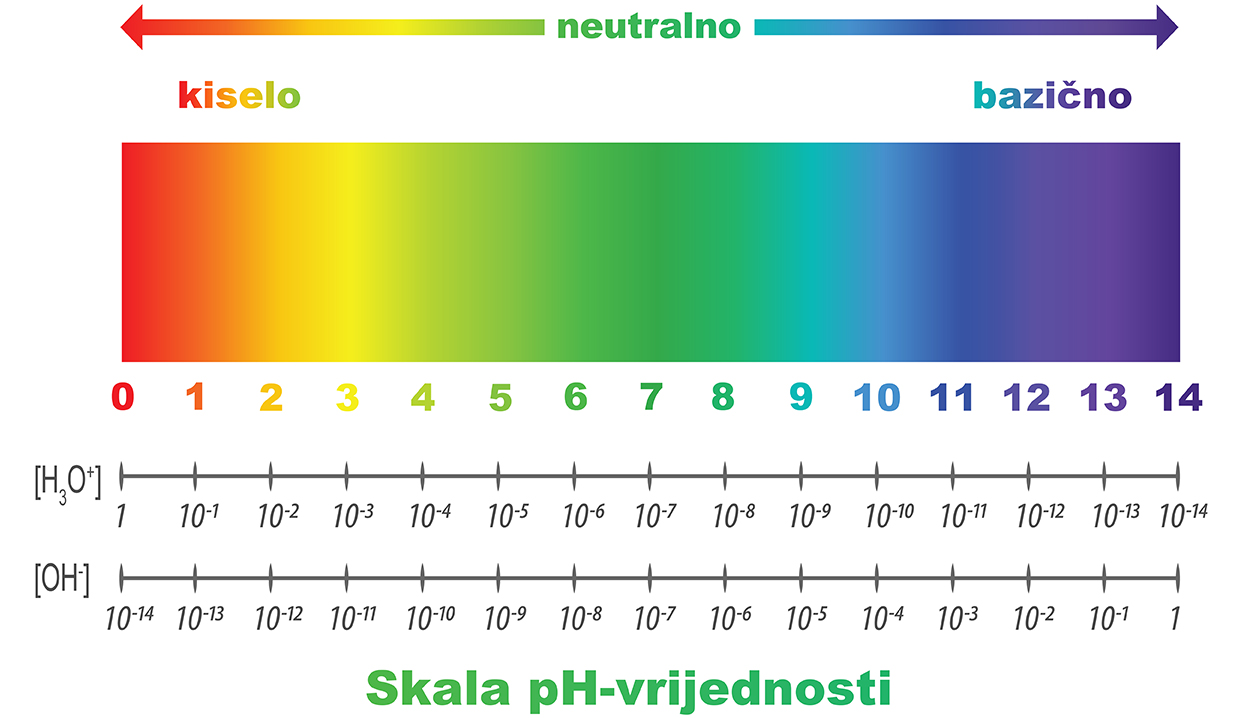
U kiselim otopinama koncentracije oksonijevih iona ⦋H3O+⦎ su veće (>) od 10–7 mol dm–3.

To znači da je pH-vrijednost kiselih otopina manja (<) od 7.

U bazičnim otopinama koncentracije oksonijevih iona ⦋H3O+⦎ su manje (<) od 10–7 mol dm–3.

To znači da je pH-vrijednost bazičnih otopina veća (>) od 7.

Za vodene otopine pri 25 °C vrijedi:
pH + pOH = 14

U destiliranoj vodi pri 25 °C koncentracije oksonijevih ⦋H3O+⦎ i hidroksidnih iona ⦋OH–⦎ su jednake (=).

One iznose 1,0 × 10–7 mol dm–3.

 


[\ce{H3O+}] = \pu{1,0E-7 mol dm-3}\quad \textrm{pH} = 7

[\ce{OH-}] = \pu{1,0E-7 mol dm-3}\quad \textrm{pOH} = 7

K_{\textrm{w}} = [\ce{H3O+}][\ce{OH-}] = \pu{1,0E-7 mol dm-3}\cdot\pu{1,0E-7 mol dm-3} = \pu{1,0E-14 mol2 dm-6}

pH-vrijednost kao mjera kiselosti otopina

Zbog vrlo malih množinskih koncentracija oksonijevih i hidroksidnih iona u vodenim otopinama, danski biokemičar S. P. L. Sørensen [Sernsen] 1909. godine uveo je pojam pH-vrijednosti (čitaj pe-ha).

pH-vrijednost se definira kao negativni logaritam brojčane vrijednosti množinske koncentracije oksonijevih iona.

\textrm{pH} = -\log \dfrac{[\ce{H3O+}]}{\pu{mol dm-3}}

Dakle, može se reći da pH-vrijednost na kodirani način daje informaciju o množinskoj koncentraciji oksonijevih iona u jako razrijeđenoj vodenoj otopini.

pOH-vrijednost se definira kao negativni logaritam brojčane vrijednosti množinske koncentracije hidroksidnih iona.

\textrm{pOH} = -\log \dfrac{[\ce{OH-}]}{\pu{mol dm-3}}

U kiselim su otopinama koncentracije oksonijevih iona veće od 10^{-7} \pu{mol dm-3} , što znači da je pH-vrijednost kiselih otopina manja od 7.

U bazičnim otopinama koncentracije oksonijevih iona su manje od 10^{-7} \pu{mol dm-3} , što znači da je pH-vrijednost bazičnih otopina veća od 7.

Za vodene otopine pri 25 °C vrijedi: \textrm{pH} + \textrm{pOH} = 14

U destiliranoj vodi pri 25 °C koncentracije oksonijevih i hidroksidnih iona su jednake i iznose \pu{1,0E-7 mol dm-3} .


[\ce{H3O+}] = \pu{1,0E-7 mol dm-3}           \quad \textrm{pH} = 7

[\ce{OH-}] = \pu{1,0E-7 mol dm-3}               \quad \textrm{pOH} = 7

K_{\textrm{w}} = [\ce{H3O+}][\ce{OH-}] 

\: \: = \pu{1,0E-7 mol dm-3}\cdot\pu{1,0E-7 mol dm-3} 

\: \: = \pu{1,0E-14 mol2 dm-6}

pH – vrijednost može imati bilo koju vrijednost na ljestvici od 0 do 14.

Neutralne otopine imaju pH 7.

Kisele otopine imaju pH od 0 do 7.

Bazične otopine imaju pH od 7 do 14.

 

  Tablica 2. Odnos množinskih koncentracija: c(\ce{H3O+}) i  c(\ce{OH-})
 kisele otopine neutralne otopine bazične otopine
c(\ce{H3O+}) > c(\ce{OH-}) c(\ce{H3O+}) = c(\ce{OH-}) c(\ce{H3O+}) < c(\ce{OH-})

pH-vrijednost može imati bilo koju vrijednost na ljestvici od 0 do 14. Neutralne otopine imaju pH = 7, kisele otopine od 0 do 7, a bazične otopine od 7 do 14.

  Tablica 2. Odnos množinskih koncentracija: c(\ce{H3O+}) i  c(\ce{OH-})
 kisele otopine neutralne otopine bazične otopine
c(\ce{H3O+}) > c(\ce{OH-}) c(\ce{H3O+}) = c(\ce{OH-}) c(\ce{H3O+}) < c(\ce{OH-})

Fotografija prikazuje skalu pH-vrijednosti i koncentraciju vodikovih iona. Skala podsjeća na spektar boja od nijansi crvene, žute, zelene, plave do ljubičaste. Nijanse spektra pokazuju pH vrijednosti nekih tvari, od kiselina, preko vode do jakih lužina.
Skala pH-vrijednosti i koncentracija vodikovih iona

Za precizno mjerenje pH-vrijednosti otopina koristi se pH-metar.

Za precizno mjerenje pH-vrijednosti otopina koristi se pH-metar.

Fotografija prikazuje ruku koja u prozirnu posudu uranja uređaj žute boje pod nazivom pH-metar. To je instrument koji se koristi za mjerenje pH-vrijednosti najčešće tekućih uzoraka.
pH-metar

Indikatori

Je li otopina kisela, neutralna ili bazična, može se odrediti:

  1. pH-metrom
  2. pomoću indikatora.

Indikatori su najčešće slabe organske kiseline ili baze.
Svojstvo tvari koja može poslužiti kao indikator je da se struktura njezine molekule mijenja ovisno o mediju u kojem se nalazi:

  1. u neutralnom 
  2. u kiselom
  3. u lužnatom mediju
\ce{HIn(aq)} + \ce{H2O(l)} \ce{<=>} \ce{H3O+(aq)} + \ce{In-(aq)}
↓ ↓
kiseli oblik indikatora bazični oblik indikatora


Indikatori koji mijenjaju boju u točno određenom pH-području zovu se kiselo-bazni indikatori.
Mnoge tvari se koriste kao kiselo-bazni indikatori.
Najpoznatiji među njima su:

  •   I.  lakmus
  •  II. univerzalni indikator
  • III. metiloranž
  • IV. fenolftalein.

Mnoge biljke sadrže u staničnim organelima biljne pigmente: klorofil (zeleno), ksantofil (žuto), karotenoid (narančast) i drugi koji mogu biti indikatori kiselosti ili lužnatosti.

Pigmenti antocijanini (crveni, plavi i ljubičasti) daju boju:

  1. plodovima trešnje, crnog i crvenog grožđa
  2. cvjetovima hibiskusa, ljubičice
  3. listovima crvenoga kupusa.

Indikatori

Je li otopina kisela, neutralna ili bazična, može se odrediti osim pH-metrom i pomoću indikatora.

Indikatori su najčešće slabe organske kiseline ili baze. Svojstvo tvari koja može poslužiti kao indikator je da se struktura njezine molekule mijenja ovisno o mediju u kojem se nalazi – u neutralnom, kiselom ili u lužnatom.

\ce{HIn(aq)} + \ce{H2O(l)} \ce{<=>} \ce{H3O+(aq)} + \ce{In-(aq)}
↓ ↓
kiseli oblik indikatora bazični oblik indikatora

Indikatori koji mijenjaju boju u točno određenom pH-području zovu se kiselo-bazni indikatori.

Mnoge tvari se koriste kao kiselo-bazni indikatori, a najpoznatiji među njima su lakmus, univerzalni indikator, metiloranž i fenolftalein.

Mnoge biljke sadrže u staničnim organelima biljne pigmente: klorofil (zeleno), ksantofil (žuto), karotenoid (narančast) i drugi koji mogu biti indikatori kiselosti ili bazičnosti.

Pigmenti antocijanini (crveni, plavi i ljubičasti) daju boju plodovima trešnje, crnog i crvenog grožđa, cvjetovima hibiskusa, ljubičice, te listovima crvenoga kupusa.

Za znatiželjne
Fotografija prikazuje stilizirani šareni cvijet koji se nalazi u velikom mjehuru sapunice. U pozadini se vidi plavo nebo s mnogo bijelih oblaka.

Biljke kao kiselo-bazni indikatori

Mnoge biljke, odnosno biljni pigmenti, u prirodi djeluju kao indikatori kiselosti ili lužnatosti.

Riješite istraživački zadatak dostupan na izvoru 1 i otkrijte koje su to biljke.

Za znatiželjne
Fotografija prikazuje stilizirani šareni cvijet koji se nalazi u velikom mjehuru sapunice. U pozadini se vidi plavo nebo s mnogo bijelih oblaka.

Biljke kao kiselo-bazni indikatori

Mnoge biljke, odnosno biljni pigmenti, u prirodi djeluju kao indikatori kiselosti ili lužnatosti. Riješite istraživački zadatak dostupan na izvoru 1 i otkrijte koje su to biljke.

Upoznajmo najčešće indikatore!

Metiloranž i fenolftalein

Sve boje univerzalnog indikatora

1 / 2

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

S promjenom temperature mijenja se pH-vrijednost čiste vode.

Izračunajte pH-vrijednost čiste vode pri:

t = 10°C,  Kw = \pu{0,29E-14 mol2 dm-6}
t = 25°C ,  Kw = \pu{1,00E-14 mol2 dm-6}
t = 40°C, Kw = \pu{2,92E-14 mol2 dm-6}

pH čiste vode pri 10 °C je


pH čiste vode pri 25 °C je

pH čiste vode pri 40 °C je

 

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Vodena otopina pri 25 °C ima pH = 8.
Koncentracija hidroksidnih iona (OH–) je :

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

U odmjernu tikvicu od 250 mL ulije se 10,0 mL klorovodične kiseline (HCl) množinske koncentracije (c) \pu{0,150 mol dm-3}

Tikvicu se nadopuni vodom do oznake.

Izračunajte pH-vrijednost otopine nastale razrijeđenjem.

Ne zaboravite: Množina (n) otopljene tvari razrjeđivanjem se ne mijenja.

c  (\ce{HCl}) = \pu{0,150 mol/L}

pH = ?

 

 

Rješenje:

pH =

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

S promjenom temperature mijenja se pH-vrijednost čiste vode. Izračunajte pH-vrijednost čiste vode pri:

10°C,      K_{\textrm{w}} = \pu{0,290E-14 mol2 dm-6}
25°C ,      K_{\textrm{w}} = \pu{1,00E-14 mol2 dm-6}
40°C,      K_{\textrm{w}} = \pu{2,92E-14 mol2 dm-6}

pH čiste vode pri 10 °C je
pH čiste vode pri 25 °C je
pH čiste vode pri 40 °C je
Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Vodena otopina pri 25 °C ima pH = 8. Koncentracija hidroksidnih iona je:

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

U odmjernu tikvicu od 250 mL ulije se 10,0 mL klorovodične kiseline množinske koncentracije \pu{0,150 mol dm-3} i nadopuni vodom do oznake. Izračunajte pH-vrijednost otopine nastale razrijeđenjem.

(Ne zaboravite: Množina otopljene tvari razrjeđivanjem se ne mijenja.)

Rješenje:

pH =

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

pH-vrijednosti otopina jakih kiselina i jakih baza

Jake kiseline i jake baze disociraju u vodi gotovo potpuno, pa vrijedi:

c (H3O+) = c (jake kiseline)
c (OH–) = c (jake baze)

Tablica 1. Jake kiseline
fromula naziv
\ce{HClO4} perklorna
\ce{HI} odovodična
\ce{HBr} bromovodična
\ce{HCl} klorovodična
\ce{H2SO4} sumporna
\ce{HNO3} dušična


Tablica 2. Jake baze
fromula naziv
\ce{CsOH} cezij hidroksid
\ce{RbOH} rubidij hidroksid
\ce{KOH} kalij hidroksid
\ce{NaOH} natrij hidroksid
\ce{LiOH} litij hidroksid
\ce{Ba(OH)2} barijev hidroksid
\ce{Sr(OH)2} stroncij hidroksid
\ce{Ca(OH)2} kalcijev hidroksid

pH-vrijednosti otopina jakih kiselina i jakih baza

Jake kiseline i jake baze ioniziraju u vodi gotovo potpuno, pa vrijedi:

c(\ce{H3O+}) = c(\textrm{jake kiseline})

c(\ce{OH-}) = c(\textrm{jake baze})

 

Tablica 3. Neke jake kiseline i jake baze
kiseline baze
ime formula ime formula
perklorna kiselina \ce{HClO4} rubidijev hidroksid \ce{RbOH}
jodovodična kiselina \ce{HI} kalijev hidroksid \ce{KOH}
bromovodična kiselina \ce{HBr} natrijev hidroksid \ce{NaOH}
klorovodična kiselina \ce{HCl} barijev hidroksid \ce{Ba(OH)2}
sumporna kiselina \ce{H2SO4} stroncijev hidroksid \ce{Sr(OH)2}
dušična kiselina \ce{HNO3} kalcijev hidroksid \ce{Ca(OH)2}


 

 

Riješeni primjer 1

Izračunajte pH-vrijednost otopine dušične kiseline (\ce{HNO3}) .

Množinska koncentracija (c) dušične kiseline (\ce{HNO3}) iznosi 1,50×10−5 mol dm−3.

 

 

Zadano je:

c (HNO3) = 1,50×10−5 mol dm−3

Traži se:

pH = ?

Postupak:

Ionizacija dušične kiseline (\ce{HNO3})

\ce{HNO3(aq) + H2O(l) -> H3O+(aq) + NO3-(aq)}

Budući da je dušična kiselina (\ce{HNO3})
jaka kiselina, potpuno ionizira u vodi.

Iz toga proizlazi da je množinska koncentracija (c) oksonijevih iona (\ce{H3O+})
(H3O+) jednaka (=) množinskoj koncentraciji (c) dušične kiseline (\ce{HNO3}) .


c(\ce{H3O+}) = c(\ce{HNO3}) = \pu{1,50E-5 mol dm-3}

\textrm{pH} = -\log \dfrac{[\ce{H3O+}]}{\pu{mol dm-3}}

\textrm{pH} = -\log \dfrac{\pu{1,50E-5 mol dm-3}}{\pu{mol dm-3}}

pH = 4,82

Odgovor:

pH – vrijednost otopine dušične kiseline (\ce{HNO3}) je 4,82.

Riješeni primjer 1.

Izračunajte pH-vrijednost otopine dušične kiseline množinske koncentracije \pu{1,50E-5 mol dm-3} .

Zadano je:

c(\ce{HNO3}) = \pu{1,50E-5 mol dm-3}

 

Traži se:

pH = ?

Postupak:

Ionizacija dušične kiseline:

 

\ce{HNO3(aq) + H2O(l) -> H3O+(aq) + NO3-(aq)}

 

Budući da je dušična kiselina jaka kiselina, potpuno ionizira u vodi iz čega proizlazi da je množinska koncentracija oksonijevih iona jednaka množinskoj koncentraciji dušične kiseline.


c(\ce{H3O+}) = c(\ce{HNO3}) = \pu{1,50E-5 mol dm-3}

\textrm{pH} = -\log \dfrac{[\ce{H3O+}]}{\pu{mol dm-3}}

\textrm{pH} = -\log \dfrac{\pu{1,50E-5 mol dm-3}}{\pu{mol dm-3}}

pH = 4,82

Odgovor:
pH-vrijednost otopine dušične kiseline je 4,82.

Riješeni primjer 2

Izračunajte pH-vrijednost otopine kalijeve lužine (KOH) množinske koncentracije (c) \pu{0,256 mol dm-3} .

Zadano je:

c (\ce{KOH}) = \pu{0,256 mol dm-3}

Traži se:

pH = ?

Postupak:

Disocijacija kalijeve hidroksida (KOH):

\ce{KOH(s) ->[H2O] K+(aq) + OH-(aq)}

Budući da je kalijeva lužina (KOH) jaka lužina, potpuno disocira u vodi.
Množinska koncentracija (c) hidroksidnih iona ( \ce{OH-} ) jednaka (=) je množinskoj koncentraciji (c) kalijeve lužine ( \ce{KOH} ).


c(\ce{OH-}) = c(\ce{KOH}) = \pu{0,256 mol dm-3}

\textrm{pOH} = -\log \dfrac{[\ce{OH-}]}{\pu{mol dm-3}}

\textrm{pOH} = -\log \dfrac{\pu{0,256 mol dm-3}}{\pu{mol dm-3}}

pOH = 0,592

\textrm{pH} = \pu{14,00} – \pu{0,592}

pH = 13,4

Odgovor:

pH – vrijednost kalijeve lužine ( \ce{KOH} ) je 13,4.

Riješeni primjer 2.

Izračunajte pH-vrijednost otopine kalijeve lužine množinske koncentracije \pu{0,256 mol dm-3} .

Zadano je:
 
c(\ce{KOH}) = \pu{0,256 mol dm-3}
 
Traži se:
 
pH = ?

Postupak:

Disocijacija kalijeva hidroksida:

\ce{KOH(s) ->[H2O] K+(aq) + OH-(aq)}

Budući da je kalijeva lužina jaka lužina, potpuno disocirana u vodi, množinska koncentracija hidroksidnih iona jednaka je množinskoj koncentraciji kalijeve lužine.


c(\ce{OH-}) = c(\ce{KOH}) = \pu{0,256 mol dm-3}

\textrm{pOH} = -\log \dfrac{[\ce{OH-}]}{\pu{mol dm-3}}

\textrm{pOH} = -\log \dfrac{\pu{0,256 mol dm-3}}{\pu{mol dm-3}}

pOH = 0,592

\textrm{pH} = \pu{14,0} – \pu{0,592}

pH = 13,4

Odgovor:
pH-vrijednost kalijeve lužine je 13,4.

Riješeni primjer 3

Izračunajte pH – vrijednost otopine barijeve lužine (Ba(OH)2).

Množinska koncentracija (c) barijeve lužine (Ba(OH)2) iznosi 0,256 mol dm−3.

Zadano je:

c (\ce{Ba(OH)2}) = \pu{0,256 mol dm-3}

Traži se:

pH = ?

Postupak:
Disocijacija barijeva hidroksida  ( \ce{Ba(OH)2} ):

\ce{Ba(OH)2(s) ->[H2O] Ba^{2+}(aq) + 2OH-(aq)}

Iz reakcije disocijacije barijeve lužine (Ba(OH)2) vidljivo je da je koncentracija (c) hidroksidnih iona (OH–) dva puta (2∙) veća (>) od koncentracije (c) lužine.

c (OH–) = 2 ∙ c (\ce{Ba(OH)2})

c  (\ce{OH-}) 2c(\ce{Ba(OH)2}) = 2\cdot\pu{0,256 mol dm-3} = \pu{0,512 mol dm-3}

pOH  = -\log \dfrac{[\ce{OH-}]}{\pu{mol dm-3}}

pOH   = -\log \dfrac{\pu{0,512 mol dm-3}}{\pu{mol dm-3}}

pOH   = 0,291

pOH   = \pu{14,0} – \pu{0,291}

pOH   = 13,7

 

pH – vrijednost barijeve lužine (Ba(OH)2) je 13,7.

Riješeni primjer 3

Izračunajte pH-vrijednost otopine barijeve lužine množinske koncentracije \pu{0,256 mol dm-3} .

Zadano je:

c(\ce{Ba(OH)2}) = \pu{0,256 mol dm-3}

Traži se:

pH = ?

Postupak:

Disocijacija barijeva hidroksida:

\ce{Ba(OH)2(s) ->[H2O] Ba^{2+}(aq) + 2OH-(aq)}

Iz reakcije disocijacije barijeve lužine vidljivo je da je koncentracija hidroksidnih iona dva puta veća od koncentracije lužine.


c(\ce{OH-}) = 2c(\ce{Ba(OH)2}) = 2\cdot\pu{0,256 mol dm-3} = \pu{0,512 mol dm-3}

\textrm{pOH} = -\log \dfrac{[\ce{OH-}]}{\pu{mol dm-3}}

\textrm{pOH} = -\log \dfrac{\pu{0,512 mol dm-3}}{\pu{mol dm-3}}

pOH = 0,291

\textrm{pH} = \pu{14,0} – \pu{0,291}

pH = 13,7

Odgovor:

pH-vrijednost barijeve lužine je 13,7.

pH-vrijednosti otopina slabih kiselina i slabih baza

Za slabe kiseline i slabe baze karakteristično je da slabo disociraju u vodi.
Iz toga slijedi da koncentracija (c) oksonijevih iona (H3O+) slabih kiselina nije jednaka (≠) koncentraciji (c) slabih kiselina.
Odnosno, koncentracija (c) hidroksidnih iona (OH–) nije jednaka (≠) koncentraciji (c) slabih baza.
Da bi se izračunala koncentracija (c) oksonijevih iona (H3O+) potreban je podatak za konstantu ionizacije kiseline, Ka, ili stupanj ionizacije, α, slabe kiseline.
\ce{HA + H2O <=> H3O+ + A-}

K_{\textrm{a}} = \dfrac{[\ce{H3O+}][\ce{A-}]}{[\ce{HA}]}

[\ce{H3O+}] = [\ce{A-}] = x

K_{\textrm{a}} = \dfrac{x^{2}}{[\ce{HA}]}

x= \sqrt{K_{\textrm{a}}[\ce{HA}]}

Tada je :

[\ce{H3O+}]= \sqrt{K_{a}[\ce{HA}]} ili c(\ce{H3O+}) = \alpha \cdot c(\ce{HA})

Stupanj ionizacije (α) slabih kiselina je omjer množinske koncentracije (c) oksonijevih iona (\ce{H3O+}) nastalih ionizacijom slabe kiseline i množinske koncentracije (c) kiseline.

\alpha (\ce{HA}) = \dfrac{[\ce{H3O+}]}{[\ce{HA}]}

 

Na isti način poznavajući konstantu ionizacije baze (Kb) ili stupanj disocijacije (α) slabe baze može se izračunati koncentracija (c) hidroksidnih iona (OH–).

 

\ce{BOH <=> B+ + OH-}

K_{\textrm{b}} = \dfrac{[\ce{B+}][\ce{OH-}]}{[\ce{BOH}]}

[\ce{OH-}] = [\ce{B+}] = x

K_{\textrm{b}} = \dfrac{x^{2}}{[\ce{BOH}]}

x= \sqrt{K_{\textrm{b}}[\ce{BOH}]}

 

Stupanj ionizacije (α) slabih baza je omjer množinske koncentracije (c) hidroksidnih iona (OH–) nastalih ionizacijom slabe baze i množinske koncentracije (c) slabe baze.

 

\alpha (\ce{BOH}) = \dfrac{[\ce{OH-}]}{[\ce{BOH}]}

 

Tablica 1. Slabe kiseline
Formula Naziv
\ce{H2SO3} sumporasta
\ce{H3PO4} fosforna
\ce{CH3COOH} etanska (octena
\ce{H2CO3} ugljična
\ce{H2S} sumporovodična
\ce{HCOOH} metanska (mravlja)
\ce{HNO2} dušikasta
\ce{HOCl} hipoklorasta
\ce{HCN} cijanovodična
\ce{C6H5OH} fenol

 

Tablica 2. Slabe baze
Formula Naziv
\ce{Mg(OH)2} magnezijeva lužina
\ce{NH3(aq)} amonijak
\ce{CH3NH2} metil amin
\ce{CH3CH2NH2} etil amin
\ce{C6H5NH2} anilin

 

Za jedinke koje se ponašaju kao kiseline i kao baze, kažemo da su amfoterne.

Primjerice, hidrogenkarbonatni ioni, HCO3−, u reakciji mogu biti i proton-donori i proton-akceptori.


\ce{HCO3^{-}(aq) + H3O^{+}(aq) -> H2CO3(aq) + H2O(l)}

\ce{HCO3^{-}(aq) + OH^{-}(aq) -> CO3^{2-}(aq) + H2O(l) }

pH-vrijednosti otopina slabih kiselina i slabih baza

Za slabe kiseline i slabe baze karakteristično je da slabo ioniziraju u vodi. Iz toga slijedi da koncentracija oksonijevih iona slabih kiselina nije jednaka koncentraciji slabih kiselina, odnosno koncentracija hidroksidnih iona nije jednaka koncentraciji slabih baza.

Da bi se izračunala koncentracija oksonijevih iona potreban je podatak za konstantu ionizacije kiseline, K_{\textrm{a}} , ili stupanj ionizacije, \alpha , slabe kiseline.

\ce{HA + H2O <=> H3O+ + A-}

K_{\textrm{a}} = \dfrac{[\ce{H3O+}][\ce{A-}]}{[\ce{HA}]}

[\ce{H3O+}] = [\ce{A-}] = x

K_{\textrm{a}} = \dfrac{x^{2}}{[\ce{HA}]}

x = \sqrt{K_{\textrm{a}}[\ce{HA}]}

Tada je:

[\ce{H3O+}]= \sqrt{K_{\textrm{a}}[\ce{HA}]}

Stupanj ionizacije slabih kiselina je omjer množinske koncentracije oksonijevih iona nastalih ionizacijom slabe kiseline i množinske koncentracije kiseline.

\alpha (\ce{HA}) = \dfrac{[\ce{H3O+}]}{[\ce{HA}]}

Na isti način poznavajući konstantu ionizacije baze K_{\textrm{b}} ili stupanj ionizacije slabe baze, \alpha ,  može se izračunati koncentracija hidroksidnih iona.

\ce{BOH <=> B+ + OH-}

K_{\textrm{b}} = \dfrac{[\ce{B+}][\ce{OH-}]}{[\ce{BOH}]}

[\ce{OH-}] = [\ce{B+}] = x

K_{\textrm{b}} = \dfrac{x^{2}}{[\ce{BOH}]}

x= \sqrt{K_{\textrm{b}}[\ce{BOH}]}

Tada je :

[\ce{OH-}]= \sqrt{K_{\textrm{b}}[\ce{BOH}]}

Stupanj ionizacije slabih baza je omjer množinske koncentracije hidroksidnih iona nastalih ionizacijom slabe baze i množinske koncentracije slabe baze.

\alpha (\ce{BOH}) = \dfrac{[\ce{OH-}]}{[\ce{BOH}]}

Slabe kiseline:

\ce{H2SO3} , sumporasta kiselina ; \ce{H3PO4} , fosforna kiselina; \ce{CH3COOH} , etanska (octena) kiselina;
\ce{H2CO3} , ugljična kiselina, \ce{H2S} ; sumporovodična kiselina, \ce{HCOOH} ; metanska (mravlja) kiselina; \ce{HNO2} , dušikasta kiselina; \ce{HOCl} , hipoklorasta kiselina; \ce{HCN} , cijanovodična kiselina; \ce{C6H5OH} , fenol.

Slabe baze:

\ce{Mg(OH)2} , magnezijeva lužina; \ce{NH3(aq)} , amonijak; \ce{CH3NH2} ,
metilamin; \ce{CH3CH2NH2} , etilamin; \ce{C6H5NH2} , anilin.

Za jedinke koje se ponašaju kao kiseline i kao baze, kažemo da su amfoterne.

Primjerice, hidrogenkarbonatni ioni, \ce{HCO3^{-}} , u reakciji mogu biti i proton-donori i proton-akceptori.


\ce{HCO3^{-}(aq) + H3O^{+}(aq) -> H2CO3(aq) + H2O(l)}

\ce{HCO3^{-}(aq) + OH^{-}(aq) -> CO3^{2-}(aq) + H2O(l) }

Riješeni primjer 4.

Izračunajte pH-vrijednost octene kiseline ( \ce{CH3COOH} ).
Množinska koncentracija (c) octene kiseline ( \ce{CH3COOH} ) iznosi 0,200 mol dm-3.
Konstanta ionizacije, Ka, octene kiseline (CH3COOH) iznosi 1,80 × 10–5  mol dm-3.

Zadano je:


c(\ce{CH3COOH}) = \pu{0,200 mol dm-3}

K_a = \pu{1,80E-5 mol dm-3}


Traži se:

pH = ?

Postupak:

Ionizacija octene kiseline  ( \ce{CH3COOH} ) prikazana je jednadžbom:

 

\ce{CH3COOH(aq) + H2O(l) <=> H3O+(aq) + CH3COO-(aq)}

 

Budući da octena kiselina (CH3COOH) ne ionizira u cijelosti, potrebno je uzeti u obzir konstantu ravnoteže, K_{\textrm{a}} .

K_{\textrm{a}} = \dfrac{[\ce{H3O+}][\ce{CH3COO-}]}{[\ce{CH3COOH}]}

Sljedeća tablica u kojoj analiziramo promjenu koncentracije, pomoći će u postavljanju jednadžbe kojom ćemo izračunati koncentraciju oksonijevih iona (H3O+) potrebnu za konačan izračun pH-vrijednosti.

 

 

\ce{CH3COOH(aq)} \ce{H3O+(aq)} \ce{CH3COO-(aq)}
početna
koncentracija / \pu{mol dm-3} 		\pu{0,200} 0 0
promjena -x +x +x
ravnotežna
koncentracija / \pu{mol dm-3} 		\pu{0,200}-x x x

Tražena jednadžba proizlazi iz definicije konstante ravnoteže.


\pu{1,80E-5 mol dm-3} = \dfrac{x^2}{\pu{0,200 mol dm-3} – x}

x^2 = \pu{1,80E-5 mol dm-3}\cdot (\pu{0,200 mol dm-3} – x)

x^2 = \pu{0,200 mol dm-3}\cdot\pu{1,80E-5 mol dm-3} – \pu{1,80E-5 mol dm-3}\cdot x


x^{2} + \pu{1,80E-5 mol dm-3}\cdot x \: – \pu{0,36E-5 mol2 dm-6} = 0

Kvadratna jednadžba:


x^{2} + \pu{1,80E-5}\cdot x \: – \pu{0,36E-5} = 0

ima dva rješenja:

x_1 = \pu{1,89E-3 mol dm-3}

x_2 = -\pu{1,91E-3 mol dm-3}

Kemijski, od dva matematički realna rješenja, samo pozitivna (+) vrijednost množinske koncentracije (c) oksonijevih iona (H3O+) ima smisla:

x = [\ce{H3O+}] = \pu{1,89E-3 mol dm-3}

\textrm{pH} = -\log \dfrac{c(\ce{H3O+})}{\pu{mol dm-3}}

\textrm{pH} = -\log \pu{1,89E-3}

\pu{pH = 2,72}

pH-vrijednost navedene otopine je 2,72.

Međutim, jednadžba koju smo upravo riješili, može se pojednostaviti ako se zbog vrlo slabe ionizacije kiseline zanemari smanjenje početne koncentracije kiseline.
Tada umjesto ravnotežne koncentracije (\pu{0,200 mol dm-3} – x) računamo s početnom koncentracijom \pu{0,200 mol dm-3} .

Tada rješavanje jednadžbe konstante ravnoteže izgleda ovako:


\pu{1,80E-5 mol dm-3} = \dfrac{x^2}{\pu{0,200 mol dm-3}}

x^2 = \pu{1,80E-5 mol dm-3}\cdot \pu{0,200 mol dm-3}

x = \sqrt{\pu{3,60E-6 mol2 dm-6}}

x = [\ce{H3O+}] = \pu{1,89E-3 mol dm-3}

Na kraju treba izračunati pH-vrijednost:

\textrm{pH} = -\log \dfrac{c(\ce{H3O+})}{\pu{mol dm-3}}

\textrm{pH} = -\log \pu{1,89E-3}

\pu{pH = 2,72}

Odgovor: pH-vrijednost navedene otopine je 2,72.

Riješeni primjer 4.

Izračunajte pH-vrijednost octene kiseline, množinske koncentracije \pu{0,200 mol dm-3} , ako je konstanta ionizacije octene kiseline K_{\textrm{a}} = \pu{1,80E-5 mol dm-3} .

Zadano je:

c(\ce{CH3COOH}) = \pu{0,200 mol dm-3}
 
K_{\textrm{a}} = \pu{1,80E-5 mol dm-3}

Traži se:

pH-vrijednost = ?

Izradak:

Ionizacija octene kiseline prikazana je jednadžbom:

\ce{CH3COOH(aq) + H2O(l) <=> H3O+(aq) + CH3COO-(aq)}

Budući da octena kiselina ne ionizira u cijelosti, potrebno je uzeti u obzir konstantu ravnoteže, K_{\textrm{a}} .

K_{\textrm{a}} = \dfrac{[\ce{H3O+}][\ce{CH3COO-}]}{[\ce{CH3COOH}]}

Sljedeća tablica u kojoj analiziramo promjenu koncentracije, pomoći će u postavljanju jednadžbe kojom ćemo izračunati koncentraciju oksonijevih iona, potrebnu za konačan izračun pH-vrijednosti.

Tablica 3. Tablični podatci
  \ce{CH3COOH(aq)} \ce{H3O+(aq)} \ce{CH3COO-(aq)}
početna koncentracija / \pu{mol dm-3} \pu{0,200} 0 0
promjena -x +x +x
ravnotežna koncentracija / \pu{mol dm-3} \pu{0,200}-x x x

Tražena jednadžba proizlazi iz definicije konstante ravnoteže.


\pu{1,80E-5 mol dm-3} = \dfrac{x^2}{\pu{0,200 mol dm-3} – x}

x^2 = \pu{1,80E-5 mol dm-3}\cdot (\pu{0,200 mol dm-3} – x)

x^2 = \pu{0,200 mol dm-3}\cdot\pu{1,80E-5 mol dm-3} – \pu{1,80E-5 mol dm-3}\cdot x


x^{2} + \pu{1,80E-5 mol dm-3}\cdot x \: – \pu{0,36E-5 mol2 dm-6} = 0

 

Kvadratna jednadžba:


x^{2} + \pu{1,80E-5}\cdot x \: – \pu{0,36E-5} = 0

 

ima dva rješenja:

 

x_1 = \pu{1,89E-3 mol dm-3}

 

x_2 = -\pu{1,91E-3 mol dm-3}

 

Kemijski, od dva matematički realna rješenja, samo pozitivna vrijednost množinske koncentracije oksonijevih iona ima smisla:

x = [\ce{H3O+}] = \pu{1,89E-3 mol dm-3}

 

\textrm{pH} = -\log \dfrac{c(\ce{H3O+})}{\pu{mol dm-3}}

\textrm{pH} = -\log \pu{1,89E-3}

\pu{pH = 2,72}

pH-vrijednost navedene otopine je 2,72.

Međutim, jednadžba koju smo upravo riješili, može se pojednostaviti, ako se zbog vrlo slabe ionizacije kiseline zanemari smanjenje početne koncentracije kiseline. Tada umjesto ravnotežne koncentracije (\pu{0,200 mol dm-3} – x) računamo s početnom koncentracijom \pu{0,200 mol dm-3} .

Tada rješavanje jednadžbe konstante ravnoteže izgleda ovako:


\pu{1,80E-5 mol dm-3} = \dfrac{x^2}{\pu{0,200 mol dm-3}}

x^2 = \pu{1,80E-5 mol dm-3}\cdot \pu{0,200 mol dm-3}

x = \sqrt{\pu{3,60E-6 mol2 dm-6}}

x = [\ce{H3O+}] = \pu{1,89E-3 mol dm-3}

 

Na kraju treba izračunati pH-vrijednost:

\textrm{pH} = -\log \dfrac{c(\ce{H3O+})}{\pu{mol dm-3}}

\textrm{pH} = -\log \pu{1,89E-3}

\pu{pH = 2,72}

 

Odgovor: pH-vrijednost navedene otopine je 2,72.

Na kraju…

Rješavanjem interaktivnih zadataka, usustavite pojmove obrađene u ovoj jedinici DOS-a te potom riješite i interaktivni kviz.

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Koji je izraz za konstantu ionizacije (Kw) vode ispravno napisan:

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte volumen (V) klorovodične kiseline (HCl) čiji pH iznosi 5.

Navedenu kiselinu se može pripremiti razrijeđenjem 250 mL klorovodične kiseline (HCl) čiji pH iznosi 2.

pH (HCl) = 5

pH (HCl) = 2

V (HCl) = ?

V (HCl) =

L

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Koliko litara (V) destilirane vode (H2O)  treba dodati u 1 litru vodene otopine dušične kiseline (HNO3) za pripremu otopine dušične kiseline (HNO3).
pH otopine dušične kiseline iznosi 2.

pH (HNO3)= 1

pH otopine HNO3 = 2

V (H2O) = ?

V (H2O) =

L

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

U 500 mL (V) vodene otopine otopljeno je 1,00 g (m) litijeva hidroksida (LiOH).

Koliki je pH vodene otopine?

m (LiOH) = 1,00 g

V (otopine) = 500 mL

pH = ?

pH =

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Ako se u otopinu kapne nekoliko kapi metiloranža otopina se oboji crveno.

Točna tvrdnja je:

 

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Koji je izraz za konstantu ionizacije vode ispravno napisan:

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte volumen klorovodične kiseline pH = 5, koju se može pripremiti razrijeđenjem 250 mL klorovodične kiseline pH = 2.

Rješenje:

V(HCl) =
L
Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Koliko litara destilirane vode treba dodati u 1 L litru vodene otopine dušične kiseline kojoj je pH = 1, za pripremu vodene otopine dušične kiseline kojoj je pH = 2?

Rješenje:

V(HCl) =
L
Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Koliko iznosi pH-vrijednost vodene otopine koja u 500 mL sadrži 1,00 g litijeva hidroksida?

Rješenje:

pH-vrijednost =
Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Ako se u otopinu kapne nekoliko kapi metiloranža otopina se oboji crveno. Točna tvrdnja je:

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?