4.5 Sljedeća jedinica Puferi
4.4

Soli

Moći ću:
  • navesti što su soli
  • pojedinoj soli pridružiti odgovarajući naziv
  • prikazati različite načine dobivanja soli jednadžbama kemijskih reakcija
  • izračunati ravnotežnu konstantu otapanja soli
  • na temelju vrijednosti ravnotežne konstante otapanja soli zaključiti je li sol dobro ili slabo topljiva u vodi
  • predvidjeti pH-vrijednost različitih vodenih otopina soli

Soli

Soli su vrlo važni kemijski spojevi.
Čvrste su tvari.
Sastoje većinom od kationa metala i aniona kiselinskog ostatka.
Nemetalni kation je primjerice amonijev ion, NH4+.
Zbog raznovrsne uporabe soli su dobivale i različita trivijalna imena primjerice:
vapnenac, gips, soda bikarbona, modra galica, salmijak i druge.

Uvod

Soli su vrlo važni kemijski spojevi. To su čvrste tvari koje se sastoje većinom od kationa metala i aniona kiselinskog ostatka. Nemetalni kation je primjerice, amonijev ion, \ce{NH4+} .

Zbog raznovrsne uporabe soli su dobivale i različita trivijalna imena primjerice: vapnenac, gips, soda bikarbona, modra galica, salmijak i druge.

Koje se soli kriju iza ovih naziva i gdje se upotrebljavaju ?

Vapnenac, kalcijev karbonat, \ce{CaCO3}

U prirodi se nalazi u dvama kristalnim oblicima kao mineral kalcit i aragonit.
Stalaktiti odnosno stalagmiti su viseći odnosno stojeći kalcitni sustavi i nalaze se u spiljama diljem svijeta. Stalaktiti nastaju taloženjem kalcijeva karbonata prije nego što kap padne, a stalagmiti nakon što padne na tlo.

U Hrvatskoj se nalazi veliki broj spilja i pećina koje su nastale kemijskim promjenama vezanim uz topljivost kalcijeva karbonata u vodi. Više o njima pronađite na izvoru 1.

Vapnenac ima široku primjenu u građevinarstvu.

Gips ili sadra, kalcijev sulfat dihidrat, \ce{CaSO4 \cdot 2H2O}

Pustinjska ruža kristala gipsa nastala djelovanjem vjetra i vlage u pustinji Sahari, u Tunisu. Sastoji se od lisnatih kristala sadre i zrnaca pijeska.

Gips se rabi u medicini za imobilizaciju lomova, a veliku primjenu ima i u građevinarstvu, kiparstvu i arhitekturi.

Soda bikarbona, natrijev hidrogenkarbonat, \ce{NaHCO3}

Bijeli prah, slabo topljiv u vodi. Koristi se u proizvodnji pjenušavih pića, kao i u sredstvima za čišćenje i slično. Soda bikarbona je glavni, rijetko kada jedini sastojak u prašku za pecivo, u kojemu se još nalaze fosfati koji reguliraju kiselost potrebnu za otpuštanje ugljikova dioksida. Ugljikov dioksid omogućava dizanje tijesta, a dodani kukuruzni škrob pomaže da se tijesto zgusne i poveže.

Otopina sode bikarbone se često koristi kao narodni lijek protiv žgaravice i refluksa  ali bez valjane dijagnoze ne treba pribjegavati ovom “lijeku”.

Modra galica, bakrov(II) sulfat pentahidrat, \ce{CuSO4.5H2O}

Najpoznatija je bakrova sol karakteristične plave boje, dobro topljiva u vodi.

Koristi se kao fungicid u vinogradarstvu protiv peronospore vinove loze (gljivična infekcija na vinovoj lozi). Zbog kisele vodene otopine bakrova(II) sulfata dodaje se gašeno vapno, a dobivena smjesa naziva se “Bordoška juha”.

Salmijak, amonijev klorid, \ce{NH4Cl}

Bijela sol, dobro topljiva u vodi. Upotrebljava se u galvanizaciji, kao elektrolit u suhim baterijama, u smjesama za hlađenje, u sredstvima za pranje i drugo.

1 / 6

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Navedenim kemijskim formulama soli upišite odgovarajuće ime.

\ce{NaCl}

\ce{K2SO4}

\ce{Ca(NO3)2}

\ce{(NH4)3PO4}

\ce{FeCl3}

\ce{FeSO4.7H2O}

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Navedenim kemijskim formulama soli upišite odgovarajuće ime.

\ce{NaCl}

\ce{K2SO4}

\ce{Ca(NO3)2}

\ce{(NH4)3PO4}

\ce{FeCl3}

\ce{FeSO4.7H2O}

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Topljivost soli

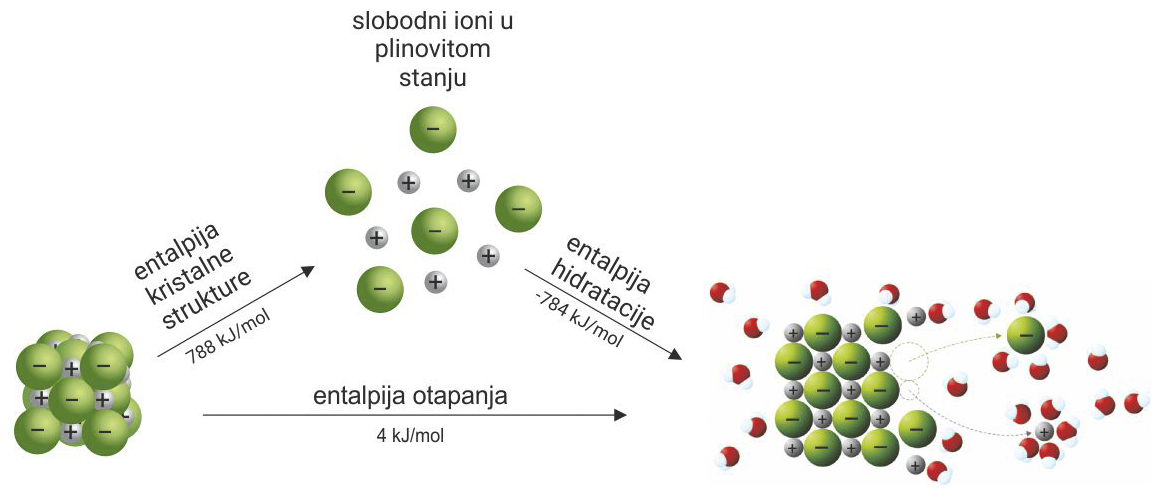
Prilikom otapanja

soli

u vodi razara se ionska kristalna rešetka.
Dolazi do hidratacije nastalih iona, ion – dipolnih interakcija.
Soli su elektrolitne otopine zbog slobodnih iona.

Topljivost soli

Prilikom otapanja soli u vodi razara se ionska kristalna rešetka i dolazi do hidratacije nastalih iona, ion-dipolnih interakcija. Zbog slobodnih iona, vodene otopine soli su elektrolitne otopine.

Otapanje natrijeva klorida prikazano modelom

Jednadžba disocijacije natrijeva klorida (NaCl):
\ce{NaCl(s) ->[H2O] Na+(aq) + Cl-(aq)}

Natrijev kolrid (NaCl)  je dobro topljiva u vodi.
Barijev sulfat (BaSO4) je vrlo slabo topljiv u vodi.
Za soli slabo topljive u vodi uspostavlja se ravnoteža između:

  1. iona na koje sol disocira u vodenoj otopini
  2. netopljive soli.

Jednadžba disocijacije barijeva sulfata (BaSO4):

\ce{BaSO4(s) <=>[H2O] Ba^{2+}(aq) + SO4^{2-}(aq)}

Izraz za koncentracijsku konstantu ravnoteže otapanja barijeva sulfata je:

K_{\textrm{s}} = \dfrac{[\ce{Ba^{2+}}][\ce{SO4^{2-}}]}{[\ce{BaSO4}]}

 

Zbog slabe topljivosti soli pretpostavlja se da je koncentracija barijeva sulfata (BaSO4) konstanta.
Umnožak (∙) koncentracijske konstante ravnoteže (Kc) i množinske koncentracije (c) barijeva sulfata ( \ce{BaSO4} )) daje ravnotežnu konstantu otapanja soli Ks (engl. solubility product constant).

K_{\textrm{s}} = [\ce{Ba^{2+}}][\ce{SO4^{2-}}]

Ravnotežna konstanta otapanja soli, Ks, pri danoj temperaturi, ovisi o umnošku (∙) koncentracije (c) pojedinih iona u otopini, potencirane brojem iona u formuli spoja.

To je razlog zbog kojeg mjerne jedinice ravnotežnih konstanti otapanja  (Ks) navedenih soli, nisu jednake.

Primjerice;


Ks (\ce{CuS}) = [\ce{Cu^{2+}}][\ce{S^{2-}}] = \pu{8E-37 mol2 dm-6}

Ks (\ce{CaF2}) = [\ce{Ca^{2+}}][\ce{F-}]^{2} = \pu{3,45E-11 mol3 dm-9}

Iz ravnotežne konstante otapanja soli (Ks) mogu se izračunati:

  1. koncentracije (c) disociranih iona
  2. topljivost soli pri određenoj temperaturi.

Poveznica za  Tablica topljivosti soli

Što je manja (<) vrijednost ravnotežne konstante otapanja soli (Ks) to je manja njena (<) topljivost.

Jednadžba disocijacije natrijeva klorida:

\ce{NaCl(s) ->[H2O] Na+(aq) + Cl-(aq)}

Za razliku od natrijeva klorida koji je dobro topljiv u vodi, barijev sulfat je vrlo slabo topljiv u vodi.

Za soli slabo topljive u vodi uspostavlja se ravnoteža između iona na koje sol disocira u vodenoj otopini i netopljive soli.

Jednadžba disocijacije barijeva sulfata:

\ce{BaSO4(s) <=>[H2O] Ba^{2+}(aq) + SO4^{2-}(aq)}


Izraz za koncentracijsku konstantu ravoteže otapanja barijeva sulfata je:

K_{\textrm{c}} = \dfrac{[\ce{Ba^{2+}}][\ce{SO4^{2-}}]}{[\ce{BaSO4}]}

Zbog slabe topljivosti barijeva sulfata pretpostavlja se da je njegova koncentracija konstantna.

Umnožak koncentracijske konstante ravnoteže i množinske koncentracije barijeva sulfata, daje ravnotežnu konstantu otapanja soli, K_{\textrm{s}} (engl. solubility product constant) .

K_{\textrm{s}} = [\ce{Ba^{2+}}][\ce{SO4^{2-}}]

Ravnotežna konstanta otapanja soli,  K_{\textrm{s}} , pri danoj temperaturi ovisi o umnošku koncentracije pojedinih iona u otopini potencirane brojem iona u formuli spoja. To je razlog zbog kojih mjerne jedinice ravnotežnih konstanti otapanja navedenih soli, nisu jednake.

Primjerice;


K_{\textrm{s}}(\ce{CuS}) = [\ce{Cu^{2+}}][\ce{S^{2-}}] = \pu{8E-37 mol2 dm-6}

K_{\textrm{s}}(\ce{CaF2}) = [\ce{Ca^{2+}}][\ce{F-}]^{2} = \pu{3,45E-11 mol3 dm-9}


Iz ravnotežne konstante otapanja soli,  K_{\textrm{s}} , mogu se izračunati koncentracije disociranih iona i topljivost soli pri određenoj temperaturi.

Poveznica za Tablicu topljivosti soli.

Što je manja vrijednost ravnotežne konstante otapanja soli,  K_{\textrm{s}} , to je  njena topljivost manja.

Riješeni primjer 1

 

Koja je sol topljivija u vodi, barijev sulfat  (BaSO4) ili barijev fluorid (BaF2)?

Ravnotežna konstanta otapanja (Ks) barijeva sulfata (\ce{BaSO4})  je 1,08×10−10mol2dm−6 pri 25 °C.

Ravnotežna konstanta otapanja (Ks) barijeva fluorida K_{\textrm{s}}(\ce{BaF2}) je 1,84×10−7mol3dm−9 pri 25 °C.

Zadano je:


Ks (\ce{BaSO4}) = \pu{1,08E-10 mol2 dm-6}

Ks (\ce{BaF2}) = \pu{1,84E-7 mol3 dm-9}

Traži se:

c1 (\ce{Ba2+, aq}) = ?

c1 – koncentracija barijevih iona u otopini barijeva sulfata \ce{BaSO4}

c2 (\ce{Ba2+, aq}) = ?

c2 – koncentracija barijevih iona u otopini barijeva flourida  \ce{BaF2}

Izradak:

Iz vrijednosti ravnotežne konstante otapanja može se izračunati koncentracija (c1 i c2) barijevih iona (Ba2+) u vodenoj otopini jedne i druge soli.

Korak 1

Jednadžba disocijacije barijeva sulfata (BaSO4) u vodi.
Ravnotežne koncentracije barijevih (Ba2+) i sulfatnih iona (SO42–) označe se sa x.

\ce{BaSO4(s) <=>[H2O] Ba^{2+}(aq) + SO4^{2-}(aq)}

 

Korak 2

Iz izraza za ravnotežnu konstantu otapanja soli može se izračunati množinska koncentracija (c) barijevih iona (Ba2+):


Ks (\ce{BaSO4}) = [\ce{Ba^{2+}}] [\ce{SO4^{2-}}]

Ks [\ce{BaSO4}] = x\cdot x

Ks [\ce{BaSO4}] = x^2

x = [\ce{Ba^{2+}}] = \sqrt{K_{\textrm{s}}[\ce{BaSO4}]} = \\ = \sqrt{\pu{1,08E-10 mol2 dm-6}}

[\ce{Ba^{2+}}] = \pu{1,04E-5 mol dm-3}

Korak 3

\ce{BaF2(s) <=>[H2O] Ba^{2+}(aq) + 2F-(aq)} Koncentracija u ravnoteži: [\ce{Ba^{2+}}] = x \quad [\ce{F-}] = 2x

K_{\textrm{s}}(\ce{BaF2}) = [\ce{Ba^{2+}}][\ce{F-}]^{2}

K_{\textrm{s}}(\ce{BaF2}) = x\cdot (2x)^{2}

K_{\textrm{s}}(\ce{BaF2}) = 4x^{3}

x = [\ce{Ba^{2+}}] = \sqrt[3]{\dfrac{{K_{\textrm{s}}[\ce{BaF2}]}}{4}}

= \sqrt[3]{\dfrac{\pu{1,84E-7 mol3 dm-9}}{4}} =

= \pu{3,58E-3 mol dm-3}

Odgovor:

Koncentracija (c) barijevih iona (Ba2+) u zasićenoj otopini barijeva fluorida (BaF2) je veća (>) od koncentracije (c) barijevih iona (Ba2+) u zasićenoj otopini barijeva sulfata (BaSO4).
Stoga, veća (>) je topljivost barijeva fluorida (BaF2).

Riješeni primjer 1

Koja je sol topljivija u vodi, barijev sulfat ili barijev fluorid?

Ravnotežna konstanta otapanja barijeva sulfata je \pu{1,08E-10 mol2 dm-6} , a barijeva fluorida je \pu{1,84E-7 mol3 dm-9} pri 25 °C.

Zadano je:

K_{\textrm{s}}(\ce{BaSO4}) = \pu{1,08E-10 mol2 dm-6}
K_{\textrm{s}}(\ce{BaF2}) = \pu{1,84E-7 mol3 dm-9}

Traži se:

c_{1}(\ce{Ba^{2+}, aq}) = ?
c1– koncentracija barijevih iona u otopini \ce{BaSO4}

c_{2}(\ce{Ba^{2+},aq}) = ?
c2 – koncentracija barijevih iona u otopini \ce{BaF2}

Izradak:

Iz vrijednosti ravnotežne konstante otapanja soli može se izračunati koncentracija barijevih iona u vodenoj otopini jedne i druge soli.

Korak 1

Jednadžba disocijacije barijeva sulfata u vodi:   , a ravnotežne koncentracije barijevih i sulfatnih iona označe se sa  x .

\ce{BaSO4(s) <=>[H2O] Ba^{2+}(aq) + SO4^{2-}(aq)}

Ravnotežne koncentracije barijevih i sulfatnih iona su jednake i označe se sa X .

x = [\ce{Ba^{2+}}] = [\ce{SO4^{2-}}]

Korak 2

Iz izraza za ravnotežnu konstantu otapanja soli može se izračunati množinska koncentracija barijevih iona:

K_{\textrm{s}}(\ce{BaSO4}) = [\ce{Ba^{2+}}] [\ce{SO4^{2-}}]

K_{\textrm{s}}[\ce{BaSO4}] = x\cdot x

K_{\textrm{s}}[\ce{BaSO4}] = x^2

x = [\ce{Ba^{2+}}] = \sqrt{K_{\textrm{s}}[\ce{BaSO4}]} \\ = \sqrt{\pu{1,08E-10 mol2 dm-6}}

[\ce{Ba^{2+}}] = \pu{1,04E-5 mol dm-3}

Korak 3

\ce{BaF2(s) <=>[H2O] Ba^{2+}(aq) + 2F-(aq)}

Koncentracija u ravnoteži:

[\ce{Ba^{2+}}] = x

[\ce{F-}] = 2x

K_{\textrm{s}}(\ce{BaF2}) = [\ce{Ba^{2+}}][\ce{F-}]^{2}

K_{\textrm{s}}(\ce{BaF2}) = x\cdot (2x)^{2}

K_{\textrm{s}}(\ce{BaF2}) = 4x^{3}

x = \sqrt[3]{\dfrac{{K_{\textrm{s}}[\ce{BaF2}]}}{4}} = \sqrt[3]{\dfrac{\pu{1,84E-7 mol3 dm-9}}{4}}

x = \pu{3,58E-3 mol dm-3}

Odgovor:

S obzirom na to da je koncentracija barijevih iona, u zasićenoj vodenoj otopini barijeva fluorida, veća od koncentracije barijevih iona, u zasićenoj vodenoj otopini barijeva sulfata, topljivost barijeva fluorida je veća.

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Ravnotežna konstanta otapanja (Ks) magnezijeva karbonata (\ce{MgCO3}) je 6,82×10−6 mol2 dm−6 pri 25 °C.

Ravnotežna konstanta otapanja (Ks) kalcijeva karbonata (\ce{CaCO3}) je 3,36×10−9 mol2 dm−6 pri 25 °C.

Koja je sol topljivija u vodi?

Ako su mjerne jedinice ravnotežnih konstanti otapanja (Ks) soli jednake (=), topljivija je ona sol čija je vrijednost konstante veća (>).

Prema tome iz navedenih primjera može se isčitati da se u vodi bolje otapa

.

Navedenu pretpostavku potvrdite izračunom vrijednosti koncentracija (c) magnezijevih ( \ce{Mg^{2+}}) i kalcijevih iona ( \ce{Ca^{2+}}) u zasićenim vodenim otopinama navedenih soli.

c (\ce{Mg^{2+}(aq)}) =

\pu{E-3 mol dm-3}

c (\ce{Ca^{2+}(aq)}) =

\pu{E-5 mol dm-3}

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Izračunajte ravnotežnu konstantu otapanja (Ks) olovova (II) jodida (PbI2).

Množinska koncentracija (c) olovovih (II) iona (Pb2+) u otopini iznosi 1,27×10−3 mol dm−3.

c (\ce{Pb2+} ) = \pu{1,27E-3 mol dm-3}
Ks  (\ce{PbI2} ) = ?

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Koja je sol topljivija u vodi, litijev karbonat ( \ce{Li2CO3} ) ili litijev fosfat ( \ce{Li3PO4} ) ?
Ravnotežna konstanta otapanja (Ks) litijeva karbonata ( \ce{Li2CO3} ) je \pu{8,15E-4 mol3 dm-9} pri 25 °C.
Ravnotežna konstanta otapanja (Ks) litijeva fosfata ( \ce{Li3PO4} ) je \pu{2,37E-4 mol4 dm-12} pri 25 °C.
Izračunajte koncentracije (c) litijevih iona (Li+) u obje soli.
Rezultate upišite kao decimalni broj.
Ime soli upišite riječima.

Ks ( \ce{Li2CO3} ) = 8,15 × 10-4 mol3 dm-9
Ks ( \ce{Li3PO4} ) = 2,37 × 10-4 mol4 dm-12

c ( \ce{Li+, Li2CO3} ) = ?
c( \ce{Li+, Li3PO4} ) = ?

c(\ce{Li+}, \ce{Li2CO3}) =

mol dm-3

c(\ce{Li+}, \ce{Li3PO4}) =

mol dm-3

Topljivija sol u vodi je

.

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Ravnotežna konstanta otapanja magnezijeva karbonata je \pu{6,82E-6 mol2 dm-6} , a kalcijeva karbonata \pu{3,36E-9 mol2 dm-6} pri 25 °C. Koja je sol topljivija u vodi?

Ako su mjerne jedinice ravnotežnih konstanti otapanja soli jednake, topljivija je ona sol čija je vrijednost konstante veća.

Prema tome iz navedenih primjera može se isčitati da se u vodi bolje otapa

.

Navedenu pretpostavku potvrdite izračunom vrijednosti koncentracija magnezijevih i kalcijevih iona u zasićenim vodenim otopinama navedenih soli.

c(\ce{Mg^{2+}, aq}) =
\pu{E-3 mol dm-3}
c(\ce{Ca^{2+}, aq}) =
\pu{E-5 mol dm-3}
Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Izračunajte ravnotežnu konstantu otapanja olovova(II) jodida ako je množinska koncentracija olovovih(II) iona u otopini \pu{1,27E-3 mol dm-3} .

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Koja je sol topljivija u vodi, litijev karbonat ili litijev fosfat?

Ravnotežna konstanta otapanja litijeva karbonata je \pu{8,15E-4 mol3 dm-9} , a litijeva fosfata je \pu{2,37E-4 mol4 dm-12}
pri 25 °C. Izračunajte koncentracije litijevih iona u obje soli. Rezultate upišite kao decimalni broj, a ime soli riječima.

Rješenje:

c(\ce{Li+}, \ce{Li2CO3}) =
mol dm-3
c(\ce{Li+}, \ce{Li3PO4}) =
mol dm-3
Topljivija sol u vodi je
.
Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Dobivanje soli

Soli se mogu dobiti na različite načine:

Primjer:

1. Dobivanje soli izravnom sintezom iz elemenata:

metal + nemetal  \rightarrow  sol

Primjer:

\ce{2Fe(s) + 3Cl2(g) -> 2FeCl3(s)}

Dobivanje soli

Soli se mogu dobiti na različite načine.

1. Dobivanje soli izravnom sintezom iz elemenata:

metal + nemetal \rightarrow sol

Primjer:

\ce{2Fe(s) + 3Cl2(g) -> 2FeCl3(s)}

2. Dobivanje soli reakcijom metala i kiseline:

metal + kiselina  \rightarrow  sol + vodik

Primjer:

\ce{Zn(s) + 2HCl(aq) -> ZnCl2(aq) + H2(g)}

2. Dobivanje soli reakcijom metala i kiseline:

metal + kiselina \rightarrow sol + vodik

Primjer:

\ce{Zn(s) + 2HCl(aq) -> ZnCl2(aq) + H2(g)}

3. Dobivanje soli reakcijom neutralizacije:

a) baza + kiselina \rightarrow  sol + voda

Primjer:

\ce{2NaOH(aq) + H2SO4(aq) -> Na2SO4(aq) + 2H2O(l)}

Sumporna kiselina (H2SO4) je diprotonska kiselina, ionizira u dva stupnja.

Stoga se i reakcija neutralizacije sumporne kiseline (H2SO4) s natrijevom lužinom (NaOH) odvija u dva stupnja:

I. stupanj

\ce{NaOH(aq)} \ce{+} \ce{H2SO4(aq) -> NaHSO4(aq) + H2O(l)}
↓
natrijev hidrogensulfat

II. stupanj

\ce{NaOH(aq)} \ce{+} \ce{NaHSO4(aq)} \ce{-> Na2SO4(aq) + H2O(l)}
↓
natrijev sulfat

Zbirna reakcija:

\ce{2NaOH(aq) + H2SO4(aq) -> Na2SO4(aq) + 2H2O(l)}

U vodenim otopinama neutralizacija je reakcija oksonijevih i hidroksidnih iona:

\ce{H3O+(aq) + OH-(aq) <=> 2H2O(l)} .

3. Dobivanje soli reakcijom neutralizacije:

a) baza + kiselina \rightarrow sol + voda

Primjer:

\ce{2NaOH(aq) + H2SO4(aq) -> Na2SO4(aq) + 2H2O(l)}

Sumporna kiselina je diprotonska kiselina, ionizira u dva stupnja pa se i reakcija neutralizacije sumporne kiseline s natrijevom lužinom odvija u dva stupnja:

I. stupanj

\ce{NaOH(aq)} \ce{+} \ce{H2SO4(aq) -> NaHSO4(aq) + H2O(l)}
↓
natrijev hidrogensulfat

II. stupanj

\ce{NaOH(aq)} \ce{+} \ce{NaHSO4(aq)} \ce{-> Na2SO4(aq) + H2O(l)}
↓
natrijev sulfat

Zbirna reakcija:

\ce{2NaOH(aq) + H2SO4(aq) -> Na2SO4(aq) + 2H2O(l)}

U vodenim otopinama neutralizacija je reakcija oksonijevih i hidroksidnih iona:

\ce{H3O+(aq) + OH-(aq) <=> 2H2O(l)} .

Kiselo-bazne titracije

Kiselo-bazna titracija je volumetrijska metoda kvantitativne kemijske analize kojom se može odrediti koncentracija neke kiseline ili lužine.

Kiselo-bazne titracije

Kiselo-bazna titracija je volumetrijska metoda kvantitativne kemijske analize kojom se može odrediti koncentracija neke kiseline ili lužine.

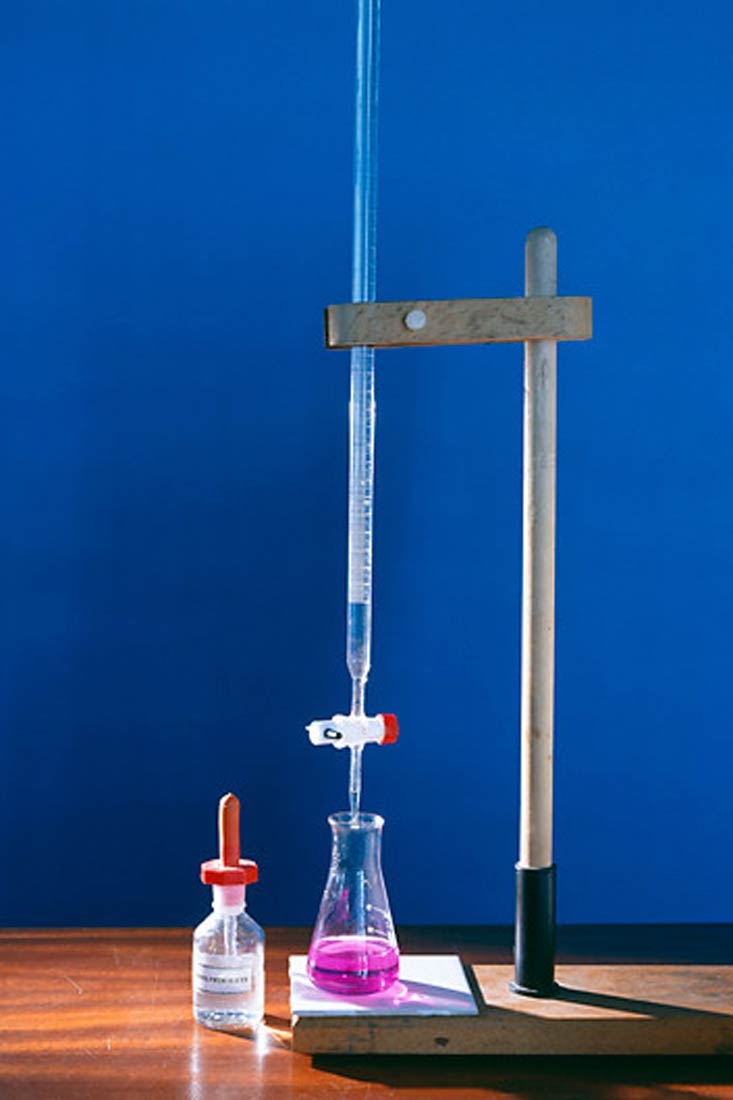
Aparatura za titraciju
Aparatura za titraciju

Određivanje se izvodi na način da se biretom otopina poznate koncentracije dodaje otopini nepoznate koncentracije kojoj je dodan indikator.
Ovaj postupak naziva se titracija.
Otopina koja se dodaje biretom naziva se titrans.
Titrirana otopina naziva se analit.
Točka ekvivalencije označava trenutak kad je u otopinu, koja se titrira, dodana ekvivalentna množina tvari kojom titriramo.
Promjena boje indikatora ne događa se točno u točki ekvivalencije.
Promjena boje indikatora određuje točku završetka titracije.

Određivanje se izvodi na način da se biretom dodaje otopina poznate koncentracije otopini nepoznate koncentracije kojoj je dodan indikator.

Otopina u bireti naziva se titrant, a titrirana otopina analit.

Točka ekvivalencije označava trenutak kad je u otopinu, koju se titrira, dodana ekvivalentna množina tvari kojom titriramo.

Promjena boje indikatora ne događa se točno u točki ekvivalencije i određuje točku završetka titracije.

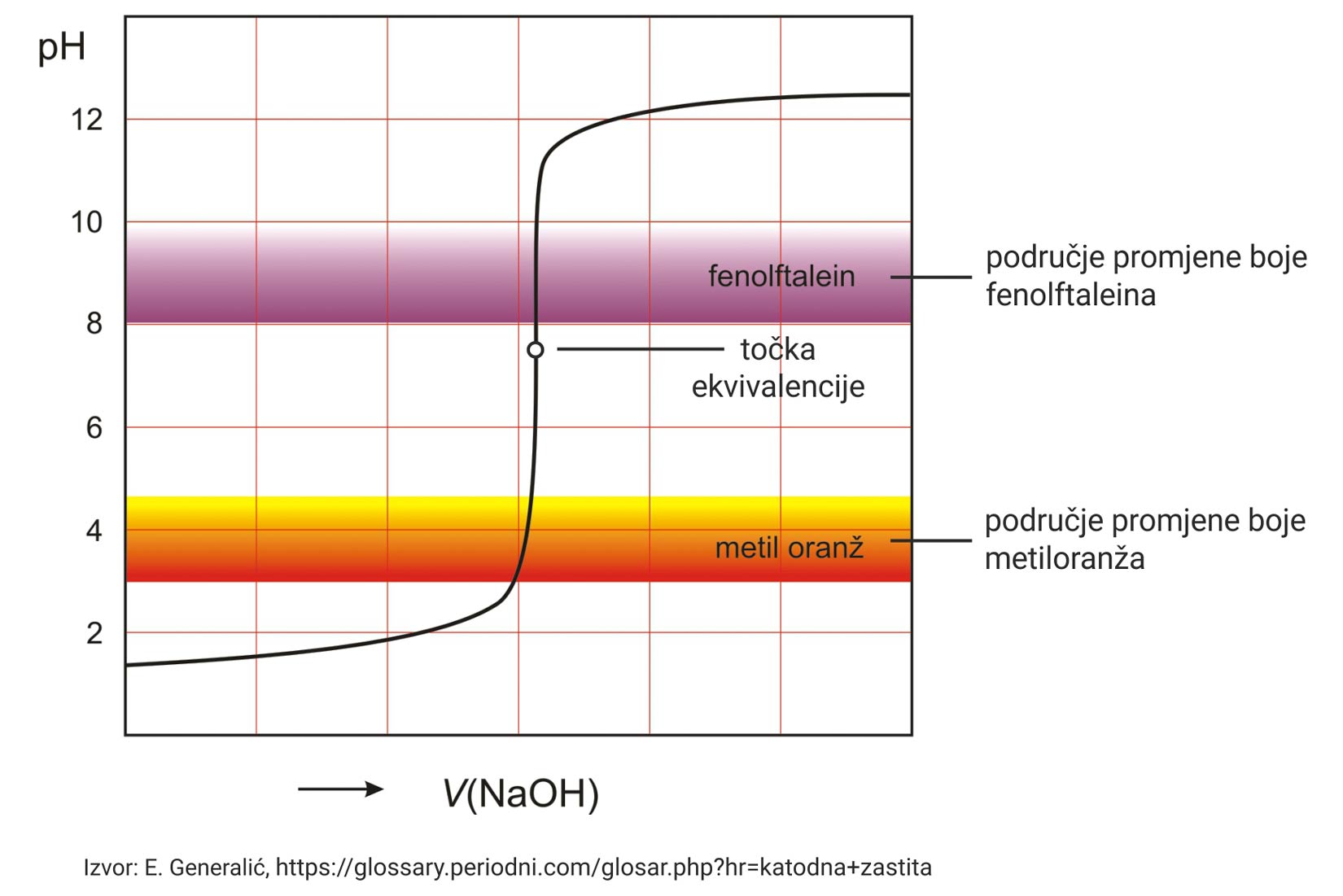
Krivulja titracije jake kiseline jakom lužinom
Krivulja titracije jake kiseline jakom lužinom

Iz titracijske je krivulje vidljivo da se pH-vrijednost naglo mijenja u blizini točke ekvivalencije.

Za titraciju jakih kiselina i jakih baza kao indikator se najčešće koriste:

  1. fenolftalein,
  2. metiloranž,
  3. metilno crvenilo.

Iz titracijske je krivulje vidljivo da se pH-vrijednost naglo mijenja u blizini točke ekvivalencije. Za titraciju jakih kiselina i jakih baza kao indikator se najčešće koriste fenolftalein, metiloranž i metilno crvenilo.

Riješeni primjer 2.

Odpipetira se 20 mL otopine klorovodične kiseline nepoznate koncentracije koja se ispusti u Erlenmeyerovu tikvicu i nakon toga se doda nekoliko kapi  fenolftaleina. U kiselinu se zatim, polagano, kap po kap, iz birete dodaje kalijeva lužina množinske koncentracije 0,10 mol  L –1 do promjene boje indikatora. Ako se za titraciju utroši 20 mL kalijeve lužine, izračunajte množinsku  koncentraciju klorovodične kiseline.

Zadano je:


V(\ce{HCl}) = \pu{20 mL}

c(\ce{KOH}) = \pu{0,10 mol L-1}

V(\ce{KOH}\textrm{, utrošenog za neutralizaciju}) = \pu{20 mL}

Traži se: 

c(\ce{HCl}) = ?

Izradak:

Titracija se temelji na reakciji neutralizacije jake lužine s jakom kiselinom prema sljedećoj jednadžbi kemijske reakcije:


\ce{HCl(aq) + KOH(aq) -> KCl(aq) + H2O(l)}

Na temelju jednadžbe kemijske reakcije može se zaključiti da su množine klorovodične kiseline i kalijeve lužine jednake.

n(\textrm{kiseline}) = n(\textrm{lužine})

c(\ce{HCl})V(\ce{HCl}) = c(\ce{KOH})V(\ce{KOH})

c(\ce{KOH}) = \dfrac{c(\ce{HCl})V(\ce{HCl})}{V(\ce{KOH})}

c(\ce{HCl}) = \dfrac{\pu{0,100 mol L-1}\pu{0,020 L}}{\pu{0,020 L}} = \pu{0,10 mol L-1}

Odgovor:

Množinska koncentracija klorovodične kiseline je 0,10 mol L–1.

Odredite koncentracije otopina klorovodične kiseline (HCl) na isti način u sljedećim primjerima tako da riješite interaktivni zadatak.

Odredite koncentracije otopina klorovodične kiseline na isti način u sljedećim primjerima tako da riješite interaktivni zadatak.

Neutralizacija je i reakcija bazičnog oksida i kiseline, kiselog oksida i baze, kao i bazičnog i kiselog oksida:
 
b) bazični oksid + kiselina \rightarrow sol + voda
 

\ce{CaO(s) + 2HNO3(aq) -> Ca(NO3)2(aq) + H2O(l)}

 
c) kiseli oksid + baza \rightarrow sol + voda
 
\ce{CO2(g) + 2NaOH(aq) -> Na2CO3(s) + H2O(l)}

 
d) bazični oksid + kiseli oksid \rightarrow sol
 
\ce{CaO(s) + SO2(g) -> CaSO3(s)}
 
4. Dobivanje soli reakcijom dvostruke izmjene iona:
 
sol1 + sol2 \rightarrow sol3 + sol4
 
Soli vrlo slabe topljivosti dobivaju se reakcijom dvostruke izmjene, taloženjem.

Primjer:
 

\ce{2KI(aq) + Pb(NO3)2(aq) -> PbI2(s) + 2KNO3(aq)}

 

Hidroliza soli

Jesu li vodene otopine soli neutralne otopine?

Pogledajte sljedeći videozapis.

Donesite zaključak o pH-vrijednosti vodenih otopina nekih soli.

Hidroliza soli

Jesu li vodene otopine soli neutralne otopine? Pogledajte sljedeći videozapis i potom donesite zaključak o pH-vrijednosti vodenih otopina nekih soli.

U navedenim reakcijama ioni soli reagiraju s molekulama vode pa takvu vrstu protolitičkih reakcija nazivamo hidroliza soli.
S vodom reagiraju samo kiselinski anioni slabih kiselina (konjugirane jake baze) ili kationi slabih baza (konjugirane jake kiseline).
Anioni jakih kiselina i kationi jakih baza ne reagiraju s molekulama vode.
Dolazi samo do hidratacije navedenih iona.

Otopina natrijeva klorida (NaCl) je neutralna jer otapanjem u vodi nastaju hidratizirani natrijevi (Na+) i kloridni (Cl–) ioni.
Ti ioni ne reagiraju s vodom.
U vodi se ne mijenja koncentracija (c) oksonijevih, H3O+ i hidroksidnih, OH– iona.
Prema tome, pH nastale otopine je 7.

\ce{NaCl(s) ->[H2O] Na+(aq) + Cl-(aq)}

S vodom reagiraju samo anioni slabih kiselina (konjugirane jake baze) ili kationi slabih baza (konjugirane jake kiseline).

Otapanjem natrijeva cijanida (NaCN) u vodi, nastaju natrijevi (Na+) i cijanidni (CN–) ioni koji u reakciji s vodom povećavaju koncentraciju (c) hidroksidnih (OH–) iona.


\ce{NaCN(s) ->[H2O] Na+(aq) + CN-(aq)}

\ce{CN-(aq) + H2O -> HCN(aq) + OH-(aq)}


Vodena otopina je lužnata, \textrm{pH} > 7 .

Otapanjem amonijeva acetata (CH3COONH4) u vodi nastaju amonijevi (NH4+) i acetatni (CH3COO–) ioni.
Amonijevi ioni u reakciji s vodom povećavaju koncentraciju (c) oksonijevih iona (H3O+).
Acetatni ioni u reakciji s vodom povećavaju koncentraciju (c) hidroksidnih iona (OH–).
Prema tome je pH vodene otopine približno 7.
Točna vrijednost pH ovisi o vrijednostima konstanti disocijacije octene kiseline, Ka i amonijaka, Kb.


\ce{CH3COONH4(s) ->[H2O] NH4+(aq) + CH3COO-(aq)}

\ce{NH4+(aq) + H2O(l) -> NH3(aq) + H3O+(aq)}

\ce{CH3COO-(aq) + H2O(l) -> CH3COOH(aq) + OH-(aq)}

\ce{H3O+(aq) + OH-(aq) -> 2H2O(l)}


 

U navedenim primjerima ioni soli reagiraju s molekulama vode pa takvu vrstu protolitičkih reakcija nazivamo hidroliza soli.

Anioni jakih kiselina i kationi jakih baza ne reagiraju s molekulama vode, već dolazi samo do hidratacije navedenih iona.

\ce{NaCl(s) ->[H2O] Na+(aq) + Cl-(aq)}

Otopina natrijeva klorida je neutralna jer otapanjem u vodi nastaju hidratizirani natrijevi, ( \ce{Na+} ), i kloridni, ( \ce{Cl-} ), ioni. Ti ioni ne reagiraju s vodom, pa se u vodi ne mijenja koncentracija oksonijevih, \ce{H3O+} , i hidroksidnih, \ce{OH-} , iona. Stoga je pH-vrijednost nastale otopine 7.

S vodom reagiraju samo anioni slabih kiselina (konjugirane jake baze) ili kationi slabih baza (konjugirane jake kiseline).

Otapanjem natrijeva cijanida u vodi osim natrijevih nastaju i cijanidni ioni, jake konjugirane baze. Prema tome cijanidni ioni su proton akceptori te u reakciji s vodom povećavaju koncentraciju hidroksidnih iona.

\ce{NaCN(s) ->[H2O] Na+(aq) + CN-(aq)}

\ce{CN-(aq) + H2O(l) <=> HCN(aq) + OH-(aq)}

Vodena otopina natrijeva cijanida je lužnata, \textrm{pH} > 7 .

Otapanjem amonijeva acetata u vodi nastaju amonijevi i acetatni ioni. Amonijevi ioni u reakciji s vodom povećavaju koncentraciju oksonijevih iona, a acetatni hidroksidnih iona.

\ce{CH3COONH4(s) ->[H2O] NH4+(aq) + CH3COO-(aq)}

\ce{NH4+(aq) + H2O(l) <=> NH3(aq) + H3O+(aq)}

\ce{CH3COO-(aq) + H2O(l) <=> CH3COOH(aq) + OH-(aq)}

\ce{H3O+(aq) + OH-(aq) <=> 2H2O(l)}

Prema tomu pH-vijednost vodene otopine amonijeva acetata približno je 7.

Riješeni primjer 3

Izračunajte množinsku koncentraciju (c) amonijeva klorida ( \ce{NH4Cl} ).
pH otopine iznosi 4,83.
Konstanta disocijacije baze, Kb ( \ce{NH3} ) iznosi \pu{1,8E-5 mol dm-3} .

Zadano je:
 
pH = 4,83
 
K_{b}(\ce{NH3}) = \pu{1,8E-5 mol dm-3}
 
Traži se:
 
c(\ce{NH4Cl}) = ?

Izradak:

Korak 1.

Amonijev klorid ( \ce{NH4Cl} ) je topljiva sol koja u vodi disocira na amonijeve, NH4+, i kloridne, Cl– ione.

\ce{NH4Cl(s) ->[H2O] NH4+(aq) + Cl-(aq)}

Nastali \ce{NH4+} ioni protolitički reagiraju s vodom.

Hidroliza amonijeva iona:

\ce{NH4+(aq)} + \ce{H2O(l)} \ce{<=>} \ce{NH3(aq)} + \ce{H3O+(aq)}
↓ ↓ ↓ ↓
kiselina 1 baza 1 baza 2 kiselina 2


natrijev hidrogensulfatnatrijev hidrogensulfat
U reakciji hidrolize amonijev ( \ce{NH4+} ) ion je kiselina.
Stoga je konstanta Ka(( \ce{NH4+} \) ) :

K_{a}(\ce{NH4+}) = \dfrac{c(\ce{NH3})c(\ce{H3O+})}{c(\ce{NH4+})}

Budući je zadana K_{b}(\ce{NH3}) , slijedi:

K_{a}(\ce{NH4+}) = \dfrac{K_{w}}{K_{b}(\ce{NH3})}

c (\ce{H+} )⋅ c (\ce{OH−} ) = K_\textrm{w} = \pu{10−14 mol2/dm6}

[\ce{H+} ] \cdot [ \ce{OH−}] = K_\textrm{w} = \pu{10−14 mol2 dm−6}

K_{a}(\ce{NH4+}) = \dfrac{10^{-14}\pu{mol2 dm-6}}{\pu{1,8E-5 mol dm-3}}

K_{a}(\ce{NH4+}) = \pu{5,6E-10 mol dm-3}

Iz vrijednosti pH otopine soli izračuna se koncentracija oksonijevih iona, c( \ce{H3O+} ):


\textrm{pH} = -\log \dfrac{c(\ce{H3O+})}{\pu{mol dm-3}}
c (\ce{H3O+}) = \pu{10-pH = 10-4,83}
c (\ce{H3O+}) = \pu{1,48 × 10-5 mol dm-3}

Ravnotežne koncentracije amonijaka ( \ce{NH4+} ) i oksonijevih iona ( \ce{H3O+} ) unesu se u tablicu:

\ce{NH4+(aq) + H2O(l) <=> NH3(aq) + H3O+(aq)}

\ce{NH4+(aq)} \ce{NH3(aq)} \ce{H3O+(aq)}
početna koncentracija/ mol dm–3 ? 0 0
promjena -x +x +x
ravnotežna koncentracija/ mol dm–3 ? \pu{1,48E-5} \pu{1,48E-5}


 

Iz izraza za konstantu Ka sada se može izračunati koncentracija (c) amonijevih iona ( \ce{Nh4+} ).

K_{a}(\ce{NH4+}) = \dfrac{c(\ce{NH3})c(\ce{H3O+})}{c(\ce{NH4+})}
c(\ce{NH4+}) = \dfrac{c(\ce{NH3})c(\ce{H3O+})}{K_{a}(\ce{NH4+})}

c(\ce{NH4+}) = \dfrac{(\pu{1,48E-5 mol dm-3})^{2}}{\pu{5,6E-10 mol dm-3}}
c(\ce{NH4+}) = \pu{0,39 mol dm-3}

Budući da je amonijev klorid ( \ce{NH4Cl} ) sol dobro topljiva u vodi, koncentracija (c) amonijevih iona ( \ce{NH4+} ) jednaka (=) je koncentraciji (c) amonijeva klorida ( \ce{NH4Cl} ).
c (\ce{NH4+}) = c (\ce{NH4Cl})

Odgovor: Množinska koncentracija (c) amonijeva klorida ( \ce{NH4Cl} ) u otopini, čiji je pH = 4,83 je \pu{0,39 mol dm-3} .

Riješeni primjer 3

Izračunajte množinsku koncentraciju amonijeva klorida ako je pH-vrijednost vodene otopine 4,83, a konstanta ionizacije baze, K_{\textrm{b}}(\ce{NH3}) = \pu{1,8E-5 mol dm-3} .

Zadano je:
 
pH = 4,83
 
K_{\textrm{b}}(\ce{NH3}) = \pu{1,8E-5 mol dm-3}
 
Traži se:

c(\ce{NH4Cl}) = ?

Izradak:

Korak 1.

Amonijev klorid je topljiva sol koja u vodi disocira na amonijeve, \ce{NH4+} i kloridne, \ce{Cl-} ione.

\ce{NH4Cl(s) ->[H2O] NH4+(aq) + Cl-(aq)}

Nastali \ce{NH4+} ioni protolitički reagiraju s vodom.

Hidroliza amonijeva iona:
 

\ce{NH4+(aq)} + \ce{H2O(l)} \ce{<=>} \ce{NH3(aq)} + \ce{H3O+(aq)}
↓ ↓ ↓ ↓
kiselina 1 baza 1 baza 2 kiselina 2


 
U reakciji hidrolize \ce{NH4+} ion je kiselina, pa je konstanta K_{\textrm{a}} (\ce{NH4+}) :
 
K_{\textrm{a}}(\ce{NH4+}) = \dfrac{c(\ce{NH3})c(\ce{H3O+})}{c(\ce{NH4+})}
 
Budući je zadana K_{\textrm{b}}(\ce{NH3}) , slijedi:
 
K_{\textrm{a}}(\ce{NH4+}) = \dfrac{K_{w}}{K_\textrm{b}(\ce{NH3})}
 
K_{\textrm{a}}(\ce{NH4+}) = \dfrac{10^{-14}\pu{mol2 dm-6}}{\pu{1,8E-5 mol dm-3}}
 
K_{\textrm{a}}(\ce{NH4+}) = \pu{5,6E-10 mol dm-3}

Ravnotežne koncentracije amonijaka i oksonijevih iona unesu se u tablicu:

\ce{NH4+(aq) + H2O(l) <=> NH3(aq) + H3O+(aq)}

Tablica 1. Ravnotežne koncentracije 
c(\ce{NH4+}) c(\ce{NH3}) c(\ce{H3O+})
početna koncentracija/

mol dm–3

 ? 0 0
promjena -x +x +x
ravnotežna koncentracija/

mol dm–3

 ? \pu{1,48E-5} \pu{1,48E-5}


 
Iz izraza za konstantu K_{\textrm{a}} sada se može izračunati koncentracija amonijevih iona.
 
K_{\textrm{a}}(\ce{NH4+}) = \dfrac{c(\ce{NH3})c(\ce{H3O+})}{c(\ce{NH4+})}
 
c(\ce{NH4+}) = \dfrac{c(\ce{NH3})c(\ce{H3O+})}{K_{\textrm{a}}(\ce{NH4+})}
 
c(\ce{NH4+}) = \dfrac{(\pu{1,48E-5 mol dm-3})^{2}}{\pu{5,6E-10 mol dm-3}}
 
c(\ce{NH4+}) = \pu{0,39 mol dm-3}
 
Budući da je amonijev klorid sol dobro topljiva u vodi, koncentracija amonijevih iona jednaka je koncentraciji amonijeva klorida.

Odgovor: Množinska koncentracija amonijeva klorida u otopini čiji je pH = 4,83 je \pu{0,39 mol dm-3} .

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte pH otopine amonijeva klorida (NH4Cl) množinske koncentracije (c) 0,10 mol dm-3.
Konstanta disocijacije baze, Kb (NH3) iznosi 1,8 × 10-5 mol dm-3.

K_{b}(\ce{NH3}) = \pu{1,8E-5 mol dm-3}
c (\ce{NH4Cl}) = \pu{0,10 mol dm-3}
pH = ?

pH =

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Je li vodena otopina navedenih soli kisela, lužnata ili neutralna.
Upišite odgovarajući pojam:

 

cinkov nitrat ( \ce{Zn(NO3)2} )

stroncijev nitrat ( \ce{Sr(NO3)2} )

kalijev cijanid ( \ce{KCN} )

amonijev hidrogensulfid ( \ce{NH4HSO3} )

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte pH-vrijednost otopine amonijeva klorida množinske koncentracije \pu{0,10 mol dm-3} , ako je konstanta disocijacije baze, K_{\textrm{b}}(\ce{NH3}) = \pu{1,8E-5 mol dm-3} .

Rješenje:

pH =
Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Vodena otopina navedenih soli je kisela, lužnata ili neutralna. Upišite odgovarajući pojam:

cinkov nitrat;
stroncijev nitrat;
kalijev cijanid;
amonijev hidrogensulfid;
Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Istraži - Kompleksni spojevi

Svaki kompleksni spoj sastoji se od centralnog metalnog iona i liganada - iona ili molekula koji se vežu na centralni ion. Vezanjem liganada popunjavaju se prazne ili polupopunjene s, p i d –orbitale.

Na kraju…

Razmislite i odgovorite na pitanja!

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Koja vodena otopina soli ima najmanju pH-vrijednost?

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Odredite je li otopina soli kisela, bazična ili neutralna:
 
\ce{NaBr(aq)}


\ce{NaHS(aq)}

\ce{NH4Br(aq)}

\ce{Na2HPO4(aq)}

Netočno
Točno

Klikom odaberite jedan ili više točnih odgovora.

Odaberite sve točne odgovore.

U kojim otopinama nastane bijeli talog?

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Ako se u otopinu kalijeva jodida (KI) ulije otopina olovova (II) nitrata (Pb(NO3)2), u suvišku nastaje žuti talog.
Nakon filtriranja i sušenja masa nastalog taloga iznosi 6,50 grama (m).
Izračunajte masu (m) kalijeva jodida (KI) u početnoj otopini.

m (talog) = 6,50 g
m (KI) = ?

Rješenje:

m(\ce{KI}) =

g

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Odredite je li otopina amonijeva fluorida , \ce{NH4F} kisela, bazična ili neutralna, ako je:
 
K_{a}(\ce{NH4+}) = \pu{5,6E-10 mol dm-3} ,
K_{b}(\ce{F-}) = \pu{1,4E-11 mol dm-3} .
 
Otopina amonijeva fluorida \ce{NH4F} kisela, jer je:

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Koja vodena otopina soli ima najmanju pH-vrijednost?

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Odredite je li otopina soli kisela, bazična ili neutralna:

\ce{NaBr(aq)} ;
\ce{NaHS(aq)} ;
\ce{NH4Br(aq)} ;
\ce{Na2HPO4(aq)} ;
Netočno
Točno

Klikom odaberite jedan ili više točnih odgovora.

Odaberite sve točne odgovore.

U kojim otopinama nastane bijeli talog?

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Ako se u otopinu kalijeva jodida ulije otopina olovova(II) nitrata u suvišku nastaje žuti talog. Nakon filtriranja i sušenja masa nastalog taloga iznosi 6,50 g. Izračunajte masu kalijeva jodida u početnoj otopini.

Rješenje:

m(\ce{KI}) =
g
Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Za otopina amonijeva fluorida, \ce{NH4F} vrijedi da je K_{\textrm{a}}(\ce{NH4+}) = \pu{5,6E-10 mol dm-3} , a K_{\textrm{b}}(\ce{F-}) = \pu{1,4E-11 mol dm-3} . Otopina amonijeva fluorida je stoga kisela, jer je:

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?