Matematika 1 - Aktivnosti za samostalno učenje

Na početku...

Svi znamo čemu služe kalendari. No, znate li da se u kalendarima kriju magični trikovi? Evo jednog od njih. Pogledajte kalendar na slici. Na kalendaru ćemo odabrati četiri broja smještena u kvadrat $2 \times 2 .$ Na primjer, to mogu biti brojevi $11,$ $12,$ $18$ i $19 .$ Odaberite svoja četiri broja. Zbrojite ih. Upišite zbroj na predviđeno mjesto. Računalo će pogoditi koje ste brojeve odabrali. Je li pogodak slučajnost? Pokušajte još jedanput.

Pogledajte raspored brojeva u kalendaru. Uočavate li pravilnost? Objasnite kako je računalo pogodilo vaše brojeve.

Brojevi su u kalendaru raspoređeni tako da se u redcima povećavaju za $1,$ a u stupcima za $7 .$ To će nam svojstvo kalendara pomoći u objašnjavanju magičnog trika.

Pogledajmo, na primjer, brojeve $11,$ $12,$ $18$ i $19 .$ Prvi od njih je $11 .$ Možemo li s pomoću njega zapisati ostale brojeve?

$12 = 11 + 1$

$18 = 11 + 7$

$19 = 11 + 8$

Označimo broj u gornjem lijevom kutu odabranog kvadrata brojeva s $x .$ Zapišimo s pomoću njega ostale brojeve odabranog kvadrata. To su:

$x + 1, x + 7, x + 8 .$

Zbrojimo sva četiri broja:

$S = x + (x + 1) + (x + 7) + (x + 8) = 4 x + 16 .$

Taj smo zbroj izračunali. Ako je poznat zbroj, prvi zamišljeni broj može se izračunati ovako:

$x = \frac{S - 16}{4} .$

Zatim se s pomoću njega mogu dodavanjem brojeva $1,$ $7$ i $8$ izračunati ostali.

Zadatak 1.

U kalendaru se kriju i drugi magični trikovi. Otkrijte i objasnite neke od njih.

Odaberite u kalendaru četiri broja u kvadratu $2 x 2 .$ Pomnožite broj u gornjem desnom kutu kvadrata s brojem u donjem lijevom kutu. Od tog umnoška oduzmite umnožak broja u gornjem lijevom i donjem desnom kutu. Zapišite rezultat u bilježnicu. Ponovite s nekim drugim kvadratima. Zapišite zaključak. Objasnite.
Zamolite prijatelja da u kalendaru odabere pet brojeva smještenih u obliku slova T (na primjer $8,$ $9,$ $10,$ $16,$ $23$ ). Pronađite magični trik s pomoću kojega možete pogoditi odabrane brojeve.
Smislite neki svoj magični trik s brojevima u kalendaru.

Razlika je uvijek jednaka $7 .$ Označimo li brojeve kao u prethodnom triku, razliku računamo ovako:

$(x + 1) (x + 7) - x (x + 8) = x^{2} + x + 7 x + 7 - x^{2} - 8 x = 7 .$
Označite neki od odabranih brojeva s $x$ i ostale brojeve zapišite s pomoću tog broja.

Parcijalni razlomci

Kolekcija zadataka 1

Zadatak 2.

U ovom ste modulu naučili računati s algebarskim razlomcima. Zbrojite algebarske razlomke $\frac{2}{x - 1}$ i $\frac{5}{x + 4} .$

$\frac{2}{x - 1} + \frac{5}{x + 4} = \frac{2 (x + 4) + 5 (x - 1)}{(x - 1) (x + 4)} = \frac{7 x + 3}{(x - 1) (x + 4)}$

Zadatak 3.

Pogledajmo sada obratni postupak. Zadan je algebarski razlomak koji je dobiven kao zbroj nekih dvaju ili više algebarskih razlomaka. Treba odrediti pribrojnike.

Algebarski razlomak $\frac{7 x + 3}{(x - 1) (x + 4)}$ zapišimo u obliku zbroja razlomaka $\frac{A}{x - 1}$ i $\frac{B}{x + 4} .$ Treba odrediti realne brojeve $A$ i $B .$

Složite redoslijed računa.

$\frac{7 x + 3}{(x - 1) (x + 4)} = \frac{A}{x - 1} + \frac{B}{x + 4}$
$\frac{7 x + 3}{(x - 1) (x + 4)} = \frac{2}{x - 1} + \frac{5}{x + 4}$
$7 x + 3 = (A + B) x + 4 A - B$
$A = 2, B = 5$
Razlomci su jednaki, imaju jednake nazivnike pa moraju i brojnici biti jednaki.
$7 x + 3 = A (x + 4)$
$\{\begin{cases} A + B = 7 \\ 4 A - B = 3 \end{cases}$
$\frac{7 x + 3}{(x - 1) (x + 4)} = \frac{A (x + 4) + B (x - 1)}{(x - 1) (x + 4)}$

null

Zatvori

Zapisali smo zadani algebarski razlomak u obliku zbroja jednostavnijih algebarskih razlomaka. Kažemo da smo zadani razlomak rastavili na parcijalne razlomke.

Zadatak 4.

Rastavite zadane algebarske razlomke na parcijalne razlomke.

$\frac{6 x + 14}{(x + 1) (x + 3)} = \frac{A}{x + 1} + \frac{B}{x + 3},$ $A =$ $B =$ .

null

null
$\frac{3 x - 15}{x^{2} - 9} = \frac{A}{x - a} + \frac{B}{x - b},$ $a =$ $b =$
Rastavite nazivnik $x^{2} - 9$ na faktore.

$A =$ $B =$ .

Nekoliko zadataka

Kolekcija zadataka 2

Zadatak 5.

Izračunajte.

${(\frac{3}{2} p - \frac{1}{2} q^{2})}^{2}$
${(a - b)}^{2} + 2 (a - b) (a + b) + {(a + b)}^{2}$
${(5 a + 1)}^{3} - {(5 a - 1)}^{3}$

$\frac{9}{4} p^{2} - \frac{3}{2} p q^{2} + \frac{1}{4} q^{4}$
$4 a^{2}$
$150 a^{2} + 2$

Zadatak 6.

Rastavite na faktore.

$27 x^{3} y^{6} + 8$
$2 x^{3} + 12 x^{2} + 18 x$
$25 x^{2} - 9 {(y - 1)}^{2}$
$10 x^{2} - 15 x y + 2 x - 3 y$

$(3 x y^{2} + 2) (9 x^{2} y^{4} - 6 x y^{2} + 4)$
$2 x {(x + 3)}^{2}$
$(5 x - 3 y + 3) (5 x + 3 y - 3)$
$(2 x - 3 y) (5 x + 1)$

Zadatak 7.

Izračunajte.

$\frac{2 x^{5}}{x^{2} - 8 x + 16} \cdot \frac{x^{2} - 16}{8 x^{3}}$
$\frac{4 x^{2} - 4 x + 1}{20 x^{2} - 5} : \frac{8 x^{3} - 1}{100 x^{2} + 50 x + 25}$

$\frac{x^{2} (x + 4)}{4 (x - 4)}$
$\frac{5}{2 x + 1}$

Zadatak 8.

Izračunajte: $\frac{b}{a^{2} - a b} + \frac{a}{b^{2} + a b} + \frac{1}{a + b} .$

$\frac{a^{2} - a b + b^{2}}{a b (a - b)}$

Zadatak 9.

Izračunajte: $[\frac{3 x + 3}{x - 1} + \frac{x + 1}{x - 1} \cdot \frac{x^{3} - 1}{x^{2} - 1}] : (x + 2) .$ Rezultat možete provjeriti u videozapisu.

Zatvori

Djeljivost

Primjer 1.

Odaberite neki prirodni broj. Zbrojite broj i njegov kvadrat. Rezultat zapišite na ploču. Promotrite i rezultate drugih učenika. Uočavate li pravilnost? Objasnite.

Rezultat je uvijek paran broj. Neka je odabrani broj $n .$ Računali ste: $n^{2} + n = n (n + 1) .$

Dobili smo umnožak dvaju uzastopnih brojeva. Jedan je od njih paran, a drugi je neparan. Umnožak je parnoga i neparnoga broja paran broj.

Kolekcija zadataka 3

Zadatak 10.

Od kvadrata nekoga neparnoga prirodnoga broja oduzmite $1 .$ Zapišite rezultat. Ponovite s nekim drugim neparnim brojem. Uočavate li pravilnost? Objasnite.

Neparni broj veći od $1$ možemo zapisati kao $2 n + 1, n \in N .$ Računamo:

${(2 n + 1)}^{2} - 1 = (2 n + 1 - 1) (2 n + 1 + 1) = (2 n + 2) (2 n) = 4 (n + 1) n .$

Umnožak je djeljiv s $8 .$

Vrijedi li slično svojstvo za razliku kvadrata bilo kojih dvaju prirodnih brojeva?

Zadatak 11.

Odaberite tri uzastopna prirodna broja. Zbrojite njihove kubove. Zapišite rezultat u bilježnicu. Ponovite s neka druga tri uzastopna broja. Uočavate li pravilnost? Objasnite.

Zbroj je djeljiv s $9 .$ Označimo tri uzastopna broja s $n - 1, n, n + 1$ . Računamo:

$\begin{array}{l} {(n - 1)}^{3} + n^{3} + {(n + 1)}^{3} = \\ n^{3} - 3 n^{2} + 3 n - 1 + n^{3} + n^{3} + 3 n^{2} + 3 n + 1 = \\ 3 n^{3} + 6 n = 3 n (n^{2} + 2) \end{array} .$

Zbroj je djeljiv s $3 .$ Treba još dokazati da je izraz $n (n^{2} + 2)$ djeljiv s $3 .$ Postoje tri mogućnosti:

Ako je $n$ djeljiv s $3,$ izraz je djeljiv s $3 .$
Broj $n$ pri dijeljenju s $3$ daje ostatak $1 .$

Tada je $n = 3 k + 1 .$ Treba dokazati da je $n^{2} + 2$ djeljiv s $3 .$ Vrijedi: $n^{2} + 2 = {(3 k + 1)}^{2} + 2 = 9 k^{2} + 6 k + 1 + 2 = 3 (3 k^{2} + 2 k + 1),$ što je djeljivo s $3 .$
Broj $n$ pri dijeljenju s $3$ daje ostatak $2 .$

Tada je $n = 3 k + 2$ pa je $n^{2} + 2 = {(3 k + 2)}^{2} + 2 = 9 k^{2} + 12 k + 4 + 2 = 3 (3 k^{2} + 4 k + 2),$ što je djeljivo s $3 .$

Zatvori

Pascalov trokut

Projekt

U ovom ste modulu naučili formule za kvadrat i kub binoma:

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ i ${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} .$

Koji su koeficijenti u formuli za kvadrat binoma? To su $1,$ $2$ i $1 .$

Koji su koeficijenti u formuli za kub binoma? To su $1,$ $3,$ $3$ i $1 .$

Izračunajte: ${(a + b)}^{4} = (a + b) {(a + b)}^{3} .$ Koji su koeficijenti u toj formuli?

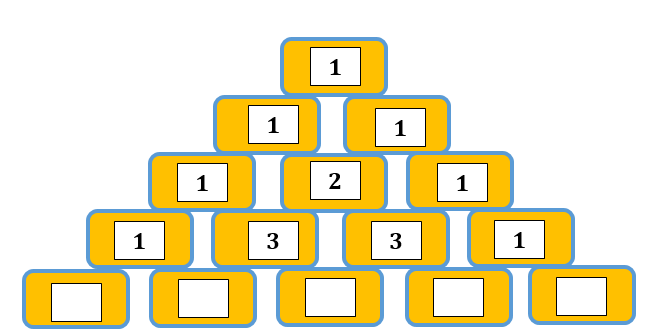
Koeficijente iz tih formula možemo zapisati u obliku trokuta. Nacrtajte takav trokut u bilježnicu pa u posljednji redak upišite koeficijente iz formule za ${(a + b)}^{4} .$

Promotrite neki element u trokutu. Kako ga možemo zapisati s pomoću elemenata iznad njega? Primijenite uočeno pravilo pa napišite idući redak trokuta. Provjerite množenjem jeste li dobili koeficijente u formuli za ${(a + b)}^{5} .$

Pascalov trokut je trokut s brojevima koji na rubnim elementima ima jedinice, a svaki element trokuta dobiven je zbrajanjem elemenata koji su neposredno iznad njega. Brojevi u Pascalovu trokutu koeficijenti su u formulama za potenciju binoma.

Zadatak 12.

Dopišite još nekoliko redova Pascalova trokuta. Promotrite brojeve u Pascalovu trokutu i pronađite pravilnosti. Za prvih nekoliko redaka izračunajte zbroj elemenata u retku. Promotrite brojeve koje ste dobili. Uočavate li pravilnost? Izrecite pravilo. Pročitajte članak o Pascalu i Pascalovu trokutu u časopisu Matka na poveznici.

Zanimljivost

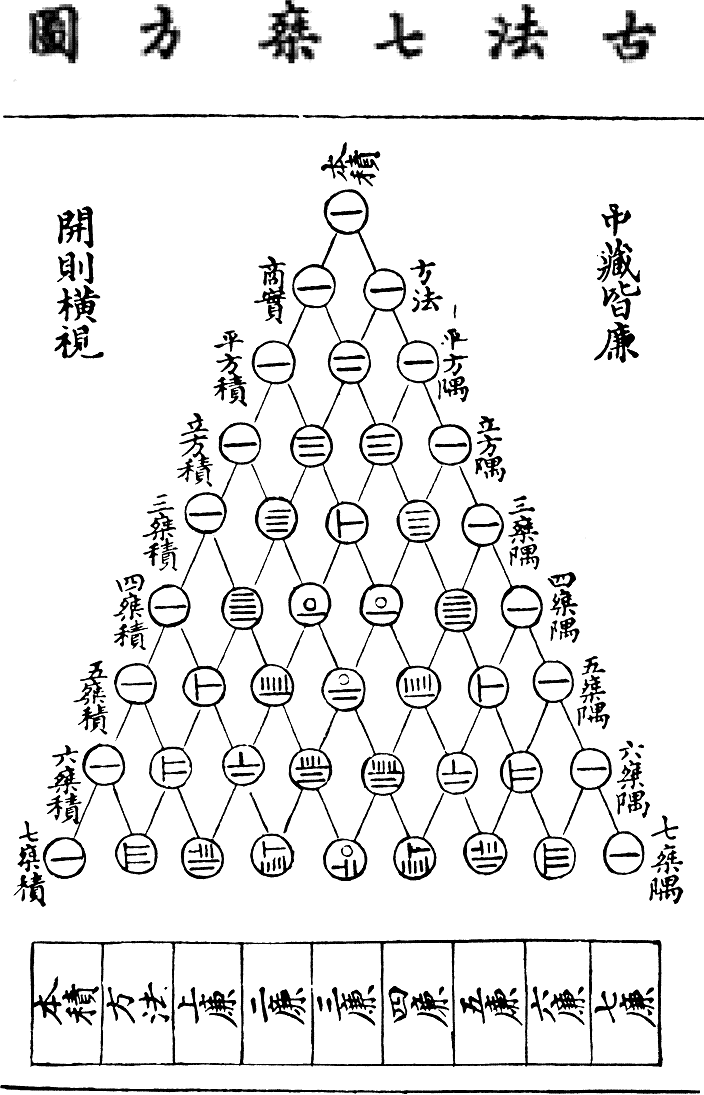
Na slici je ilustracija Pascalovog trokuta iz knjige kineskog matematičara Yanga Huia iz 13. stoljeća. — Yáng Huī (楊輝) (oko 1238. – 1298.), w:en:Image:Yanghui_triangle.gif, Public Domain, Link

Pascalov trokut s koeficijentima potencija binoma naziv je dobio po matematičaru Blaiseu Pascalu, koji ga je opisao u 17. stoljeću, ali trokut je bio poznat mnogim matematičarima prije njega. Sačuvana je ilustracija trokuta iz knjige kineskog matematičara Yanga Huia iz 13. stoljeća.

Kutak za znatiželjne

U ovom ste modulu naučili formule za razliku kvadrata, zbroj i razliku kubova. Vidjeli smo da ne postoji formula za zbroj kvadrata. Ispitajte vrijede li slične formule za zbroj i razliku viših potencija. Zapišite opće formule u bilježnicu. Objasnite ih.

Jeste li uspjeli? Ako niste, izračunajte:

$(a - b) (a^{2} + a b + b^{2})$

$(a - b) (a^{3} + a^{2} b + a b^{2} + b^{3})$

$(a - b) (a^{4} + a^{3} b + a^{2} b^{2} + a b^{3} + b^{4}) .$ Poopćite.
$(a + b) (a^{2} - a b + b^{2})$

$(a + b) (a^{3} - a^{2} b + a b^{2} - b^{3})$

$(a + b) (a^{4} - a^{3} b + a^{2} b^{2} - a b^{3} + b^{4}) .$ Poopćite.

Kolekcija zadataka 4

Zadatak 13.

Uparite formule tako da vrijedi znak jednakosti.

Za svaki neparni broj $n > 1$ vrijedi $a^{n} + b^{n} =$	$(a + b) (a^{n - 1} - a^{n - 2} b + . . . - a b^{n - 2} + b^{n - 1})$
Za svaki prirodni broj $n > 1$ vrijedi $a^{n} - b^{n} =$	$(a - b) (a^{n - 1} + a^{n - 2} b + . . . + a b^{n - 2} + b^{n - 1})$
Za svaki parni prirodni broj $n$ vrijedi $(a + b) (a^{n - 1} - a^{n - 2} b + . . . + a b^{n - 2} - b^{n - 1}) =$	$a^{n} - b^{n}$

null

Zadatak 14.

Pojednostavnite $1 + q + q^{2} + . . . + q^{n} .$

Uvrstimo li u formulu za razliku potencija s eksponentom $n + 1$ umjesto varijable $a$ broj $1,$ a umjesto varijable $b$ varijablu $q,$ dobit ćemo:

$\begin{array}{l} 1 - q^{n + 1} = (1 - q) (1 + q + q^{2} + . . . + q^{n}) \end{array}$ pa je

$\begin{array}{l} 1 + q + q^{2} + . . . + q^{n} = \frac{1 - q^{n + 1}}{1 - q} \end{array} .$

Formula vrijedi za svaki prirodni broj $n$ i svaki realni broj $q \neq 1 .$

Zadatak 15.

Dokažite da je broj:

$5^{2017} + 1$ djeljiv sa $6$
$2^{1985} + 1$ djeljiv s $33 .$

Broj $6$ možemo zapisati kao $6 = 5 + 1,$ a

$5^{2017} + 1 = 5^{2017} + 1^{2017} = (5 + 1) (5^{2016} - 5^{2015} + . . . + 1) = 6 \cdot m, m \in Z .$
Kako možemo dobiti $33$ kao zbroj potencije broja $2$ i broja $1 ?$

$33 = 32 + 1 = 2^{5} + 1,$

$2^{1985} + 1 = {(2^{5})}^{397} + 1 = 32^{397} + 1^{397} = (32 + 1) (32^{396} - 32^{395} + . . . + 1) = 33 \cdot m, m \in Z .$

Zatvori

Na početku...

Zadatak 1.

Parcijalni razlomci

Kolekcija zadataka 1

Zadatak 2.

Zadatak 3.

Zadatak 4.

Nekoliko zadataka

Kolekcija zadataka 2

Zadatak 5.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Zadatak 9.

Djeljivost

Kolekcija zadataka 3

Zadatak 10.

Zadatak 11.

Pascalov trokut

Projekt

Zadatak 12.

Zanimljivost

Kutak za znatiželjne

Kolekcija zadataka 4

Zadatak 13.

Zadatak 14.

Zadatak 15.

...i na kraju