Matematika 1 - 7.4 Primjena sustava linearnih jednadžbi

Na početku...

Učenica na slici kaže: Na ispitu je bilo 30 zadataka. Točno riješen zadatak donosi 4 boda, a za svaki netočno riješen oduzimaju se 2 boda. Učenik kaže: Mislio sam da sam sve zadatke točno riješio. Ali dobio sam samo 66 bodova.

Koliko je zadataka učenik netočno riješio?

Prisjetite se strategije PPRP.
Pročitaj: Što je nepoznato? Označite nepoznate veličine.
Poveži: Pronađite vezu između zadanih i nepoznatih veličina. Postavite jednadžbe.
Riješi: Riješite jednadžbe. Zapišite rješenje sustava jednadžbi.
Provjeri: Jeste li dobili odgovor na postavljeno pitanje? Izvršite radnje koje su još potrebne i provjerite točnost i smislenost rješenja.

Što je u zadatku nepoznato? Nepoznat je broj točno riješenih i broj netočno riješenih zadataka. Označimo broj točno riješenih zadataka s $x$ i broj netočno riješenih zadataka s $y$

Učenik je ukupno rješavao

zadataka. Na točno riješenim zadatcima dobio je

bodova. Na netočno riješenim zadatcima izgubio je

bodova.

$x + y$

$4 x$

$2 y$

null

null
Možemo postaviti jednadžbe: $x + y =$ .
$4 x - 2 y =$ .

null

null
Rješenje sustava jest ( , ).

null

null
Učenik je točno riješio
21
zadatak. Netočno je riješio
9
zadataka.

null

null

Zadatak smo riješili pomoću sustava linearnih jednadžbi s dvjema nepoznanicama. Slični se problemi pojavljuju u mnogim područjima matematike, ostalim predmetima i svakodnevnom životu. Pogledajmo neke primjere.

Numerički problemi ili problemi vezani uz brojeve

Kolekcija zadataka 1

Zadatak 1.

Podijelimo li dva broja, dobit ćemo količnik $4$ i ostatak $16 .$ Koji su to brojevi ako je njihova razlika $103 ?$

Pročitaj: Nepoznata su dva broja. Označimo veći s $x,$ a manji s $y .$
Poveži: Razlika brojeva jest $103 .$ Dijelimo li veći s manjim, količnik je $4,$ a ostatak $16 .$ $x - y = 103,$ $x = 4 y + 16$ .
Riješi: $\{\begin{cases} x = 4 y + 16 \\ (4 y + 16) - y = 103 \end{cases}$ $\{\begin{cases} x = 4 y + 16 \\ 3 y = 87 \end{cases}$ $\{\begin{cases} y = 29 \\ x = 132 \end{cases} .$ Traženi su brojevi $132$ i $29 .$
Provjeri: Razlika brojeva $132$ i $29$ jest $103 .$ Podijelimo $132$ s $29 .$ Količnik je $4,$ a ostatak $16 .$

Dobiveni brojevi zadovoljavaju uvjete zadatka.

Zadatak 2.

Zbroj četiriju brojeva jest $46.2 .$ Poredamo li ta četiri broja od najmanjega do najvećega, možemo uočiti da se povećavaju za isti iznos. Zbroj prvih triju brojeva jest $33.6 .$ Koji su to brojevi?

Označimo najmanji broj s $x,$ a iznos za koji se povećavaju s $y .$

Brojevi poredani od najmanjega do najvećega jesu: $x, x + y, x + 2 y, x + 3 y .$

Zbroj je $46.2$ pa je jedna jednadžba: $x + (x + y) + (x + 2 y) + (x + 3 y) = 46.2 .$

Zbroj prvih triju brojeva jest $33.6$ pa je druga jednadžba: $x + (x + y) + (x + 2 y) = 33.6 .$

Rješavamo sustav:

$\{\begin{cases} 4 x + 6 y = 46.2 \\ 3 x + 3 y = 33.6 \end{cases}$

Rješenje je par $(10.5,0.7) .$

Brojevi su: $10.5,$ $11.2,$ $11.9$ i $12.6 .$

Zadatak 3.

Započnimo niz dvama brojevima. Svaki je sljedeći broj u nizu zbroj prethodnih dvaju. Zbroj prvih

pet tako dobivenih brojeva (uključujući i prva dva) jest

$\frac{55}{6},$ a peti je broj

$\frac{23}{6} .$ Odredite treći broj.

Brojevi su $x,$ $y,$ $x + y,$ $x + 2 y,$ $2 x + 3 y .$

Sustav je $\{\begin{cases} 5 x + 7 y = \frac{55}{6} \\ 2 x + 3 y = \frac{23}{6} \end{cases}$

Rješenje sustava jest $(\frac{2}{3}, \frac{5}{6}) .$

Treći je broj $\frac{3}{2}$

Zadatak 4.

Dodamo li brojniku i nazivniku nekog razlomka broj $12.5,$ dobit ćemo razlomak $\frac{139}{53} .$

Oduzmemo li brojniku i nazivniku tog istog razlomka broj $6.3,$ dobit ćemo razlomak $\frac{507}{77} .$ Koji je to razlomak?

Označimo brojnik razlomka s $x,$ a nazivnik s $y .$ Dobivamo sustav jednadžbi:

$\{\begin{cases} \frac{x + 12.5}{y + 12.5} = \frac{139}{53} \\ \frac{x - 6.3}{y - 6.3} = \frac{507}{77} \end{cases}$

Rješenje sustava jest $(57,14) .$

Razlomak je $\frac{57}{14} .$

Zatvori

Geometrijski problemi

Kolekcija zadataka 2

Zadatak 5.

Krak jednakokračnog trokuta šest je puta duži od osnovice. Izračunajte duljine stranica trokuta ako je njegov opseg $315.9 cm .$

Pročitaj: Označimo duljinu osnovice s $x,$ duljinu kraka s $y .$
Poveži: $\{\begin{cases} y = 6 x \\ x + y + y = 315.9 \end{cases}$
Riješi: Rješenje sustava jest $(24.3,145.8) .$
Provjeri: Duljina osnovice jest $24.3 cm,$ duljina kraka jest $145.8 cm .$

Rješenje je smisleno jer dobiveni brojevi zadovoljavaju nejednakost trokuta.

Zadatak 6.

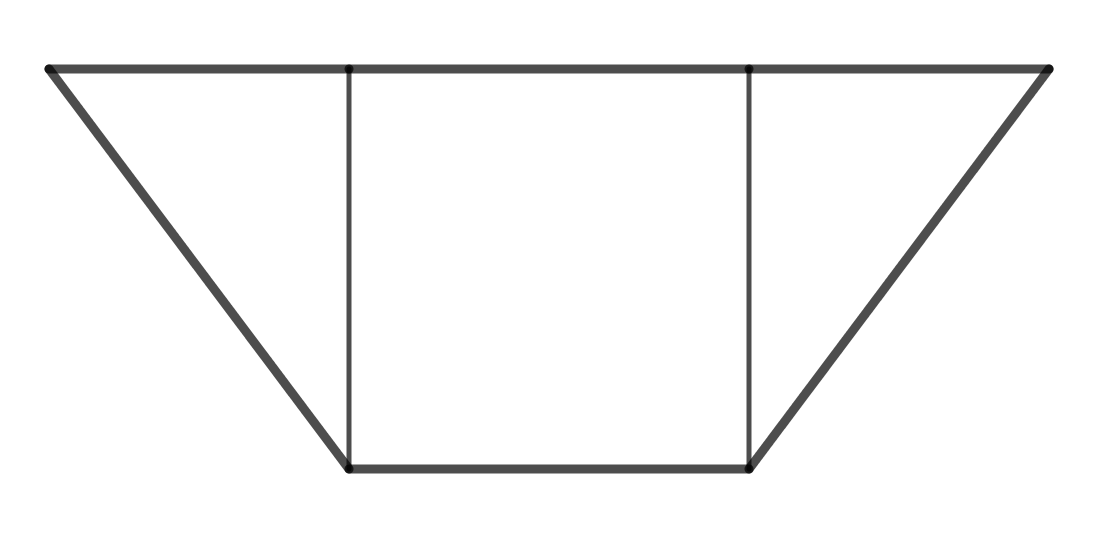
Osnovice jednakokračnog trapeza na slici odnose se kao $2 : 5,$ a zbroj njihovih duljina je $28 cm .$ Četverokut na slici upisan u trapez jest kvadrat. Odredite površinu trapeza.

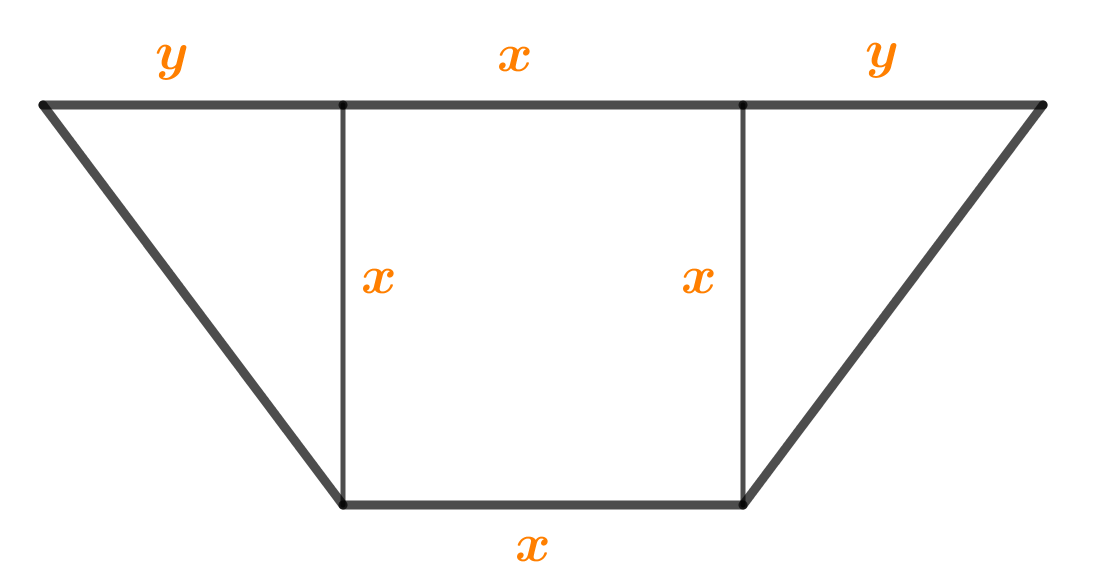
Na slici je jednakokračni trapez na kojemu su označene duljine x i y.

Označimo duljine dužina kao na slici.

Jednadžbe su $\{\begin{cases} x + (x + 2 y) = 28 \\ x : (x + 2 y) = 2 : 5 \end{cases}$

Rješenje je uređeni par $(8,6) .$

Duljine osnovica iznose $20 cm$ i $8 cm .$ Duljina visine jest $8 cm .$

Površina je $x^{2} + x y = 112 {cm}^{2} .$

Zadatak 7.

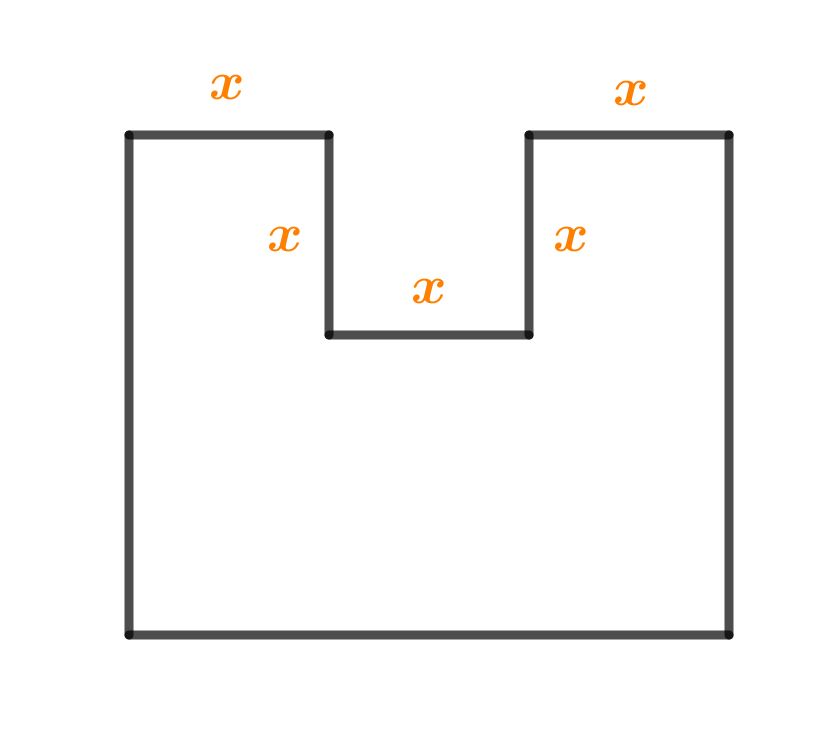
Na slici je pravokutnik iz kojega je izrezan kvadrat.

Razlika duljina stranica pravokutnika jest $9 cm .$ Iz pravokutnika je uz dužu stranicu izrezan kvadrat kao na slici. Odredite površinu tako dobivenog lika ako je njegov opseg $169.6 cm .$

Duljine stranica pravokutnika jesu $3 x$ i $y .$

Sustav jednadžbi jest $\{\begin{cases} 3 x - y = 9 \\ 8 x + 2 y = 169.6 \end{cases} .$

Rješenje sustava jest $(13.4, 31.2) .$

Površina lika jest $3 x y - x^{2} = 1 074.68 {cm}^{2} .$

Zadatak 8.

Povećamo li dužu katetu pravokutnog trokuta za $1 cm$ i skratimo kraću za $3 cm,$ duljina hipotenuze neće se promijeniti. Također se duljina hipotenuze neće promijeniti skratimo li dužu katetu za $4 cm$ i povećamo kraću za $6 cm .$ Odredite duljinu hipotenuze.

Označimo dužu katetu pravokutnog trokuta s $a,$ kraću s $b,$ a hipotenuzu s $c .$

Sustav jednadžbi jest

$\{\begin{cases} {(a + 1)}^{2} + {(b - 3)}^{2} = c^{2} \\ {(a - 4)}^{2} + {(b + 6)}^{2} = c^{2} \end{cases}$

Kvadriramo binome i primijenimo Pitagorin poučak.

Dobivamo sustav:

$\{\begin{cases} a - 3 b = - 5 \\ - 2 a + 3 b = - 13 \end{cases}$

Rješenje sustava jest $(18, \frac{23}{3}) .$

Duljina hipotenuze jest $\frac{\sqrt{3445}}{3} \approx 19.56 cm .$

Zatvori

Cijene

Kolekcija zadataka 4

Zadatak 12.

Anja je na proslavu rođendana donijela $8$ vrećica čipsa od jabuka i $3$ vrećice suhih marelica na koje je potrošila $105.89 kn .$ Matej je u istoj trgovini kupio $5$ vrećica čipsa od jabuka i $7$ vrećica suhih marelica, a platio je $158.38 kn .$ Koja je cijena čipsa, a koja suhih marelica?

Označimo li cijenu vrećice čipsa s $x,$ a cijenu vrećice suhih marelica s $y,$ dobivamo sustav jednadžbi:

$\{\begin{cases} 8 x + 3 y = 105.89 \\ 5 x + 7 y = 158.38 \end{cases}$

Rješenje sustava jest $(6.49, 17.99) .$

Cijena vrećice čipsa jest $6.49 kn,$ a cijena vrećice marelica $17.99 kn .$

Zadatak 13.

Trgovac prodaje sportske torbe po $129.99 kn$ i školske torbe po $139.99 kn .$ Prodao je ukupno $123$ torbe i naplatio $16 468.77 kn .$ Koliko je sportskih, a koliko školskih torbi prodao?

Označimo li broj sportskih torbi s $x,$ a broj školskih s $y,$ dobivamo sustav jednadžbi:

$\{\begin{cases} 129.99 x + 139.99 y = 16 468.77 \\ x + y = 123 \end{cases}$

Rješenje sustava jest $(75,48) .$

Prodano je $75$ sportskih i $48$ školskih torbi.

Zadatak 14.

Petra kupuje vrećice oguljenih badema od $40 g$ po $8.99 kn$ i vrećice pistacija od $30 g$ po $13.99 kn .$ Želi kupiti ukupno $480 g$ badema i pistacija, a na raspolaganju ima $165.86 kn .$ Koliko vrećica badema, a koliko pistacija može kupiti?

Označimo li broj vrećica badema s $x,$ a broj vrećica pistacija s $y,$ dobivamo sustav jednadžbi:

$\{\begin{cases} 8.99 x + 13.99 y = 165.86 \\ 40 x + 30 y = 480 \end{cases}$

Rješenje sustava jest $(6, 8) .$

Petra može kupiti $6$ vrećica badema i $8$ vrećica pistacija.

Zadatak 15.

Anja uspoređuje cijene dviju agencija za iznajmljivanje bicikala. U obje postoji mogućnost unajmljivanja kacige koja se posebno plaća, a cijena unajmljivanja bicikla izražena je u $kn/sat .$ Pronašla je grafove koji prikazuju ovisnost cijene o broju sati najma. Odredite cijenu unajmljivanja kacige u obje agencije te cijenu $1$ sata unajmljivanja bicikla. Za koji bi broj sati unajmljivanja cijena unajmljivanja bila jednaka? Koliko iznosi ta cijena?

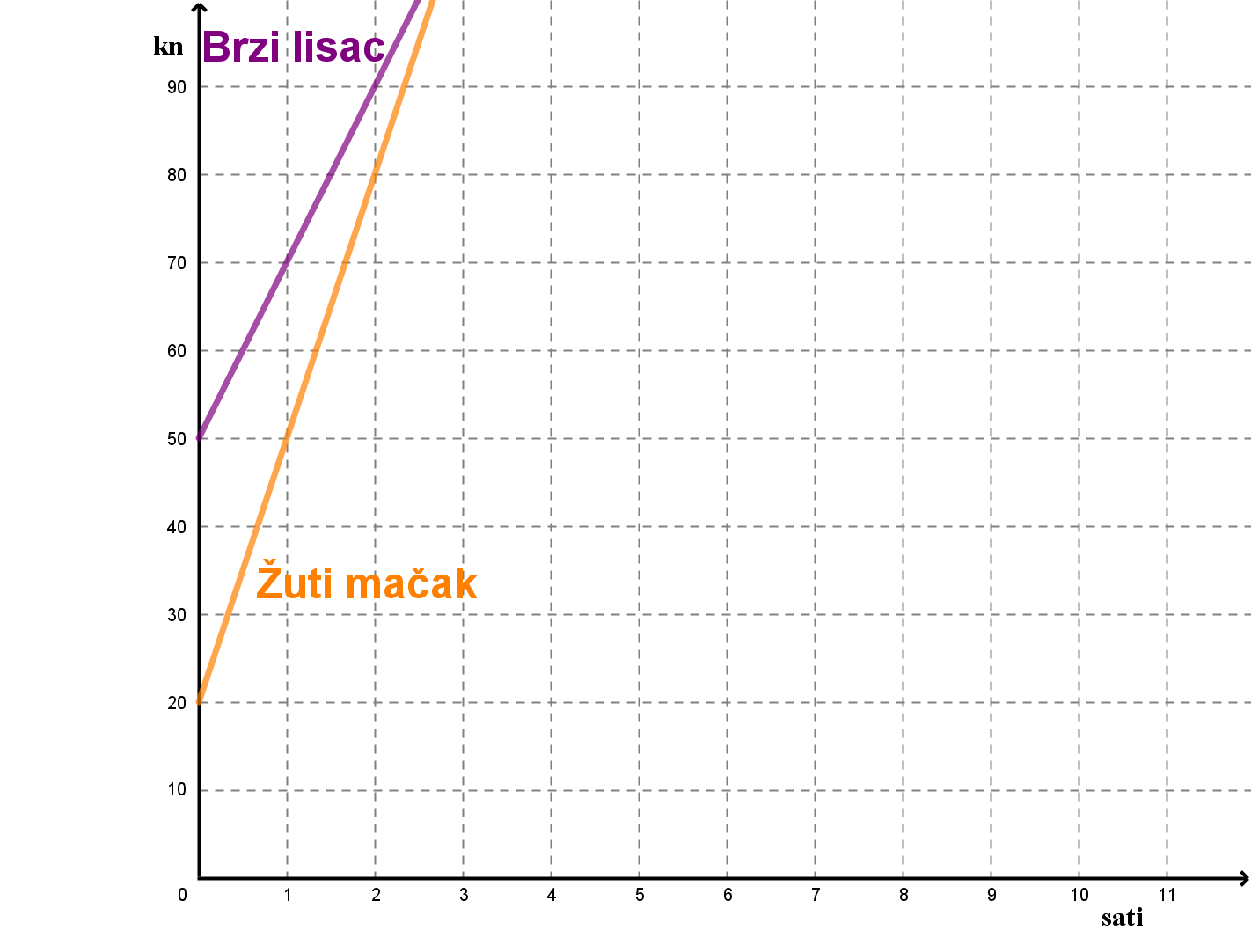
Na slici su grafovi koji prikazuju ovisnost cijene o broju sati iznajmljivanja.

Žuti mačak: za unajmljivanje kacige $20 kn,$ $30 kn$ za $1$ sat unajmljivanja bicikla.

Ovisnost cijene $y$ o broju sati unajmljivanja $x$ jest $y = 30 x + 20 .$

Brzi lisac: za unajmljivanje kacige $50 kn,$ $20 kn$ za $1$ sat unajmljivanja bicikla.

Ovisnost cijene $y$ o broju sati unajmljivanja $x$ jest $y = 20 x + 50 .$

Jednaku ćemo cijenu dobiti rješavanjem sustava

$\{\begin{cases} y = 30 x + 20 \\ y = 20 x + 50 \end{cases}$

Rješenje je $(3, 110) .$

Za tri sata unajmljivanja cijena će biti ista i iznosit će $110 kn .$

Zatvori

Račun smjese

Kolekcija zadataka 5

Zadatak 16.

Čistoća zlata izražava se u karatima i u promilima. Težina zlata mjeri se u uncama.

Karata	Promila
$24$	$999 ‰$
$22$	$916 ‰$
$21$	$875 ‰$
$20$	$833 ‰$
$18$	$750 ‰$
$15$	$625 ‰$
$14$	$585 ‰$

Koliko treba uzeti zlata od $15$ karata, a koliko od $22$ da bi se dobilo $7$ unca $20$ -karatnog zlata?

Označimo li težinu $15$ -karatnog zlata s $x,$ a težinu $22$ -karatnog zlata s $y,$ dobivamo sustav jednadžbi:

$\{\begin{cases} 0.625 x + 0.916 y = 7 \cdot 0.833 \\ x + y = 7 \end{cases}$

Rješenje sustava jest $(\frac{581}{291}, \frac{1456}{291}) .$

Zapišimo rješenja kao decimalne brojeve zaokružene na tri decimale: $x \approx 1.997, y \approx 5.003 .$

Treba uzeti $2$ unce $15$ -karatnog zlata i $5$ unci $20$ -karatnoga.

Zadatak 17.

Od kave po cijeni od $70 kn$ za $1 kg$ i kave po cijeni od $100 kn$ za $1 kg$ treba napraviti mješavinu od $400 kg$ koja će se prodavati po cijeni od $80 kn$ po kilogramu. Koliko kilograma kave svake vrste treba uzeti?

Označimo li masu prve vrste kave s $x,$ a masu druge s $y,$ dobivamo sustav jednadžbi:

$\{\begin{cases} 70 x + 100 y = 400 \cdot 80 \\ x + y = 400 \end{cases}$

Rješenje sustava jest $(\frac{800}{3}, \frac{400}{3})$

Zaokružimo rješenje na cijele brojeve.

Treba uzeti $267 kg$ prve vrste kave i $133 kg$ druge vrste.

Zatvori

Sudari

Povezani sadržaji

U fizici se proučavaju sudari dvaju tijela. Promotrimo centralni elastični sudar. Sudar je centralni ako se središta masa kreću po istom pravcu. Pomoću masa i brzina tijela prije sudara možemo izračunati brzine tijela nakon sudara. Označimo mase tijela s $m_{1}, m_{2},$ brzine prije sudara s $v_{1}, v_{2}$ i brzine nakon sudara s ${\overset{´}{v}}_{1}, {\overset{´}{v}}_{2} .$ Za elastične sudare vrijedi zakon očuvanja energije i zakon očuvanja količine gibanja:

$\begin{array}{l} \{\begin{cases} \frac{1}{2} m_{1} {v_{1}}^{2} + \frac{1}{2} m_{2} {v_{2}}^{2} = \frac{1}{2} m_{1} {\overset{´}{v}}_{1}^{2} + \frac{1}{2} m_{2} {\overset{´}{v}}_{2}^{2} \\ m_{1} v_{1} + m_{2} v_{2} = m_{1} {\overset{´}{v}}_{1} + m_{2} {\overset{´}{v}}_{2} \end{cases} \end{array}$

Dobili smo sustav jednadžbi koji se može zapisati u jednostavnijem obliku (učinite to):

$\{\begin{cases} m_{1} v_{1} + m_{2} v_{2} = m_{1} {\overset{´}{v}}_{1} + m_{2} {\overset{´}{v}}_{2} \\ v_{1} + {\overset{´}{v}}_{1} = v_{2} + {\overset{´}{v}}_{2} \end{cases}$

Pogledajte sljedeću animaciju i riješite zadatak.

Označimo zadane veličine: $m_{1} = 0.03 kg,$ $m_{2} = 0.05 kg,$ $v_{1} = 14 m/s,$ $v_{2} = 0 m/s .$

Postavimo sustav jednadžbi:

$\begin{array}{l} \{\begin{cases} 0.03 \cdot 14 + 0.05 \cdot 0 = 0.03 {\overset{´}{v}}_{1} + 0.05 {\overset{´}{v}}_{2} \\ 14 + {\overset{´}{v}}_{1} = 0 + {\overset{´}{v}}_{2} \end{cases} \end{array}$

Rješenje je $(- 3.5, 10.5) .$

Nakon sudara veća će se kuglica gibati brzinom od $10.5 m/s,$ a manja će se kuglica odbiti u suprotnom smjeru brzinom od $3.5 m/s .$

Kolekcija zadataka 6

Zadatak 18.

Dva tijela čije su mase $1 kg$ i $0.4 kg$ gibaju se po pravcu jedno prema drugom brzinama $5 m/s$ i $- 10 m/s .$ Odredite brzine nakon sudara.

Sustav jednadžbi jest

$\{\begin{cases} {\overset{´}{v}}_{1} + 0.4 {\overset{´}{v}}_{2} = 1 \\ {\overset{´}{v}}_{1} - {\overset{´}{v}}_{2} = - 15 \end{cases}$

Rješenje sustava jest $(- \frac{25}{7}, \frac{80}{7})$

Zapišimo rješenje kao decimalne brojeve zaokružene na dvije decimale.

Prvo se tijelo nakon sudara kreće brzinom $- 3.57 m/s,$ a drugo brzinom $11.43 m/s .$

Zadatak 19.

Kojom brzinom treba kuglica mase $0.2 kg$ udariti u kuglicu mase $0.3 kg$ koja miruje ako želimo da se kuglica koja je mirovala počne gibati brzinom od $4 m/s ?$ Kako će se nakon sudara kretati prva kuglica?

Sustav jednadžbi jest

$\{\begin{cases} 0.2 v_{1} - 0.2 {\overset{´}{v}}_{1} = 1.2 \\ v_{1} + {\overset{´}{v}}_{1} = 4 \end{cases}$

Rješenje sustava jest $(5, - 1) .$

Treba udariti brzinom od $5 m/s .$ Nakon sudara kretat će se u suprotnom smjeru brzinom $1 m/s .$

Zatvori

Kutak za znatiželjne

Kolekcija zadataka 7

Zadatak 20.

Tri prijateljice Maja, Petra i Iva skupljaju knjige iz kriminalističke serije Fearstreet. Kad bi Petra skupila još $6$ knjiga, imala bi ih toliko koliko imaju Maja i Iva zajedno. Kad bi Iva skupila još $10$ knjiga, imala bi ih toliko koliko imaju Maja i Petra zajedno. Njihova su prezimena Anić, Ančić i Aničić. Djevojka Aničić ima $13$ knjiga, a broj knjiga djevojke Anić djeljiv je s $5 .$ Odredite koliko koja djevojka ima knjiga i koje je čije prezime.

Maja Ančić ima $8$ knjiga, Petra Anić ima $15,$ a Iva Aničić $13 .$

Zadatak 21.

Na Županijskom natjecanju iz matematike zadan je zadatak:

Neka je $p, r, s, t \in \{4,8,12,16\} .$ Promatrajući sve moguće izbore brojeva $p, r, s, t$ nađite sva rješenja sustava

$\{\begin{cases} x + y + z = p \\ x + y - z = r \\ x - y + z = s \\ x - y - z = t \end{cases}$

Riješite zadatak.

Zatvori

7.4 Primjena sustava linearnih jednadžbi

Na početku...

Numerički problemi ili problemi vezani uz brojeve

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zadatak 3.

Zadatak 4.

Geometrijski problemi

Kolekcija zadataka 2

Zadatak 5.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Funkcije

Kolekcija zadataka 3

Zadatak 9.

Zadatak 10.

Zadatak 11.

Cijene

Kolekcija zadataka 4

Zadatak 12.

Zadatak 13.

Zadatak 14.

Zadatak 15.

Račun smjese

Kolekcija zadataka 5

Zadatak 16.

Zadatak 17.

Sudari

Povezani sadržaji

Kolekcija zadataka 6

Zadatak 18.

Zadatak 19.

Kutak za znatiželjne

Kolekcija zadataka 7

Zadatak 20.

Zadatak 21.

...i na kraju