

Povežite vektore zadane početnom i završnom točkom s radijvektorom.
|
i
|
|
|
i
|
|
|
i
|
|
|
i
|
|
|
i
|
Pridružite vektore njihovu prikazu u koordinatnoj ravnini.
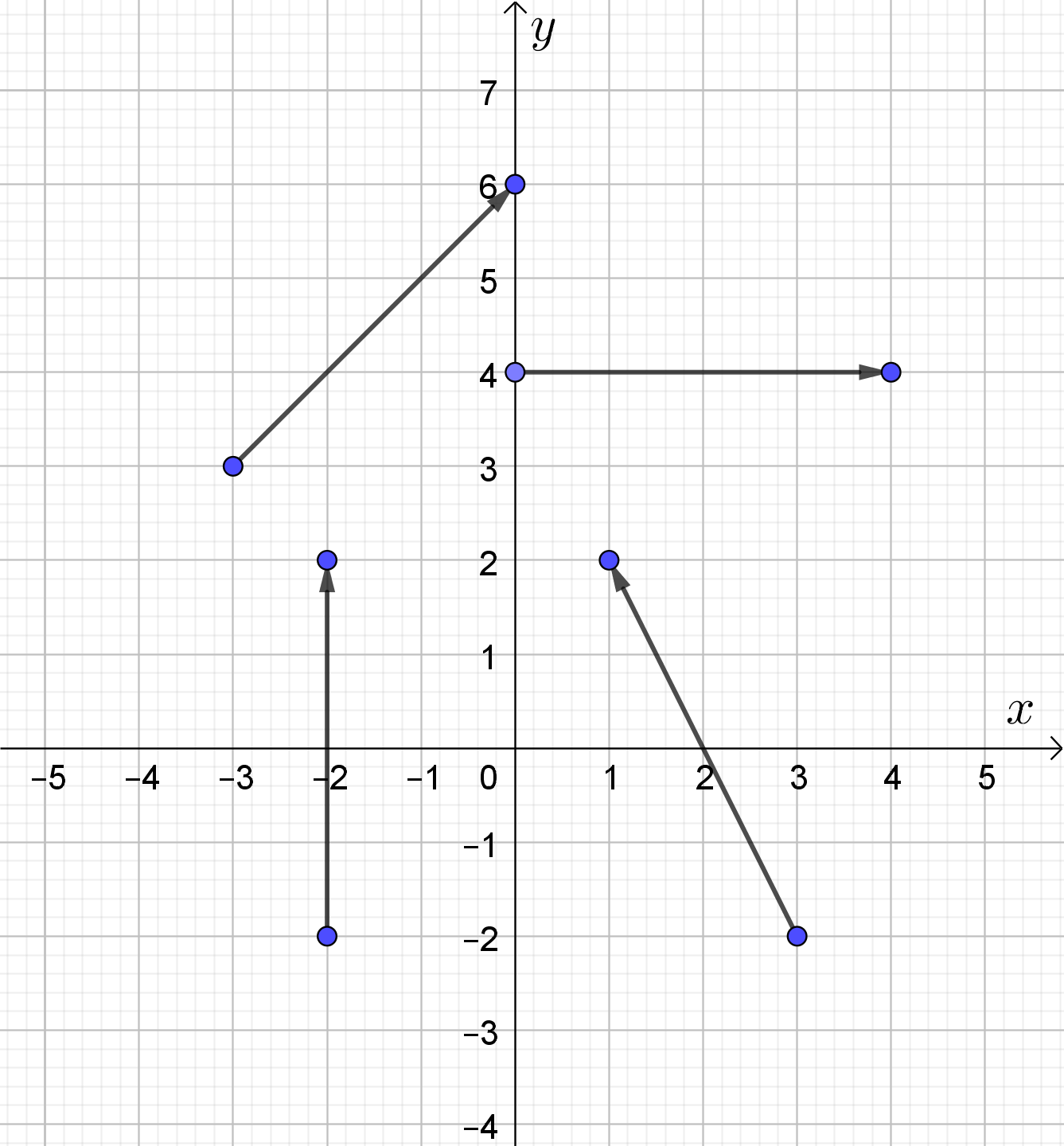
Za vektor kažemo da je
Zadani su vektori:
i
Izračunajte:
Duljina vektora
ako su zadani ovako:
i
jednaka je
Spojite vektore s njihovim skalarnim umnošcima.
|
|
|
|
|
|
|
|
|
|
|
Zadani su vektori:
i
Za kut između vektora vrijedi:
Zadani su vektori:
i
Ako vektor
prikažemo kao linearnu kombinaciju vektora
i
koeficijent
jednak je:
