Matematika 3 - 8.3 Kut između pravaca

Na početku...

Optičke varke često se rade pomoću paralelnih i okomitih pravaca. Pogledaj optičku varku na slici izravno i sa strane. Što uočavaš?

Optička varka

Na slici je poznata optička varka koju je otkrio Ludimar Hermann 1870. godine. Optička varka sastoji se od mreže bijelih paralelnih i okomitih pravaca na crnoj podlozi. Kada je gledaš izravno, neke od točaka na presjecima pravaca postaju crne, a ako gledaš sa strane, sva su sjecišta pravaca bijela.

U sljedećoj optičkoj varci uoči pravce koji su paralelni, koji su okomiti te one koji se sijeku pod nekim drugim kutom. Igrom crne i bijele boje, kao i položajima pravaca, tvoje oči mogu percipirati pravce na sasvim drugi način nego što su oni nacrtani.

Optička varka

Kut dvaju pravaca

Dva pravca $p_{1}$ $p_{1}$ i $p_{2}$ koja se sijeku određuju dva suplementarna kuta. Ako pravci nisu okomiti, dogovorom je određeno da se kutom $α$ između pravaca smatra šiljasti kut koji ti pravci određuju.

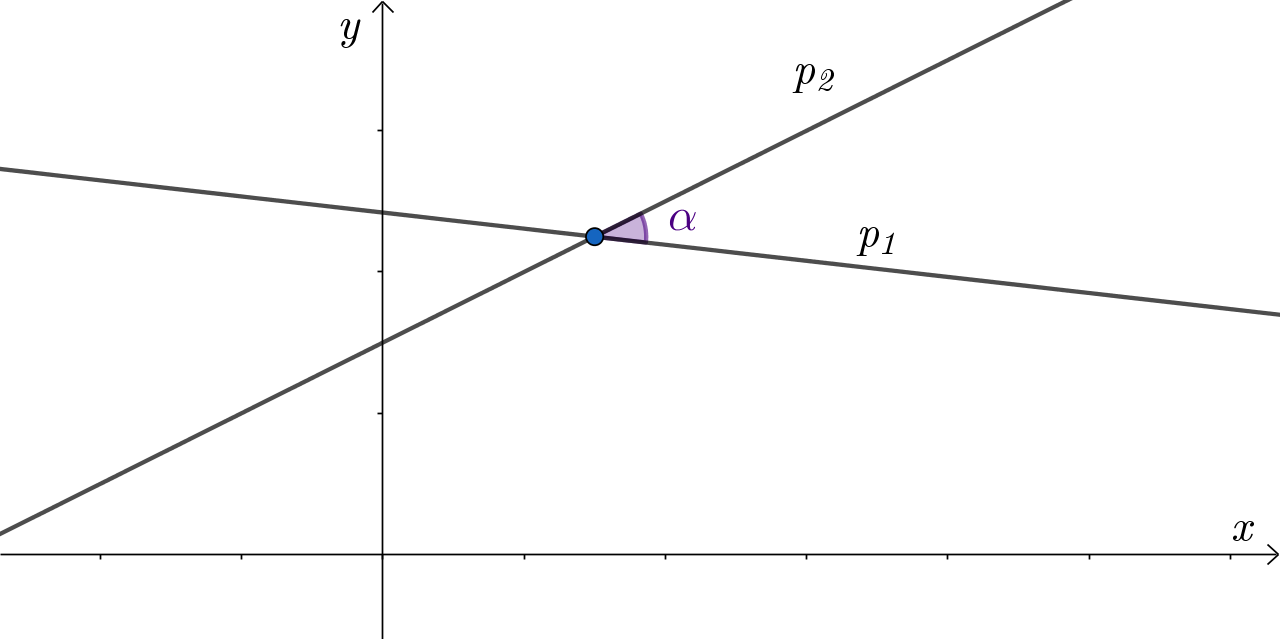
Dva pravca koja se sijeku pod kutem. — Pravci koji se sijeku

Kut između dvaju pravaca jednak je manjem kutu koji ti pravci zatvaraju.

Neka su pravci $p_{1}$ i $p_{2}$ dani eksplicitnim jednadžbama.

$\begin{array}{l} p_{1} . . . y = k_{1} x + l_{1} \\ p_{2} . . . y = k_{2} x + l_{2} \end{array}$

Neka su $α_{1}$ i $α_{2}$ kutovi koje $p_{1}$ i $p_{2}$ zatvaraju s pozitivnim smjerom osi $x .$

Za njihove koeficijente smjera vrijedi: $k_{1} = tg α_{1}$ i $k_{2} = tg α_{2}$

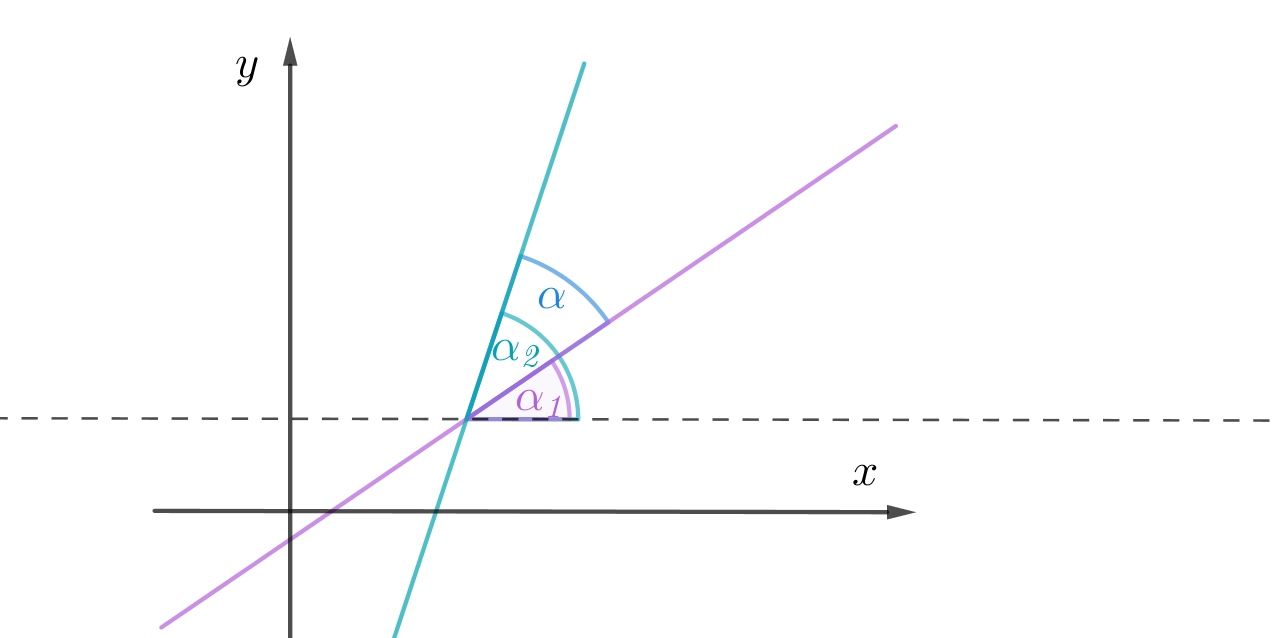
Tehnički crtež kuta između pravaca. — Kut između pravaca

Prema crtežu, šiljasti kut između pravaca $α$ jednak je $α = α_{2} - α_{1}$ .

Vrijedi: $tg α = tg (α_{2} - α_{1}) = \frac{tg α_{2} - tg α_{1}}{1 + tg α_{1} \cdot tg α_{2}} = \frac{k_{2} - k_{1}}{1 + k_{1} \cdot k_{2}} .$

Za kut $α$ između dvaju pravaca $p_{1}$ i $p_{2}$ vrijedi: $tg α = |\frac{k_{2} - k_{1}}{1 + k_{1} k_{2}}| .$

Apsolutna vrijednost u formuli se koristi zato jer kut između pravaca uvijek treba biti šiljasti. Ukoliko je tangens kuta negativan, to ne bi bio slučaj.

Sljedećom interakcijom provjeri kako se promjenom koeficijenata smjera dvaju pravaca mijenja i kut između dvaju pravaca.

Primjer 1.

Pronađi kut između pravaca:

$\begin{array}{l} p_{1} . . . y = 2 x + 5 \\ p_{2} . . . y = 4 x - 3 \end{array} .$

Koeficijenti smjera danih pravaca jesu: $k_{1} = 2$ i $k_{2} = 4 .$

Vrijedi: $tg α = |\frac{4 - 2}{1 + 2 \cdot 4}| = |\frac{2}{1 + 8}| = \frac{2}{9},$ odnosno $α = 12 ° 32' .$

Riješi sljedeće zadatke.

Kolekcija zadataka #1

Pronađi kut između pravaca:

$\begin{array}{l} p_{1} . . . y = - x + 3 \\ p_{2} . . . y = 5 x - 3 \end{array} .$

Koeficijenti smjera danih pravaca jesu $k_{1} = -1$ i $k_{2} = 5 .$

Vrijedi: $tg α = |\frac{5 + 1}{1 - 1 \cdot 5}| = |\frac{6}{1 - 5}| = |- \frac{6}{4}| = \frac{3}{2},$ odnosno $α = 56 ° 18'$ .

Ako su dana dva pravca:

$\begin{array}{l} p_{1} . . . y = 2 x + 1 \\ p_{2} . . . y = 3 x - 2 \end{array} .$

Tada su njihovi koeficijenti smjera:

$k_{1} =$

Razmisli!

$k_{2} =$

Razmisli!

Kut između tih dvaju pravaca jest:

$α =$

Razmisli!

$°$

Razmisli!

$' .$

Pomoć:

Rješenje zapiši u obliku stupnjeva i minuta.

null

Kut između pravaca

$8 x + 4 y + 1 = 0$ i

$x - y + 5 = 0$ je

$α =$

Razmisli!

$°$

Razmisli!

$' .$

Pomoć:

Prisjeti se formule kojom se računa kut između pravaca.

null

Odredi unutarnje kutove trokuta što ga zatvaraju pravci: $y = 0.2 x + 3,$ $y = 2 x$ , $y = - 3 x - 7 .$

Prije rješavanja zadatka skiciraj pravce i uvjeri se kako je trokut koji oni zatvaraju šiljastokutni trokut.

Označimo s $α$ kut između $y = 0.2 x + 3$ i $y = 2 x,$ s $β$ kut između $y = 2 x$ i $y = - 3 x - 7$ i s $γ$ kut između $y = 0.2 x + 3$ i $y = - 3 x - 7 .$

Vrijedi:

$\begin{array}{l} tg α = |\frac{2 - 0.2}{1 + 0.2 \cdot 2}| = |\frac{1.8}{1.4}| = \frac{9}{7} \Rightarrow α = 52 ° 8' \end{array}$

$\begin{array}{l} tg β = |\frac{- 3 - 2}{1 - 2 \cdot 3}| = |\frac{- 5}{- 5}| = 1 \Rightarrow β = 45 ° \end{array}$

$\begin{array}{l} tg γ = |\frac{- 3 - 0.2}{1 - 0.2 \cdot 3}| = |\frac{- 3.2}{0.4}| = 8 \Rightarrow γ = 82 ° 52' \end{array} .$

...i na kraju

Prisjeti se:

Kut između pravaca jednak je kutu za koji treba zarotirati jedan pravac u pozitivnom smjeru da bi se poklopio s drugim pravcem.

Kut

$α$ između dvaju pravaca računa se pomoću formule:

$tg α = |\frac{k_{2} - k_{1}}{1 + k_{1} k_{2}}|$ .

Ako su pravci paralelni, koeficijenti smjera su im jednaki.

Ako su pravci okomiti, koeficijenti smjera su im recipročni i suprotnog predznaka.

8.3 Kut između pravaca

Na početku...

Kut dvaju pravaca

Primjer 1.

Kolekcija zadataka #1

Uvjet paralelnosti i okomitosti pravaca

Zanimljivost

Koeficijenti smjera paralelnih pravaca

Koeficijenti smjera okomitih pravaca

Primjer 2.

Kolekcija zadataka #2

...i na kraju

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: