

U jedinici Opći zakon gravitacije upoznali smo Newtonov zakon gravitacije i gravitacijsku silu.
Područje oko nekog tijela s masom, u kojem na druga tijela koja imaju masu djeluje gravitacijska sila tog tijela, zovemo gravitacijsko polje.
Gravitacijsko polje Zemlje jest radijalno. Strelicama su označene silnice (zamišljene crte) gravitacijskog polja koje svojom gustoćom prikazuju jakost gravitacijskog polja u nekom dijelu prostora.

O čemu ovisi akceleracija sile teže na površini planeta?
Na tijelo mase
koje se nalazi na površini Zemlje djeluje sila teža iznosa
okomito prema središtu Zemlje (Temeljni zakon gibanja – drugi Newtonov zakon).
Sila teža je, zapravo, gravitacijska sila kojom Zemlja privlači sva tijela na površini ili iznad površine. Prema trećem Newtonovu zakonu (treći Newtonov zakon), svako od tih tijela privlači Zemlju silom jednakog iznosa, ali suprotne orijentacije.
Silu težu možemo izraziti s pomoću općeg zakona gravitacije:
pri čemu je
udaljenost tijela na površini Zemlje od njezina središta, tj. polumjer Zemlje.
Uvrštavanjem izraza
u lijevu stranu izraza
dobijemo
te
pri čemu je akceleracija tijela mase u gravitacijskom polju Zemlje, mase na udaljenosti (polumjer Zemlje).
Crna rupa je nebeski objekt koji ima izrazito veliku masu koncetriranu u malom volumenu prostora te je njezino gravitacijsko polje dovoljno jako da, prema Einsteinovoj teoriji, potpuno zakrivi prostorvrijeme oko sebe tako da ništa ne može pobjeći iz dijela prostora omeđenog tzv. horizontom događaja, čak ni svjetlost. Crne rupe ne možemo izravno opažati, a otkrivamo ih po gravitacijskom utjecaju na okolinu.
Iz gornjeg izraza za akceleraciju sile teže uočavamo da
ovisi o udaljenosti tijela od središta Zemlje te možemo jednostavno objasniti zašto je akceleracija sile teže na ekvatoru manja od akceleracije sile teže na polu, s obzirom na to da je Zemlja geoid, tj. spljoštena na polovima, a izbočena na ekvatoru.
Iskoristimo sljedeću interakciju i pogledajmo kako težina tijela ovisi o položaju na Zemlji.
Primjer 1.
Koristeći se iznosom akceleracije sile teže na površini Zemlje i primjenjujući opći zakon gravitacije, izračunajte masu Zemlje.
Iz
dobijemo izraz
u koji uvrstimo vrijednosti za:
polumjer Zemlje
gravitacijsku konstantu
i
Ako se tijelo nalazi na visini iznad površine Zemlje, ovisnost akceleracije sile teže o visini možemo matematički predočiti izrazom
odnosno
Primjer 2.
Međunarodna svemirska postaja (ISS) giba se na visini od iznad površine Zemlje. Izračunajte
Iznos gravitacijskog polja na površini Zemlje polumjera jest Koliko iznosi gravitacijsko polje na udaljenosti od 10 Zemljinih polumjera od središta Zemlje?
Tijelo mase
koje miruje na površini nebeskog tijela ima težinu
pri čemu je jakost gravitacijskog polja na mjestu na kojem se tijelo nalazi.
Na površini nebeskog tijela mase
i polumjera
vrijedi
Napomena: ovaj se izraz dobiva na sličan način kao izraz za
na Zemlji.
S pomoću sljedeće interakcije istražite i usporedite težinu tijela na Zemlji, Mjesecu i Marsu.
Satelit je nebesko tijelo koje se giba u orbiti oko planeta, zvijezde ili nekog drugog masivnog tijela. Prirodne satelite nazivamo još i mjesecima, pratiocima ili trabantima. Primjeri prirodnih satelita jesu Mjesec, planeti i kometi.
Umjetni sateliti napravljeni su i lansirani u orbitu Zemlje ili nekog drugog planeta radi različitih namjena, komunikacije, navigacije, prognoziranja vremena, znanstvenih istraživanja i drugih potreba.
Satelitom se smatra i Međunarodna svemirska postaja (ISS), kao i svemirske letjelice s ljudskom posadom ako su u orbiti.
Orbite satelita razlikuju se ovisno o namjeni i klasificiraju se na različite načine. Poznate su ove vrste orbita: niska Zemljina orbita, polarna orbita i geostacionarna orbita.
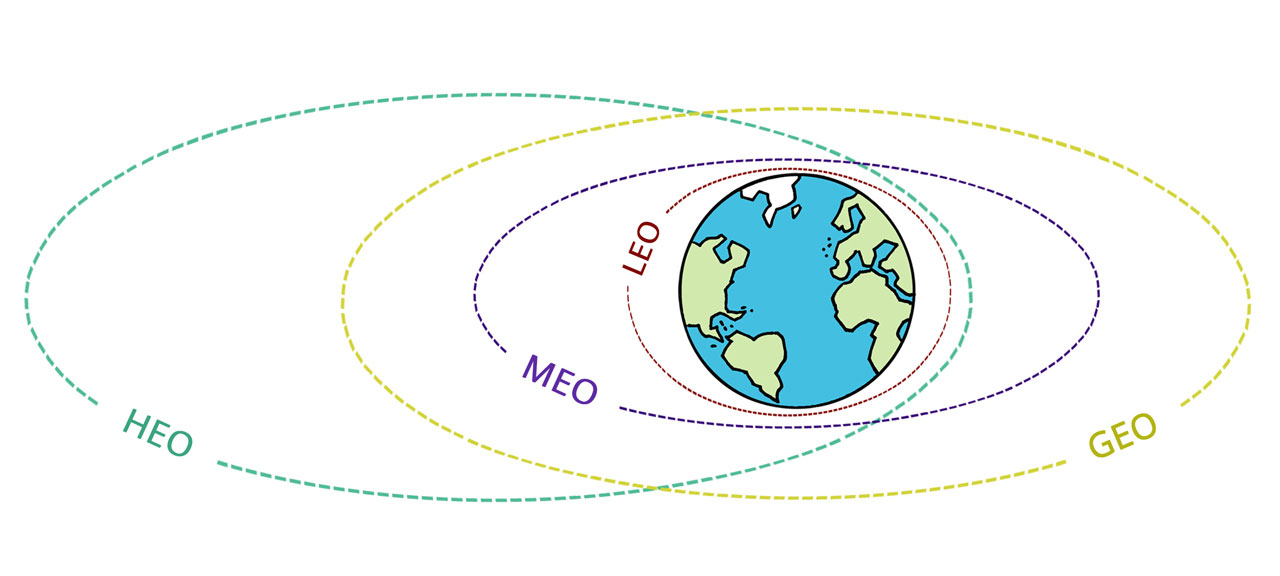
Napomena:
Dakle, ako tijelo koje se izbaci s površine Zemlje ostane u Zemljinoj orbiti, ono postaje njezin umjetni satelit.
Ako za orbitu pretpostavimo kružnicu, na satelit koji se giba na određenoj visini stalno djeluje centripetalna sila koja ga vuče prema središtu u smjeru polumjera kruženja. O tome smo govorili u jedinici Jednoliko gibanje po kružnici.
U ovom je primjeru centripetalna sila koja djeluje na satelit gravitacijska sila pa vrijedi:
pri čemu je:
Ako navedenu jednakost pomnožimo sa sljedećim:
dobijemo:
odnosno
Iz izraza vidimo da brzina kojom se satelit giba po kružnoj orbiti ne ovisi o masi satelita, već samo o udaljenosti od površine Zemlje, tj. visine na kojoj se giba. Brzina satelita smanjuje se s povećanjem udaljenosti od središta Zemlje do satelita, tj. s povećanjem visine.
Primjer 3.
Srednja udaljenost između Mjeseca i Zemlje iznosi . Kolika je brzina i period Mjeseca u njegovu gibanju oko Zemlje? Masa Zemlje iznosi
Poznati su nam podatci:
Za gibanje Mjeseca po njegovoj orbiti oko Zemlje odgovorna je centripetalna sila:
Gravitacijska sila kojom Zemlja privlači Mjesec dana je izrazom:
Navedene izraze možemo izjednačiti jer gravitacijska sila djeluje kao centripetalna sila:
te dobijemo
Brzina kojom se Mjesec giba približno iznosi
Poznat nam je izraz za brzinu:
Ako uzmemo da je orbita Mjeseca kružnica, prijeđeni put jednak je opsegu kružnice:
te uvrštavanjem dobijemo:
odakle je period rotacije (ophod) T:
Uvrštavanjem dobijemo:
Pogledajmo još jedanput animaciju u kojoj je prikazano gibanje geostacionarnog satelita oko Zemlje i prisjetimo se da je centripetalna sila gravitacijska sila između satelita i Zemlje. Obratite pozornost na smjer i orijentaciju obodne brzine, centripetalne sile i centripetalne akceleracije.
Uz pretpostavku da se tijelo giba neposredno iznad površine Zemlje, uvjet kruženja satelita može se pojednostavniti te vrijedi:
odakle dobijemo brzinu kojom se treba satelit izbaciti da bi jednoliko kružio u blizini površine Zemlje.
Tu brzinu zovemo prva kozmička brzina.
Prva kozmička brzina jest najmanja brzina kojom treba izbaciti tijelo sa Zemlje da bi ostalo u Zemljinoj orbiti.
Izbacuje li se satelit manjom brzinom od prve kozmičke brzine, neće biti zadovoljen uvjet kruženja (jednakost centripetalne i gravitacijske sile) jer će gravitacijska sila biti veća od potrebne centripetalne te će se satelit vratiti na Zemlju.
Tijelo mase na površini planeta mase i polumjera ima gravitacijsku potencijalnu energiju u odnosu na središte planeta (Gravitacijska potencijalna energija) čiji je iznos:
Da bi tijelo napustilo planet, treba dobiti brzinu takvu da kinetička energija tijela
bude veća od gravitacijske potencijalne energije.
Ako izjednačimo gravitacijsku potencijalnu i kinetičku energiju
i pomnožimo s
dobijemo:
odnosno
pri čemu je brzina oslobađanja ili druga kozmička brzina.
Druga kozmička brzina povezana je s prvom sljedećim izrazom:
Za Zemlju ta brzina iznosi
Druga kozmička brzina jest najmanja brzina koju treba imati neko tijelo izbačeno blizu površine planeta da bi napustilo gravitacijsko polje planeta.
Drugom kozmičkom brzinom sa Zemlje se lansiraju svemirske letjelice (međuplanetarne sonde) na putu k Mjesecu i planetima Sunčeva sustava.
Ponovimo o kozmičkim brzinama uz animaciju koja prikazuje zamišljeni Newtonov pokus ispaljivanja topovske kugle.
Učili ste iz Geografije u osnovnoj školi o periodičnim pojavama plime i oseke na Zemlji, a na Biologiji ste spominjali njihov utjecaj na žive organizme.
Plima i oseka pojavljuju se zbog gravitacijskog djelovanja Mjeseca i Sunca na Zemlju te zbog vrtnje (rotacije) Zemlje. Plima je dizanje, a oseka opadanje razine mora i oceana. Plima se javlja istovremeno na suprotnim dijelovima Zemlje. Zbog Zemljine rotacije područja plime i oseke izmjenjuju se svakih
sati.
Na slici vidimo istodobno djelovanje Mjeseca i Sunca na morske mijene i to: za vrijeme mladog i punog Mjeseca, tzv. sizigija, kada se Sunčevo i Mjesečevo plimno djelovanje zbrajaju, te za vrijeme prve i posljednje četvrti (kvadrature), kada je ukupno djelovanje Mjeseca i Sunca najslabije.
Prikaz morskih mijena s obzirom na položaj Mjeseca i Sunca
Na slici vidimo da je utjecaj na plimu i oseku najjači u vrijeme mladog i punog Mjeseca jer je njegov utjecaj pojačan utjecajem položaja Sunca s obzirom na Zemlju. Naime, Sunce, Zemlja i Mjesec tada se nalaze u ravnini te je zbog toga utjecaj na plimu i oseku najjači.
Napomena: Koliko će plima i oseka biti jake ovisi također i o promjeni udaljenosti između Mjeseca i Zemlje. Plima i oseka jačaju kada se Mjesec nalazi u perigeju, a slabe kada je u apogeju.
Najveći su rasponi morskih mijena: u Kanadi (Fundy Bay) metara, u Engleskoj (Severn) metara i u Francuskoj (Granville u Donjoj Normandiji) metara. U Jadranskome moru ti su rasponi od (jug) do metar (sjever).
Razmislite zbog čega su morske mijene zbog djelovanja Mjeseca oko puta veće od mijena zbog djelovanja Sunca. Što je uzrok pojavi morskih mijena?
Mjesečeve morske mijene veće su od Sunčevih zbog toga što je gravitacijska sila proporcionalna masi tijela, a obrnuto proporcionalna kvadratu udaljenosti između tijela.
Govorili smo o gravitacijskom polju te odredili ubrzanje slobodnog pada u gravitacijskom polju planeta. Također smo opisali osnovna svojstva gibanja satelita i planeta te protumačili izraz za prvu i drugu kozmičku brzinu. Provjerite svoje znanje kako biste vidjeli koliko ste razumjeli.
Na kojoj je udaljenosti od površine planeta sila kojom planet privlači neko tijelo
puta manja od sile kojom ga privlači kada je na njegovoj površini? Zaokružite rezultat.
Vrijeme potrebno za obilazak planeta oko Sunca ovisi o njegovoj udaljenosti od Sunca. Pri većim udaljenostima obilazak traje dulje.
Gravitacijsko ubrzanje na Sjevernom polu veće je nego na ekvatoru zbog Zemljine spljoštenosti.