Fizika 2 - 2.8 Carnotov kružni proces

Na početku...

Nicolas Léonard Sadi Carnot (Pariz, 1. lipnja 1796. - Pariz, 24. kolovoza 1832)

Godine 1824. Sadi Carnot analizirao je toplinski stroj koji bi imao najveću moguću djelotvornost pri radu između dvaju spremnika topline. Dokazao je da se djelotvornost takvog stroja može izračunati poznavanjem temperatura toplijeg i hladnijeg spremnika. Stroj koristi idealan plin kao radni fluid. Analizirat ćemo i detaljno opisati Carnotov ciklus ili Carnotov kružni proces, koji se sastoji od četiriju reverzibilnih procesa.

Carnotov ciklus jest teorija koju je Carnot iznio javnosti 1824. godine. Glavna je ideja teorije da svaki toplinski stroj prima toplinsku energiju iz spremnika više temperature, samo dio te energije pretvara u rad, a ostatak toplinske energije bezuvjetno predaje spremniku niže temperature. U teoriji se navodi i činjenica da se ukupna toplinska energija iz spremnika topline više temperature ne može sva pretvoriti u rad. Carnot je definirao idealni toplinski stroj s najvećim faktorom korisnosti, kojemu rad ovisi samo o temperaturnoj razlici dvaju spremnika topline, bez obzira na vrstu plina koja u stroju obavlja rad.

Što se događa u pojedinim fazama Carnotova kružnog procesa detaljno ćemo analizirati na primjeru idealnog plina zatvorenog u cilindru s pokretnim klipom.

Carnotov kružni proces

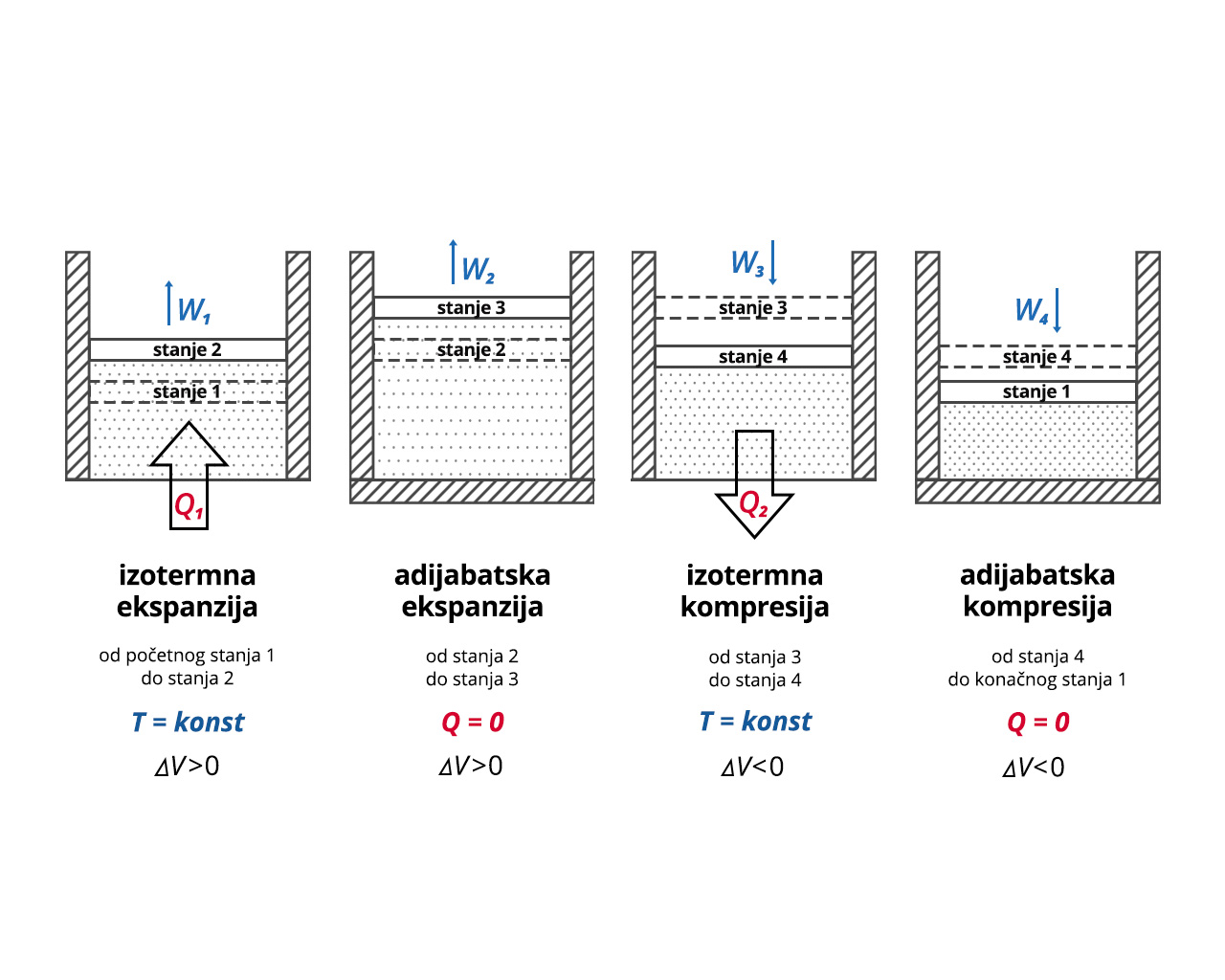
Prikaz Carnotovog kružnog procesa — Carnotov kružni proces

Pogledajte pažljivo animirani prikaz faza Carnotova kružnog procesa u $p, V$ dijagramu.

Analiza Carnotova kružnog procesa po fazama

$1 \to 2$ izotermna ekspanzija – toplina $Q_{1}$ dovodi se plinu iz toplijeg spremnika pri stalnoj temperaturi $T_{1} .$ Nema promjene unutarnje energije plina, $Δ U = 0 .$ Plin u cilindru obavlja rad koji je jednak dovedenoj toplini, zbog čega se klip podiže, a volumen plina povećava.

$2 \to 3$ adijabatska ekspanzija – plin je termički izoliran pa nema izmjene topline s okolinom, odnosno $Q = 0 .$ Plin obavlja rad na račun smanjenja unutarnje energije pa se temperatura plina smanjuje na vrijednost $T_{2} .$ Klip se i dalje podiže, a volumen povećava.

$3 \to 4$ izotermna kompresija – toplina $Q_{2}$ prenosi se hladnijem spremniku pri stalnoj temperaturi $T_{2} .$ Nema promjene unutarnje energije plina, odnosno $Δ U = 0 .$ Na plinu se obavlja rad koji je prema prvom zakonu termodinamike jednak otpuštenoj toplini $Q_{2} .$ Zbog obavljanja toga rada, klip se spušta, a volumen se plina u cilindru smanjuje.

$4 \to 1$ adijabatska kompresija – nema izmjene topline s okolinom, a rad koji se obavlja nad plinom događa se na račun povećanja unutarnje energije plina. Pritom plinu raste temperatura na vrijednost $T_{1} .$ Plin se vraća na početne vrijednosti tlaka i volumena i time se ciklus završava.

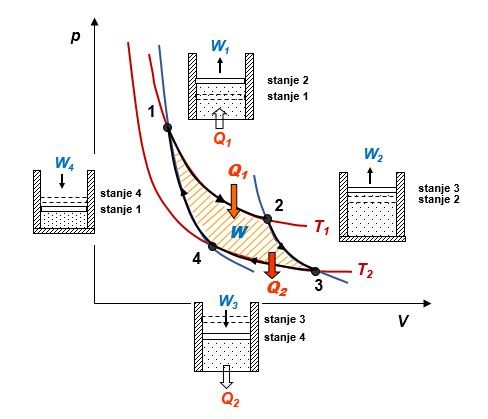
Faze Carnotovog kružnog procesa prikazane u pV dijagramu — Faze Carnotova kružnog procesa prikazane u p, V dijagramu

Rad i korisnost Carnotova ciklusa

Primjenom prvog zakona termodinamike za Carnotov ciklus dobijemo rad: $W = Q_{1} - Q_{2} .$

Površina omeđena zatvorenim krivuljama u $p, V$ dijagramu predstavlja rad dobiven izvođenjem jednog ciklusa u Carnotovom kružnom procesu. Toplina $Q_{1}$ toplina je koju radni medij, odnosno plin prima iz toplijeg spremnika, a $Q_{2}$ je toplina koju plin predaje hladnijem spremniku. Na temelju svojih proučavanja, Carnot je pokazao da vrijedi:

$\frac{Q_{2}}{Q_{1}} = \frac{T_{2}}{T_{1}} .$

U jedinici 2.7. Toplinski stroj definirali smo korisnost toplinskog stroja i izveli formulu po kojoj se korisnost može izračunati.

$η = 1 - \frac{Q_{2}}{Q_{1}}$

Uz zaključke Carnotovih istraživanja prema kojima je $\frac{Q_{2}}{Q_{1}} = \frac{T_{2}}{T_{1}},$ može se napisati formula za korisnost Carnotova kružnog procesa.

Korisnost Carnotova kružnog procesa definirana je formulom:

$η = 1 - \frac{T_{2}}{T_{1}}$

pri čemu je $T_{1}$ temperatura toplijeg, a $T_{2}$ temperatura hladnijeg spremnika.

Temperatura toplijeg spremnika idealnog toplinskog stroja koji obavlja Carnotov kružni proces iznosi $400 ° C,$ a temperatura hladnijeg spremnika $20 ° C$ . Kolika je korisnost ovog stroja?

$95 %$
U formulu ste uvrstili Celzijeve stupnjeve. Velikim slovom $T$ u fizici se označava termodinamička temperatura koja se iskazuje u kelvinima.

$1$
Ne postoji toplinski stroj koji ima korisnost $1$

$2$
Ne postoji toplinski stroj koji ima ovoliku korisnost

$0,56$
Bravo! Ovo je točan odgovor.

Pomoć:

U jednadžbu za korisnost stroja koji radi po Carnotovom kružnom procesu uvrstite temperaturu izraženu u kelvinima.
Temperatura toplijeg spremnika idealnog toplinskog stroja koji obavlja Carnotov kružni proces iznosi $400 ° C,$ a temperatura hladnijeg spremnika $20 ° C .$ Odredite rad koji može dati stroj ako od grijača primi količinu topline od $400 kJ .$

$225,8 kJ$
Bravo! Ovo je točan rezultat.

$224 W$
Iskazuje li se rad u vatima, $W ?$

$225,8 J$
Paziti na mjerne jedinice!

Nema rada u ovom ciklusu
Ipak ima rada. Provjerite još jednom.

Pomoć:

Za rješavanje ovog zadatka možete koristiti podatke iz prethodnog zadatka.

Postupak:

O korisnosti stroja raspravljali smo u jedinici 2.7. Toplinski stroj. Ondje je napisana formula kojom se može izračunati korisnost stroja:

$η = \frac{W}{Q_{1}} .$

Iz te formule slijedi:

$W = η Q_{1} = 224 kJ .$

Proučite Carnotov kružni proces prikazan u $p, V$ dijagramu i pravilno spojite parove za svaki dio tog procesa.

p, V dijagram Carnotovog kružnog procesa

Izotermna ekspanzija
Adijabatska ekspanzija
Izotermna kompresija
Adijabatska kompresija

Kutak za znatiželjne

Ledomat treba $30$ litara vode temperature $0 ° C$ pretvoriti u led temperature $0 ° C$ . Temperatura okoline je $30 ° C .$ Koliki rad mora obaviti ledomat kako bi vodu pretvorio u led ako radi po obrnutom Carnotovu kružnom procesu? Latentna toplina taljenja ovog leda iznosi $335 000 J/kg .$

Ledomat mora obaviti rad od $1 104 395,6 J$ kako bi vodu pretvorio u led.

2.8 Carnotov kružni proces

Na početku...

Carnotov kružni proces

Rad i korisnost Carnotova ciklusa

Kutak za znatiželjne

...i na kraju

2.9 Drugi zakon termodinamike