

Jakost električnog polja možemo odrediti s pomoću Coulombova zakona, kao što smo i pokazali u prethodnoj jedinici, ali i s pomoću tzv. Gaussovog zakona, kojim se može odrediti jakost električnog polja u slučaju simetričnih raspodjela naboja.
Gaussov zakon proizlazi iz Coulombova zakona.
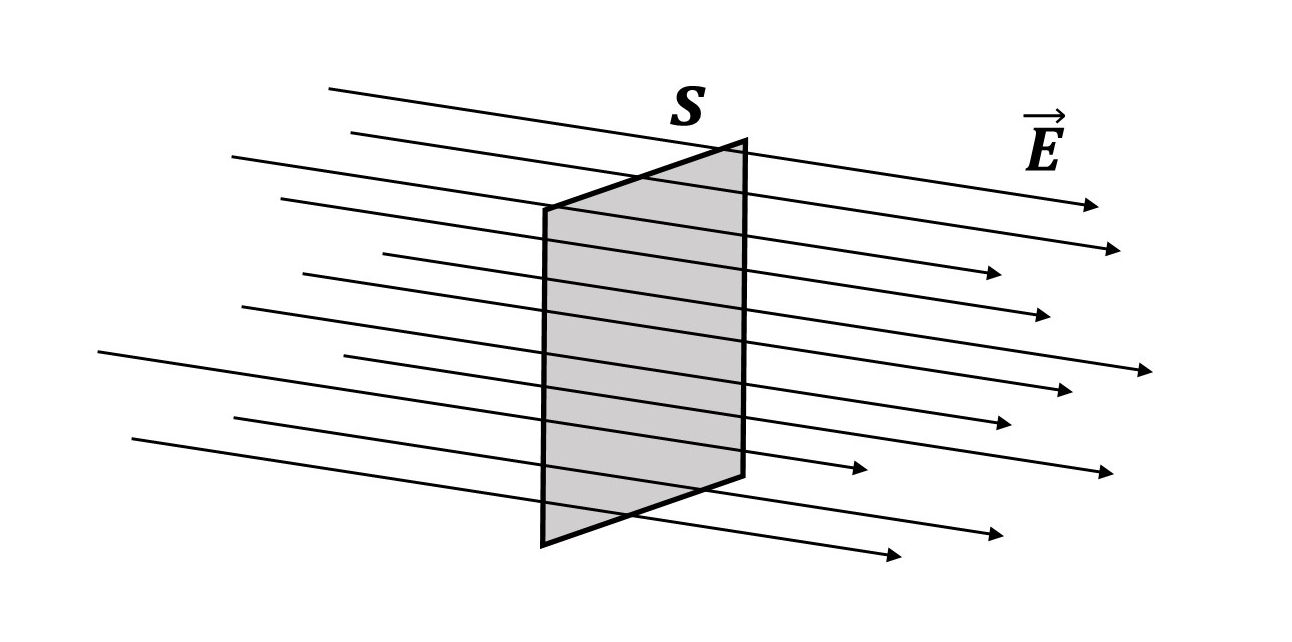
Tok električnog polja je skup električnih silnica koje prolaze nekom plohom.
Tok homogenog električnog polja kroz ravnu plohu ploštine
koja je okomita na silnice električnog polja
određen je umnoškom iznosa jakosti električnog polja
i iznosa
vektora površine
Tok električnog polja je skalarna veličina. Mjerna jedinica za električni tok je
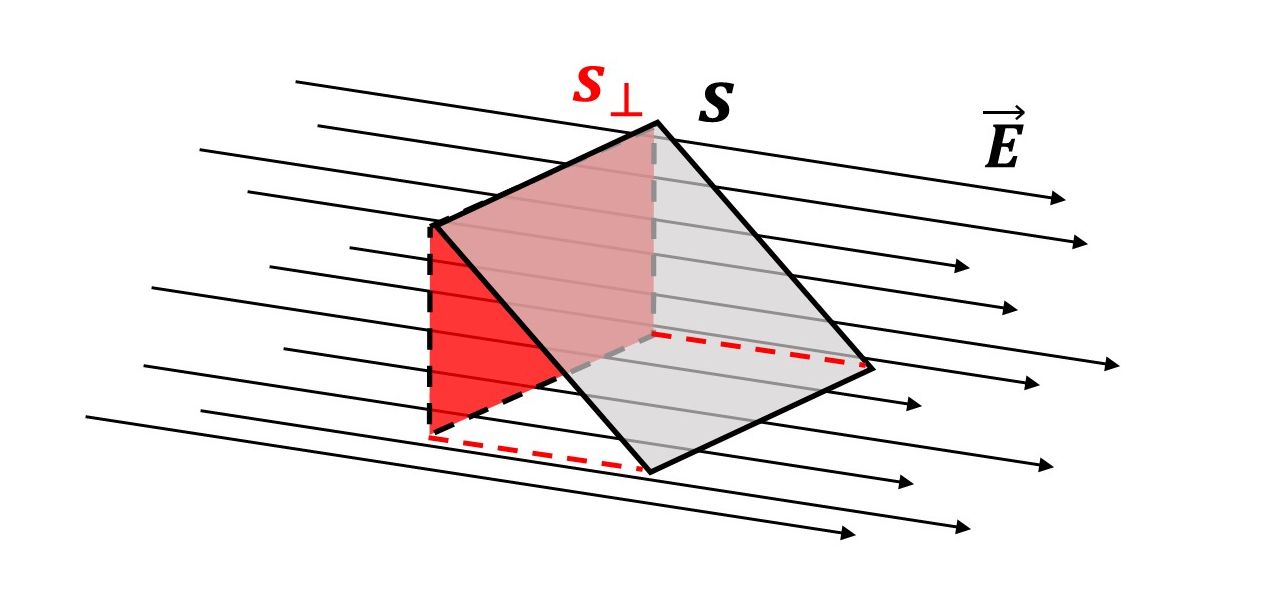
Ako silnice upadaju na plohu pod nekim kutom , tada je tok jednak umnošku jakosti električnog polja i projekcije površine na koju silnice upadaju okomito
tj.
Kut
je kut između vektora jakosti električnog polja
i vektora površine
koji je okomit na plohu, a iznosi ploštinu te plohe.
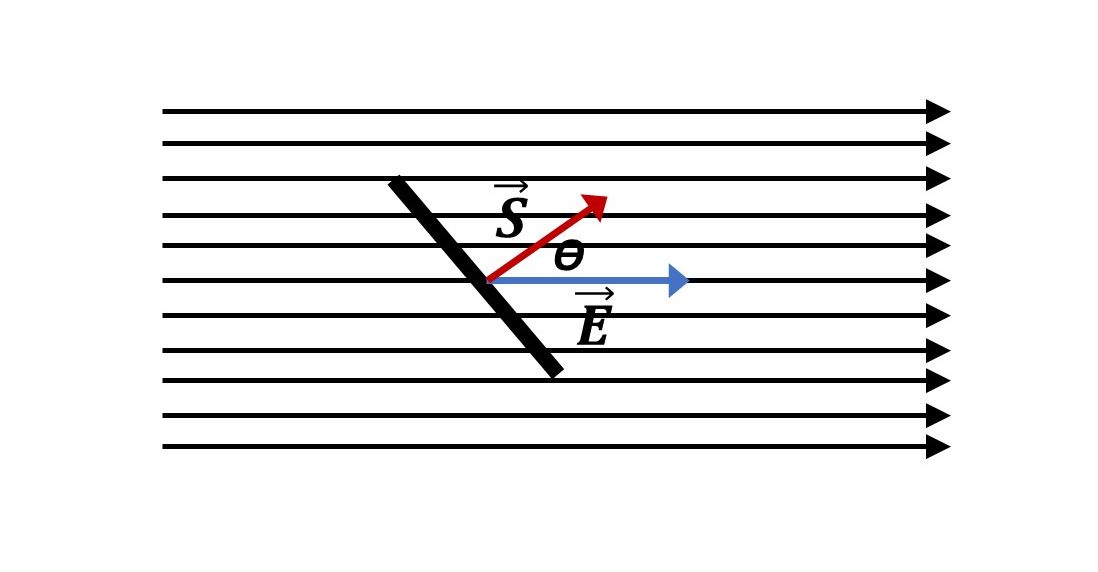
U animaciji je bočni prikaz rotacije plohe površine
u homogenom električnom polju. Električni tok je najveći kad je kut
stupnjeva.
Kroz plohu ne prolazi nijedna silnica pri kutu
od stupnjeva.
Odredite električni tok kroz sferu polumjera u čijem središtu se nalazi točkasti naboj od

Johann Carl Friedrich Gauß (Braunschweig, 30. travnja 1777. - Göttingen, 23. veljače 1855.), njemački matematičar i astronom. Svestrani matematički genij i jedan od najvećih matematičara uopće. Postavio je osnove teorije brojeva, istraživao zakrivljene plohe, proučavao magnetska i električna polja. Otkrio je Bodeov zakon proporcija, pridonio binarnom teoremu, zakonu kvadrata recipročnosti... Najvažnija statistička raspodjela nazvana je po njemu - Gaussova krivulja, a rijetko je koje područje matematike, fizike i astronomije ostavio netaknutim.
Gaussov zakon iskazuje vezu između ukupnog toka električnog polja kroz proizvoljnu zatvorenu plohu (tzv. Gaussova ploha) i naboja zatvorenog unutar plohe.
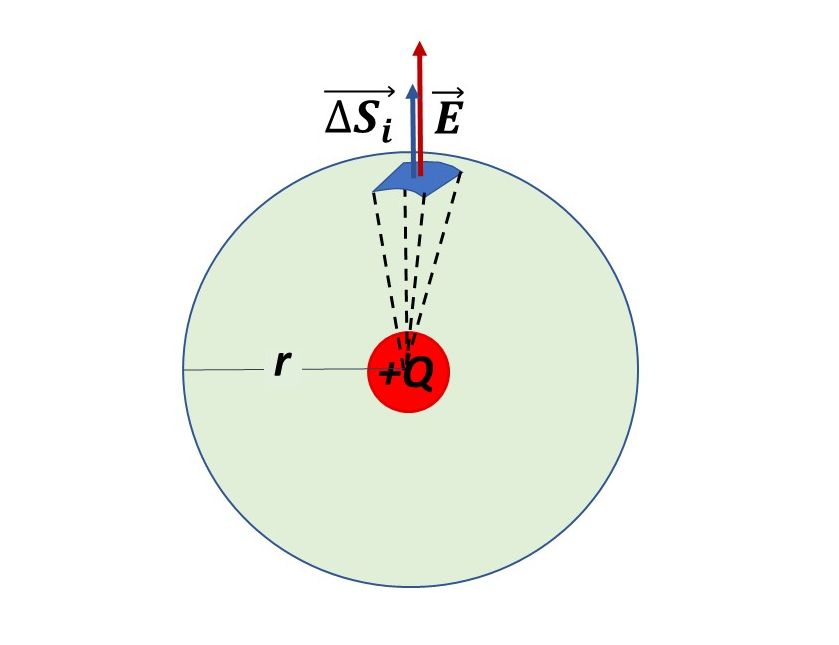
Neka je točkasti naboj
zatvoren unutar sferne plohe polumjera
i nalazi se u središtu te sfere. Tada je vektor jakosti električnog polja za svaku točku te plohe okomit na sfernu plohu. Iznos jakosti električnog polja je konstantan.
Cijelu plohu je moguće podijeliti na niz malih dijelova plohe. Odabran je jedan neizmjerno malen element na sfernoj plohi. Vektor jakosti električnog polja okomit je na taj element plohe.
Vektor normale ili vektor površine na element plohe također je okomit na element plohe i iznos mu je jednak ploštini tog elementa plohe
Iznos jakosti električnog polja točkastog naboja na udaljenosti od naboja dan je formulom
Jakost električnog polja i vekor površine paralelni su, pa je tok električnog polja kroz element plohe
Ukupan tok kroz cijelu sfernu plohu jednak je zbroju svih pojedinih tokova za elemenata ploha.
Ukupna ploština odgovara ploštini sfere
Slijedi da je ukupan tok električnog polja odnosno
ili
Taj oblik jednadžbe poznat je kao Gaussov zakon.
Gaussovim zakonom izražava se proporcionalnost ukupnog toka električnog polja i količine naboja unutar neke zatvorene plohe.
Ovisi li tok električnog polja o udaljenosti plohe
od naboja?
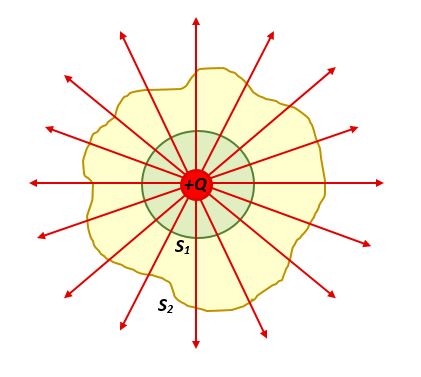
Ukupni električni tok ovisi samo o količini naboja zatvorenog unutar plohe. Bez obzira na oblik plohe koja okružuje naboj, ukupni tok električnog polja jednak je kroz sve plohe.
Pogledajmo u sljedećem pokusu što se događa s pozitivno nabijenom metalnom kuglicom ovješenom o nevodljivu nit, a koja se spušta kroz otvor nenabijene metalne sfere. Sfera je izolirana.
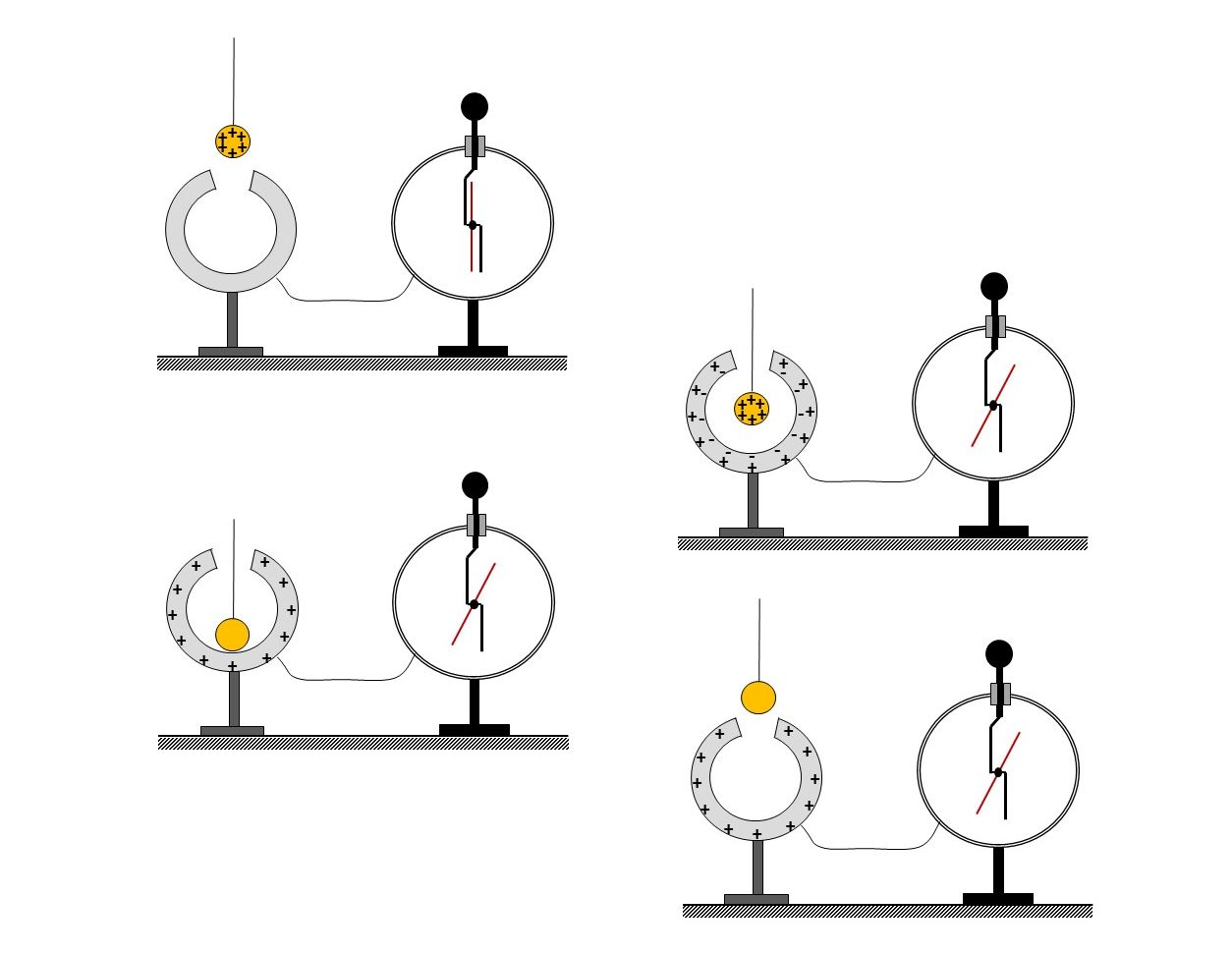
Za vrijeme spuštanja kuglice u unutrašnjost metalne sfere na sferi dolazi do razdvajanja naboja.
Pozitivno nabijena kuglica inducira negativne naboje s unutarnje strane metalne sfere, dok je na vanjskoj strani sfere
jednaka količina
Elektroskop je spojen na vanjsku stranu metalne sfere. Kazaljka elektroskopa se otklonila. Što pokazuje elektroskop?
Kuglica se dalje spušta unutar sfere sve dok ne dotakne njezino dno . U trenutku dodira dolazi do prijelaza naboja. Koliki je naboj kuglice?
Koliki je naboj unutarnje strane sfere?
Kazaljka elektroskopa je i dalje jednako otklonjena, što ukazjuje na to da je količina naboja s vanjske strane sfere
Metalna sfera radijusa elektrizirana je ukupnom kličinom naboja Naboj je jednoliko raspoređen po površini sfere. Odredite jakost električnog polja u točkama:
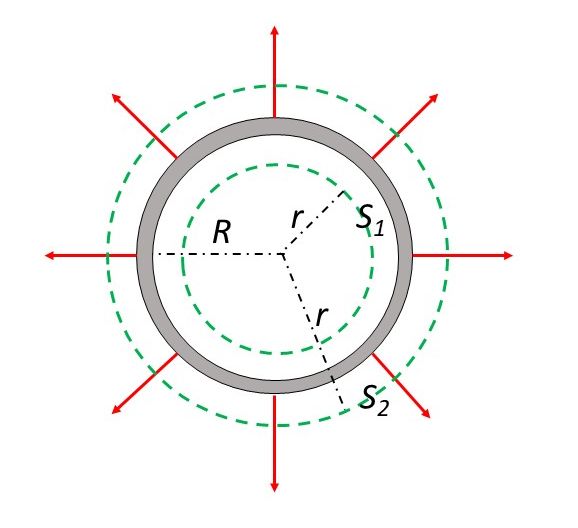
Naboji su jednoliko raspodijeljeni, pa električno polje mora biti simetrično. Ako su naboji pozitivni, silnice su usmjerene od površine sfere.
a. Izvan sfere,
Električne silnice su okomite na plohu metalne sfere i ukupna količina naboja unutar odabrane Gaussove plohe je Tok silnica električnog polja za odabranu Gaussovu plohu površine jednak je odnosno
Uvrštavanjem izraza za tok električnih silnica u Gaussov zakon
slijedi da je
i jakost električnog polja u nekoj odabranoj točki udaljenoj za od središta sfere, izvan sfere, iznosi
Takav iznos jakosti električnog polja dobili bismo i za slučaj da se naboj nalazi u središtu sfere.
b. Unutar sfere,
Električno polje je također radijalno simetrično. Količina naboja unutar Gaussove plohe
je nula,
.
Iz Gaussovog zakona slijedi da unutar metalne sfere nema polja,
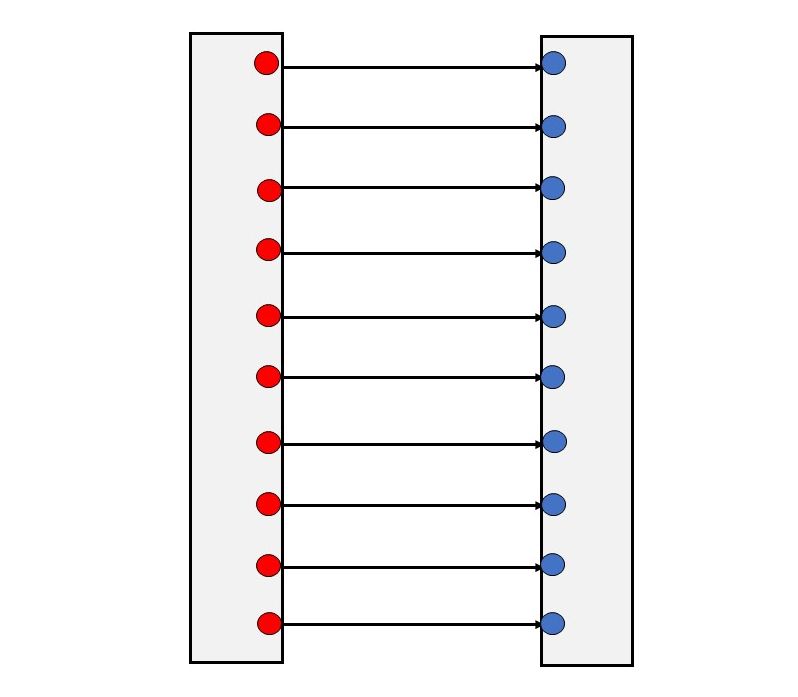
Imamo dvije tanke vrlo velike metalne ploče (mogli bismo reći beskonačno velike). Jedna je elektrizirana pozitivno, količinom naboja + (crveni kružići), a druga jednakom količinom naboja suprotnog predznaka, - (plavi kružići). Kako je ploča vodljiva, naboji se (zbog elektrostatskih odbijanja) preraspodjeljuju jednoliko na objema stranama ploča.
Električna polja jedne i druge elektrizirane ploče prikazana su na slici. Silnice izlaze (pozitivna ploča) odnosno poniru (negativna ploča) okomito na površine metalnih ploha.
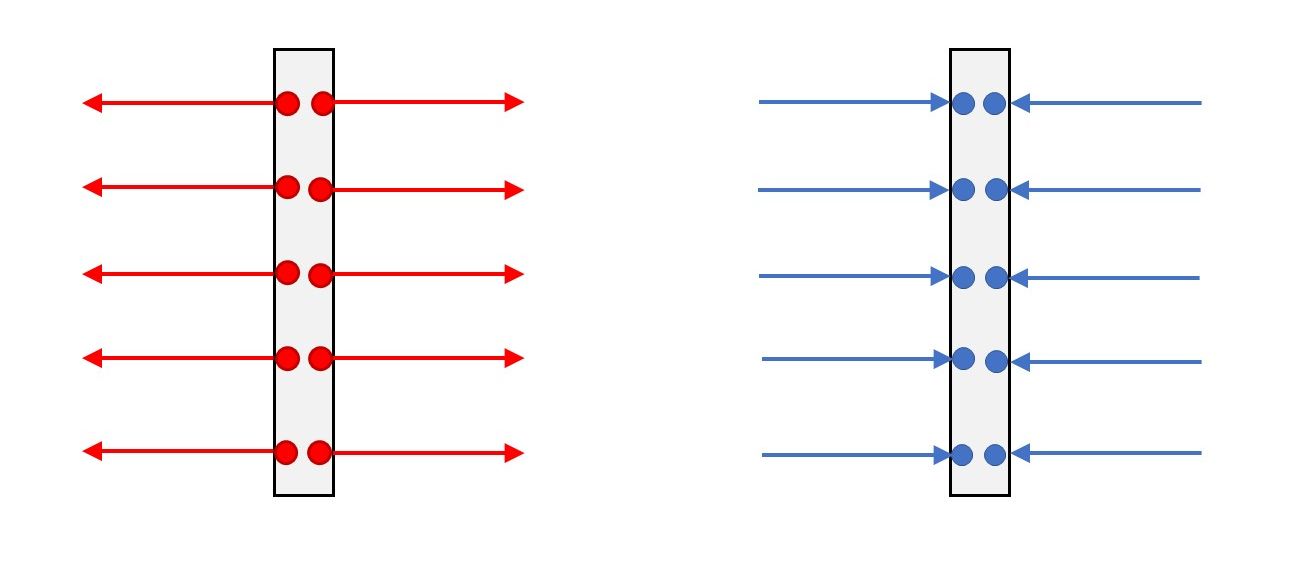
Ako približimo te dvije paralelno postavljene metalne ploče, dolazi do preraspodjele naboja. Zbog međusobnih elektrostatskih privlačenja naboji se preraspodjeljuju na unutarnjim stranama ploča.
Električno polje
između beskonačno velikih tankih metalnih ploča i u njihovu središnjem dijelu
homogeno je. Jakost i smjer električnog polja u svakoj točki takvog polja jednaki su. Izvan ploča nema električnog polja.
Površinska gustoća naboja određena je količinom naboja po jedinici površine
Mjerna jedinica za površinsku gustoću naboja je
Kakva je površinska gustoća naboja dviju paralelnih, tankih, beskonačno velikih ploča u odnosu na površinske gustoće pojedinačnih elektriziranih ravnih metalnih ploča?
Površinska gustoća je dva puta veća.
Što se dogodilo s jakošću električnog polja pri uspostavi opisanog homogenog električnog polja u odnosu na jakost električnog polja pojedinačne ploče?
Jakost električnog polja se dva puta povećala.
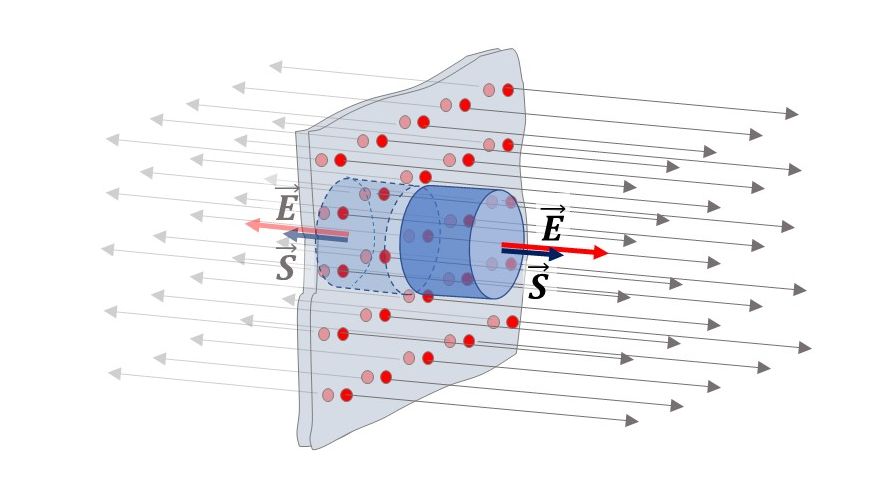
Na slici je prikazana tanka beskonačna pozitivno nabijena ploča. Naboji su jednoliko raspodijeljeni na objema plohama ploča.
Odaberimo cilindričnu Gaussovu plohu. Silnice prolaze kroz kružne plohe s jedne i s druge strane ploče. One ne prolaze kroz bočne plohe jer su im paralelne.
Vektor jakosti električnog polja stoga je okomit na plohu ploče.
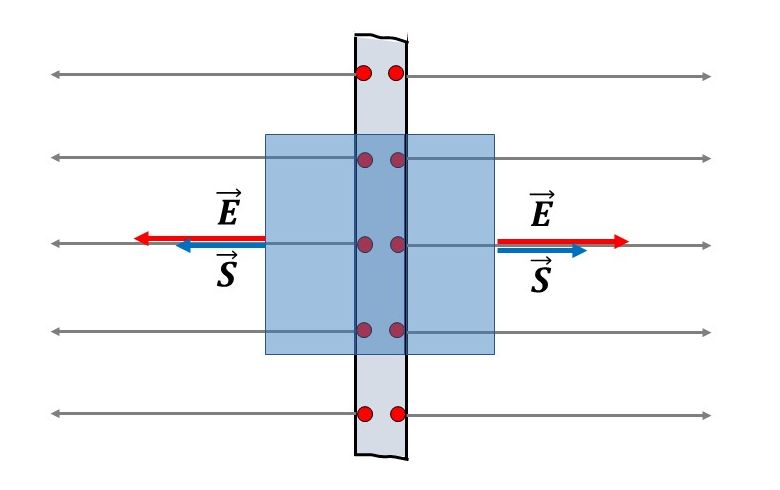
Radi jednostavnosti, razmatranje se može nastaviti i na osnovi dvodimenzionalnog prikaza Gaussove cilindrične plohe na slici.
Kroz samu metalnu ploču silnice ne prolaze. Može se pokazati da unutar vodiča električno polje ne postoji jer nema naboja. Naboji su raspodijeljeni samo po površini vodiča!
Odredimo ukupni tok groz cilindričnu Gaussovu plohu. Silnice prolaze samo kroz kružne plohe. Pretpostavka je da su odabrane dovoljno male površine da je jakost električnog polja konstantna.
Ukupni tok kroz kružne plohe (prednja i stražnja) je
Uvrstimo u Gaussov zakon
izraz za ukupni tok
i izrazimo naboj preko površinske gustoće
te uvrstimo u prethodni izraz:
Slijedi izraz za jakost električnog polja nabijene metalne ploče
.
Jakost električnog polja nabijene metalne ploče dana je formulom
U slučaju dviju suprotno nabijenih metalnih ploča koje smo približili uspostavlja se homogeno električno polje. Jakost tog električnog polja bit će dva puta veća u odnosu na električno polje nabijene metalne ploče.
Jakost električnog polja dviju nabijenih metalnih ploča dana je formulom
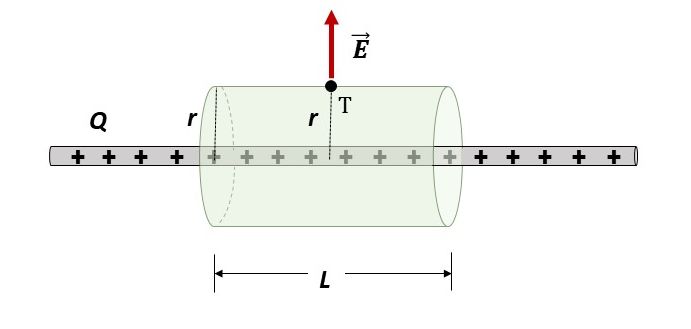
Uzduž vrlo duge ravne žice naboj je jednoliko raspodijeljen. Linijska gustoća naboja određena je omjerom količine naboja po jedinici duljine vodiča
Pokažite da se jakost električnog polja u točkama u blizini žice, dovoljno udaljenim od njezinih krajeva, može odrediti na osnovi izraza
Koristite se cilindričnom Gaussovom plohom prikazanom na slici:
Najzgodniji odabir Gaussove plohe je cilindrična ploha, jer je i žica cilindričnog oblika. Na slici u zadatku prikazana je cilindrična ploha polumjera baze
i visine
.
Silnice električnog polja ne prolaze kroz bazu odabrane Gaussove plohe, već samo kroz njezin plašt. Tok električnih silnica kroz baze je nula i one ne doprinose ukupnom toku kroz Gaussovu plohu.
Silnice električnog polja prolaze okomito površinom plašta čija je ploština jednaka
Ukupni tok električnih silnica određen je s odnosno
Ukupan naboj unutar zatvorene plohe prema Gaussovom zakonu je
Uvrštavanjem izraza za tok električnih silnica u Gaussov zakon
može se izraziti jakost električnog polja kao
Ako se u prethodni izraz uvrsti linijska gustoća naboja, dobiven je traženi oblik jednadžbe u zadatku:
.
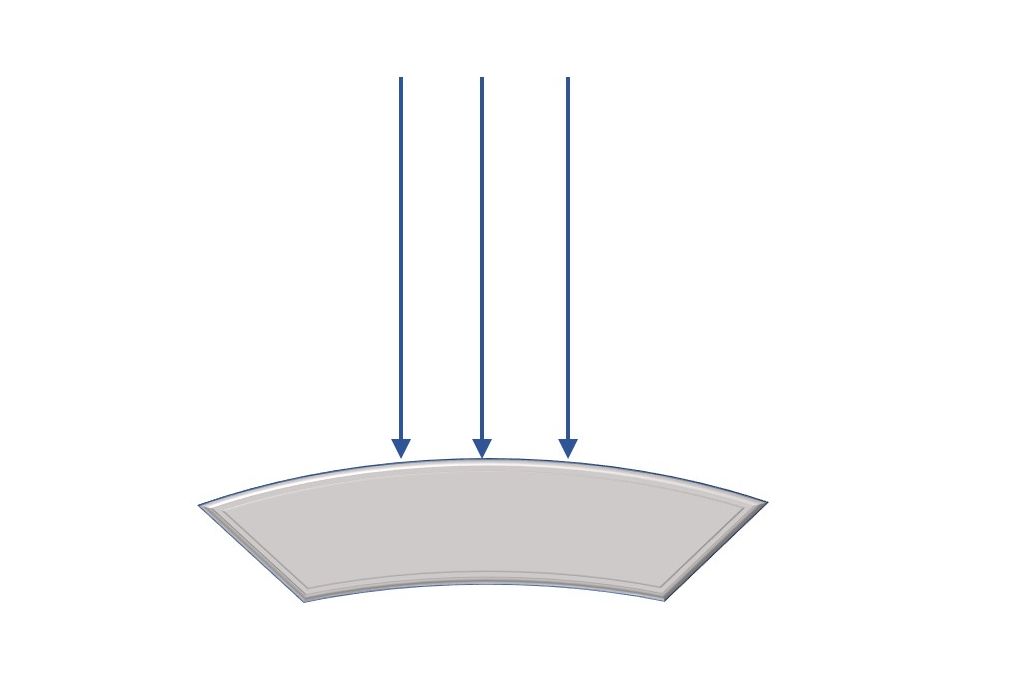
Crtež prikazuje silnice koje završavaju na metalnom tijelu. Odredite predznak naboja na tom metalnom tijelu.
Metal je negativno nabijen.
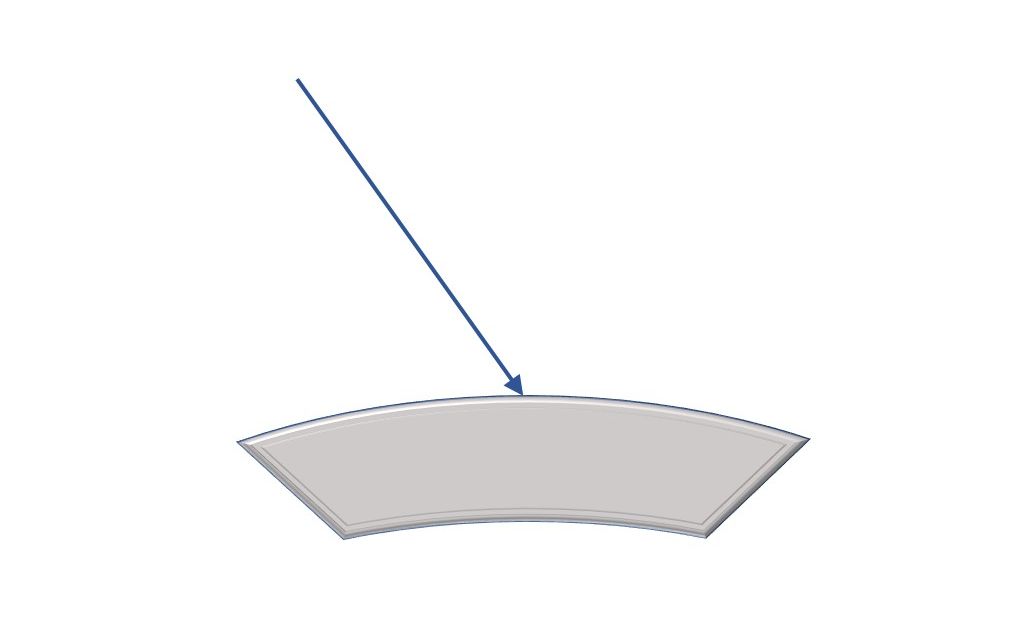
Kod elektrostatskog polja električne silnice su okomite na površinu vodiča. Zašto je tomu tako? Što bi se dogodilo kada silnice ne bi bile okomite?
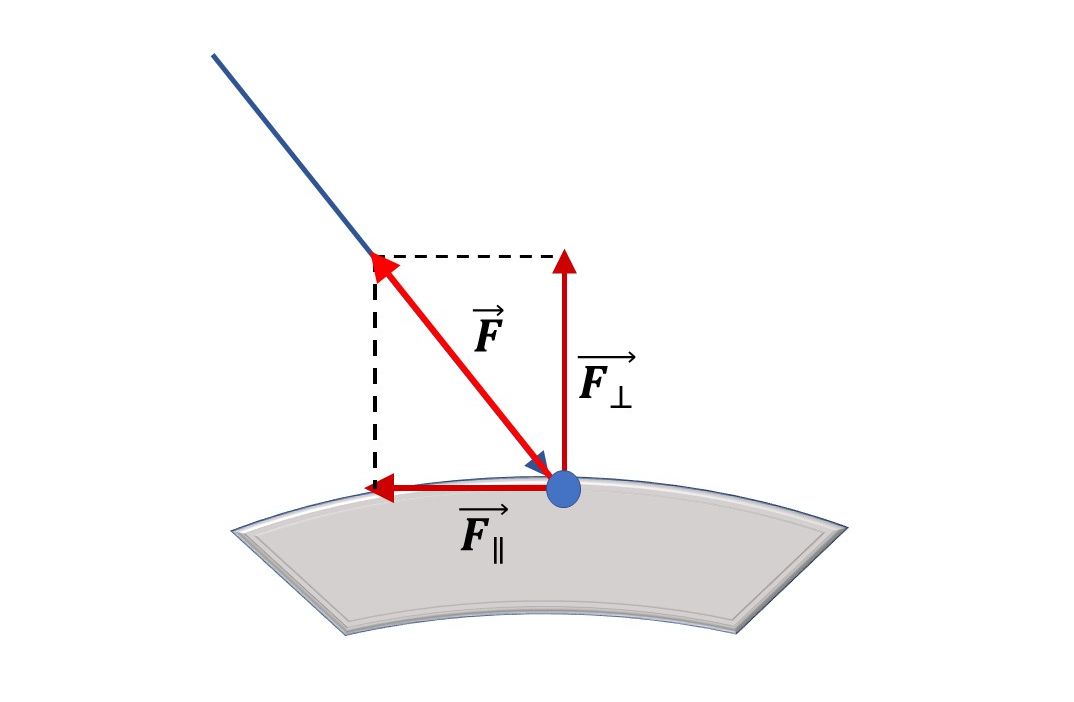
Vektor sile kojom se djeluje na elektron rastavi se na komponente.
Komponenta paralelna površini vodiča uvjetovat će gibanje naboja. Naboj će se gibati tako dugo dok se ne nađe u položaju da su silnice okomite na plohu vodiča. Uvjet elektrostatske ravnoteže je da su silnice okomite na površinu vodiča.
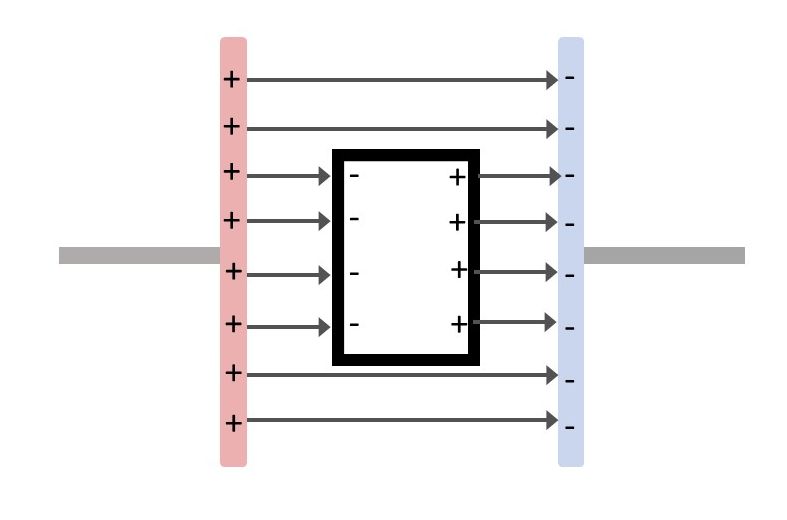
Michael Faraday je 1863. godine pokazao da se električna polja mogu zasjeniti ako se dio prostora unutar polja oklopi s pomoću vodiča, tzv. kavezom.
Faradayev kavez je zatvorena metalna ljuska ili metalna mreža na kojoj se naboji tako preraspodjeljuju da je jakost unutarnjeg električnog polja jednaka nuli.
Prikaz djelovanja Faradayeva kaveza dan je na slici.
To načelo posljedica je pojave da se slobodni naboji u vodiču zbog međusobnih elektrostatskih odbijanja raspodjeljuju po površini vodiča. Unutar vodiča polja nema.
Primjeri Faradayeva kaveza u svakodnevnom životu su vlak, avion, automobil.
Zaštita od neželjenih djelovanja električnih polja primjenjuje se i u slučaju koaksijalnih vodiča (antenski kabel, TV i radio prijenos). Često je potrebno zaštiti i elektroničke uređaje i sklopove.
U pokusima na videosnimkama prikazano je kako se mijenja raspodjela naboja na pravokutnoj savitljivoj žičanoj mreži pri njezinom savijanju i kako se raspodjeljuje naboj kada mreža ima oblik kaveza.
Pogledajmo jesmo li u Faradayevom kavezu kad smo u automobilu.
U slučajevima simetričnih raspodjela naboja jakost električnog polja se može odrediti primjenom Gaussovog zakona. Električnog polja unutar vodiča nema, a silnice električnog polja izlaze ili poniru okomito na plohu vodiča.
Tok silnica homogenog električnog polja koje prolaze kroz element površine određuje se prema izrazu gdje je komponenta vektora jakosti električnog polja okomita na površinu.
Prema Gaussovu zakonu ukupni tok električnih silnica kroz zatvorenu plohu proporcionalan je ukupnoj količini naboja zatvorenog unutar te plohe:
Jakost električnog polja određena primjenom Gaussovog zakona za neke simetrične raspodjele naboja:
jakost električnog polja između dviju suprotno nabijenih metalnih ploča,
blizu površine dugog ravnog vodiča (izolatora),
Gaussova sferna ploha zatvara električni dipol. Ukupni električni tok kroz sferu:
Tok električnog polja kroz zatvorenu površinu koja sadrži naboj količine
ne ovisi o: