Marko i Darko u svoju kasicu ubacuju kovanice. Marko je stariji i on ubacuje kovanice od 0.50 kn, a mlađi Darko u svoju kasicu ubacuje kovanice od 0.20 kn. Odlučili su se počastiti sladoledom čija je cijena 6 kn.
Koliko kovanica treba iz svoje kasice izvaditi Marko, ako će platiti 6 kuna, a koliko kovanica treba izvaditi Darko?
Da bismo odredili koliko kovanica iz svoje kasice mora izvaditi Marko, trebamo podijeliti 6 kn na kovanice od 0.50 kn. Budući da svaku kovanicu od 1 kn možemo zamijeniti s dvjema kovanicama od 0.50 kn, zaključujemo da će za iznos od 6 kn Marko izvaditi 12 kovanica od 0.50 kn.
Naravno, možemo si pomoći i pretvaranjem iznosa kuna u lipe pa dijeliti prirodan broj s prirodnim brojem.
6 kn:0.50 kn=600 lp:50 lp=12
Zaključujemo da je 6:0.50=600:50=12.
Da bismo odredili koliko kovanica iz svoje kasice mora izvaditi Darko, trebamo podijeliti 6 kn na kovanice od 0.20 kn. Budući da svaku kovanicu od 1 kn možemo zamijeniti s pet kovanica od 0.20 kn, zaključujemo da će za iznos od 6 kn Marko izvaditi 30 kovanica od 0.20 kn.
Naravno, možemo si pomoći i pretvaranjem iznosa kuna u lipe pa dijeliti prirodan broj s prirodnim brojem.
6 kn:0.20 kn=600 lp:20 lp=30
Zaključujemo da je
6:0.20=600:20=30.
Je li prethodne zadatke bilo moguće riješiti bez "usitnjavanja" kovanica ili bez pretvaranja mjernih jedinica?
Odgovor je, naravno, potvrdan. U ovoj ćeš jedinici naučiti kako se prirodni i decimalni brojevi dijele s decimanim brojem.
Podsjeti se svojstva dijeljenja prirodnih brojeva.
Pomnožimo li i djeljenik i djelitelj istim brojem, količnik se neće promijeniti.
Primjer 1.
Djed je sa svojim unucima nabrao 168 kg šljiva. Koliko je kanti potrebno djedu i unucima u branju ako u svaku kantu stane 10.5 kg šljiva?
168 kg:10.5 kg=16 800 dag:1 050 dag=16
Djed i unuci napunili su
16 kanti.
Zapisano bez mjernih jedinica:
168:10.5=16 800:1 050.
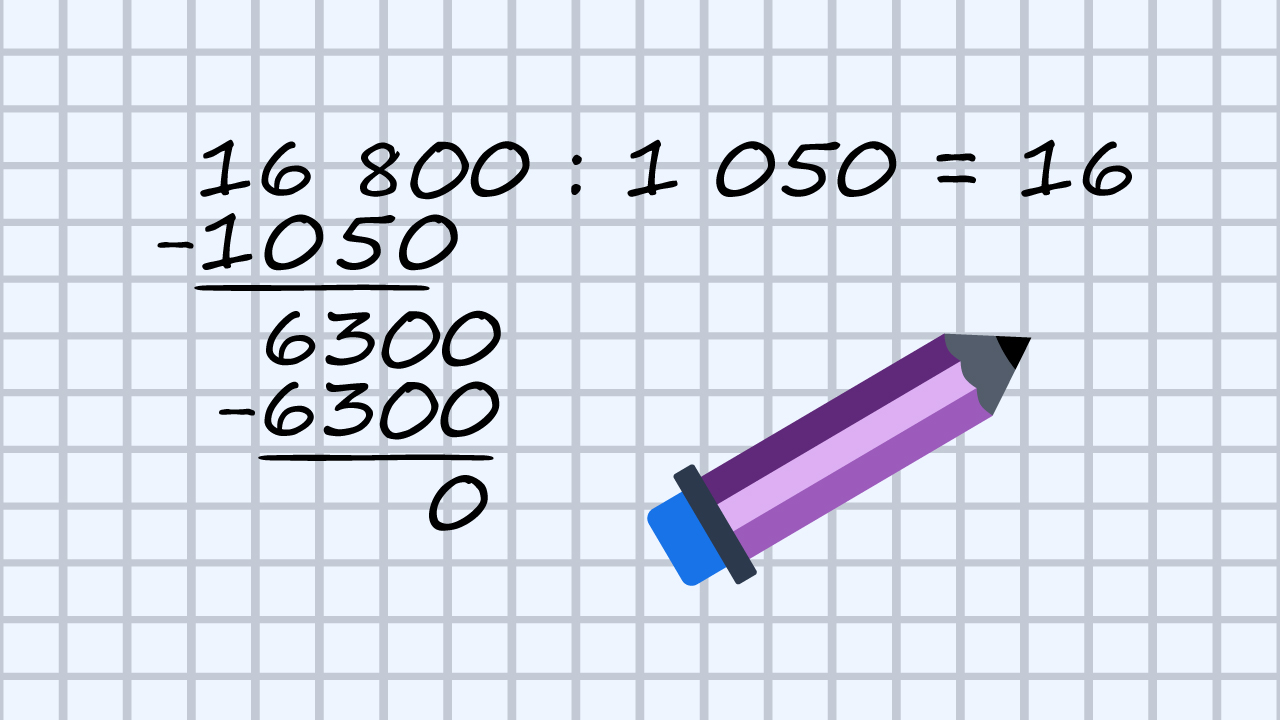
Primjer 2.
Majka je napravila 9 litara soka od bazge. Sokom je punila boce volumena 0.75 litre. U koliko će boca majka rasporediti sok od bazge?
9 l:0.75 l=90 dl:7.5 dl=900 cl:75 cl=12
Majka će sok rasporediti u 12 boca volumena 0.75 litre.
Ako u zapisu izostavimo mjerne jedinice, dobivamo da je 9:0.75=900:75
Iz prethodnih primjera zamjećujemo da je količnik prirodnog i decimalnog broja ostao isti nakon što smo i djeljenik i djelitelj pomnožili s istom dekadskom jedinicom, tj. nakon što smo decimalnu točku u djeljeniku i djelitelju pomaknuli udesno za isti broj decimala.
Da se količnik ne bi promijenio, istom dekadskom jedinicom trebamo pomnožiti i djeljenik i djelitelj.
Matko u dvorištu ima vrt u obliku pravokutnika površine
18 m2. Da bi zaštitio posađeno povrće od svojega nestašog psa, odlučio je oko vrta staviti ogradu. S majstorom Perom dogovara izradu ograde, no majstor kaže da mu podatak o površini nije dovoljan i da treba znati duljinu i širinu vrta.
Matko zna da je vrt dug
4.8 m, no širine se nije mogao sjetiti! Mora li se vraćati kući izmjeriti širinu vrta ili majstor Pero može napraviti dobru ogradu na osnovi poznatih podataka?
Kolika je širina vrta?
Koliki je opseg tog vrta?
Površina pravokutnika jednaka je umnošku duljina duljine i širine vrta pa će majstor Pero uspjeti napraviti potrebnu ogradu.
Dakle, širinu vrta doznat ćemo tako da podijelimo površinu pravokutnika s njegovom duljinom, tj. tako da izračunamo koliko je
18 m2:4.8 m.
Ovaj put nećemo pretvarati mjerne jedinice nego primijeniti uočeno svojstvo - djeljenik i djelitelj pomnožit ćemo s brojem
10 (tako da djelitelj postane prirodan broj), a zatim ćemo umjesto
18:4.8 izračunati količnik
180:48.
Budući da je 180:48=3.75, zaključujemo da je 18:4.8=3.75, što znači da je širina vrta 3.75 m.
Opseg vrta jednak je zbroju duljina njegovih stranica. Budući da je
2·(4.8+3.75)=2·8.55=17.1, zaključujemo da je opseg vrta
17.1 m.
Promotrimo još jedanput račune iz prethodnih primjera i zadatka.
9:0.75=900:75
168:10.5=16 800:1 050=1 680:105
18:4.8=180:48
Prirodne brojeve dijelimo s decimalnim brojevima tako da prirodnom broju dopišemo onoliko nula za koliko se mjesta pomiče decimalna točka u djelitelju kada ga pretvaramo u prirodan broj, a zatim dijelimo prirodan broj s prirodnim brojem.
Uz jedan rub ulice duge 1.53 km stanovnici žele posaditi lipe. Stručnjaci su im savjetovali da udaljenost između dvaju stabala bude 42.5 m. Koliko sadnica trebaju kupiti?
Da bismo doznali koliko sadnica treba kupiti, duljinu ulice ( 1.53 km=1 530 m) treba podijeliti na jednake razmake ( 42.5 m). Broj razmaka između sadnica je
1 530 m:42.5 m=15 300 dm:425 dm=36.
Broj potrebnih sadnica je za 1 veći od broja razmaka (sadnica treba biti i na početku i na kraju ulice), pa treba nabaviti 37 sadnica.
Primjer 3.
Paketić Njami bombona prodaje se po cijeni od 4.65 kn. Iva je za bombone potrošila ukupno 18.60 kn. Koliko je paketića bombona kupila?
Broj kupljenih paketića izračunat ćemo dijeljenjem potrošenog iznosa s cijenom jednog paketića bombona. Pomoći ćemo si pretvaranjem podataka u manju mjernu jedinicu, lipe.
18.60 kn:4.65 kn=1 860 lp:465 lp=4
Iva je kupila 4 paketića bobmona.
Zaključujemo da je
18.60:4.65=1 860:465=4.
Pri dijeljenju decimalnog broja s decimalnim brojem pomogli smo si pretvaranjem mjernih jedinica, no mogli smo i drukčije: pomnožiti i djeljenik i djelitelj istom dekadskom jedinicom tako da djelitelj postane prirodni broj.
To znači da prije dijeljenja decimalnu točku u djeljeniku i djelitelju pomičemo udesno za isti broj mjesta tako da djelitelj postane prirodan broj.
Primjer 4.
Marjana je 0.7 kg puretine platila 29.89 kn. Kolika je cijena kilograma puretine?
Da bismo doznali cijenu kilograma puretine potrebno je plaćeni iznos podijeliti s masom kupljenog mesa. Prije dijeljenja
29.89:0.7 djeljenik i djelitelj pomnožimo s brojem
10, tj. decimalnu točku u djeljeniku i djelitelju pomaknemo za jedno mjesto udesno pa dijelimo
298.9:7. Računamo:
29.89:0.7=298.9:7=42.7.
Cijena kilograma kupljene puretine je 42.7 kn.
Majka je
2.2 m tkanine platila
236.28 kn. Kolika je cijena metra te tkanine?
Da bismo odredili cijenu jednog metra te tkanine, moramo plaćeni iznos podijeliti s količinom (duljinom) kupljene tkanine.
236.28:2.2=2362.8:22=107.4
Cijena jednog metra kupljene tkanine je
107.4 kn.
Primjer 5.
U kutiji je 3.5 dag šećera s okusom limuna. Prema receptu za limunove keksiće na svaki keksić prije pečenja treba staviti 0.1 dag takvog šećera. Koliko se keksića može pripremiti s toliko šećera?
Broj keksića dobit ćemo dijeljenjem 3.5:0.1 ili, nakon pomicanja decimalne točke u djeljeniku i djelitelju za jedno mjeto udesno, dijeljenjem 35:1.
Sa spomenutom količinom šećera možemo napraviti
35 keksića.
Primjer 6.
Izračunajmo.
a) 2.75:0.1
b) 1.25:0.01
c) 1.3:0.001
a)
2.75:0.1=27.5:1=27.5
b)
1.25:0.01=125:1=125
c)
1.3:0.001=1 300:1=1 300
Decimalni broj dijeli se s dekadskom jedinicom manjom od 1 tako da decimalnu točku u zadanom broju pomaknemo udesno za onoliko mjesta koliko decimala ima dekadska jedinica s kojom dijelimo.
Decimalni broj množi se s dekadskom jedinicom (većom od 1) tako da se decimalna točka u zadanom broju pomakne udesno za onoliko mjesta koliko nula ima dekadska jedinica s kojom množimo. Dakle, na isti se način množi s dekadskom jedinicom većom od 1 i dijeli s dekadskom jedinicom manjom od 1.
Primjer 7.
1.23·10=1.23:0.1=12.3
34.7·100=34.7:0.01=3 470
2.8·1 000=2.8:0.001=2 800
Izračunaj.
Podijelimo li decimalan broj sa samim sobom, količnik je jednak 1.
Izračunaj.
Podijelimo li decimalan broj s brojem 1, količnik je jednak djeljeniku.
Izračunaj.
Istražimo
Odaberi još nekoliko parova različitih decimalnih brojeva a, b pa s pomoću džepnog računala izračunaj oba količnika, a:b i b:a. Što zamjećuješ? Jesu li dobiveni količnici jednaki?
Dijeljenje decimalnih brojeva nije komutativno, tj. za dva različita decimalna broja vrijedi a:b≠b:a.
Izračunaj.
Istražimo
Odaberi još nekoliko trojki različitih decimalnih brojeva a, b, c pa s pomoću džepnog računala izračunaj količnike a:(b:c) i (a:b):c. Što zamjećuješ? Jesu li dobiveni količnici jednaki?
Dijeljenje decimalnih brojeva nije asocijativno, tj. za tri različita decimalna broja a, b, c vrijedi a:(b:c)≠(a:b):c.
Pri rješavanju zadataka u sljedećoj kolekciji možeš se služiti džepnim računalom. Rješenja zadataka zaokruži na najbližu desetinku.
Uvježbaj dijeljenje decimalnih brojeva.
