Matematika 5 - 2.5 Množenje prirodnih brojeva

Na početku...

Petar je od kartona izradio polje za igru, a iz drveta dijelove slagalice. Igru je nazvao Algebris. Igra se tako da polje za igru treba u potpunosti i bez preklapanja prekriti drvenim dijelovima. Dijelovi slagalice prikazani su slikom. Od koliko se kvadratića sastoji polje za igru Algebris?

$10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 120$

Kraće možemo zapisati $12 \cdot 10 = 120 .$

Polje za Algebris sastoji se od $120$ kvadratića.

Množenje prirodnih brojeva možemo shvatiti kao uzastopno zbrajanje jednakih pribrojnika.

Brojeve koje množimo zovemo faktori, a rezultat množenja zovemo umnožak ili produkt.

Zadatak 1.

Pomoću apleta ponovi tablicu množenja do $100 .$

Istražimo

Niko i Vid osmislili su igru s igraćom kockicom. Igrači bacanjem novčića odabiru koji će igrač biti prvi, a koji drugi. Prvi igrač bira hoće li biti par ili nepar. Prvi igrač baca kockicu i zapisuje broj koji je dobio. Drugi igrač baca kockicu i zapisuje broj koji je dobio. Dobiveni brojevi tada se množe. Ako je umnožak paran, bod dobiva igrač koji je odabrao biti par. Ako je umnožak neparan, bod dobiva igrač koji je odabrao biti nepar. Je li igra pravedna? Istraži i objasni.

Igra nije pravedna.

Množenjem dvaju parnih brojeva dobit ćemo paran broj.

Množenjem parnog i neparnog te neparnog i parnog također ćemo dobiti paran broj.

Jedino u slučaju množenja dvaju neparnih brojeva dobit ćemo neparan broj.

To znači da u tri puta više slučajeva možemo dobiti paran broj.

Zadatak 2.

Je li umnožak dvaju prirodnih brojeva uvijek prirodni broj?

Da

Ne

null

null
Kako se naziva rezultat množenja?

null

null
Kako se nazivaju brojevi koje množimo?

null

null

Primjer 1.

Izračunajmo.

a) $234 \cdot 1$

b) $0 \cdot 3 473$

c) $54 \cdot 10$

d) $974 \cdot 100$

e) $46 \cdot 1 000$

a) $234 \cdot 1 = 243$

b) $0 \cdot 3 473 = 0$

c) $54 \cdot 10 = 540$

d) $974 \cdot 100 = 97 400$

e) $46 \cdot 1 000 = 46 000$

Množimo li neki prirodni broj brojem $10,$ umnožak dobivamo tako da početnom faktoru zdesna dopišemo jednu nulu. Kod množenja brojem $100$ početnom broju zdesna dopišemo dvije nule, kod množenja brojem $1 000$ broju zdesna dopisujemo tri nule itd.

Kolekcija zadataka #1

Izračunaj.

$56 \cdot 10 000 =$
$7 \cdot 8 \cdot 11 \cdot 0 \cdot 2 =$
$1 \cdot 4 567 826 =$
$0 \cdot 0 =$

null

Pretvori mjerne jedinice.

$9 km =$

m

null

$17 dm =$

mm

null

$7 cm =$

mm

null

$4 t =$

kg

null

$3 kg =$

dag

null

Primjer 2.

Izračunajmo.

a) $34 \cdot 20$

b) $250 \cdot 30$

c) $60 \cdot 8 000$

d) $320 \cdot 400$

a) Broj $34$ množimo s brojem $20$ tako da ga prvo pomnožimo s brojem $2,$ a zatim s brojem $10 .$ To zapravo znači da $34$ pomnožimo s brojem $2$ i dopišemo jednu nulu.

$34 \cdot 20 = 680$

b) Broj $250$ množimo s brojem $30$ tako da pomnožimo $25$ s brojem $3$ te dopišemo dvije nule ( $10 \cdot 10 = 100$ ).

$250 \cdot 30 = 7 500$

c) Broj $60$ množimo s brojem $8 000$ tako da pomnožimo $6$ s brojem $8$ te dopišemo četiri nule.

$60 \cdot 8 000 = 480 000$

d) Broj $320$ množimo s brojem $400$ tako da pomnožimo $32$ s brojem $4$ te dopišemo tri nule.

$320 \cdot 400 = 128 000$

Zadatak 3.

Poveži zadatak i njegovo rješenje.

$210 \cdot 400$	$840$
$210 \cdot 40$	$8 400$
$210 000 \cdot 4$	$840 000$
$21 \cdot 40$	$84 000$

null

Kvadrati prirodnih brojeva do 10

Primjer 3.

Izračunajmo površinu kvadrata sa stranicom duljine:

a) $5 cm$

b) $7 m .$

a) Površinu kvadrata računamo tako da pomnožimo duljine dviju susjednih stranica. Stranice kvadrata jednakih su duljina te stoga množimo $5$ s $5 .$

$p = 5 \cdot 5 = 25 {cm}^{2}$

b) $p = 7 \cdot 7 = 49 m^{2}$

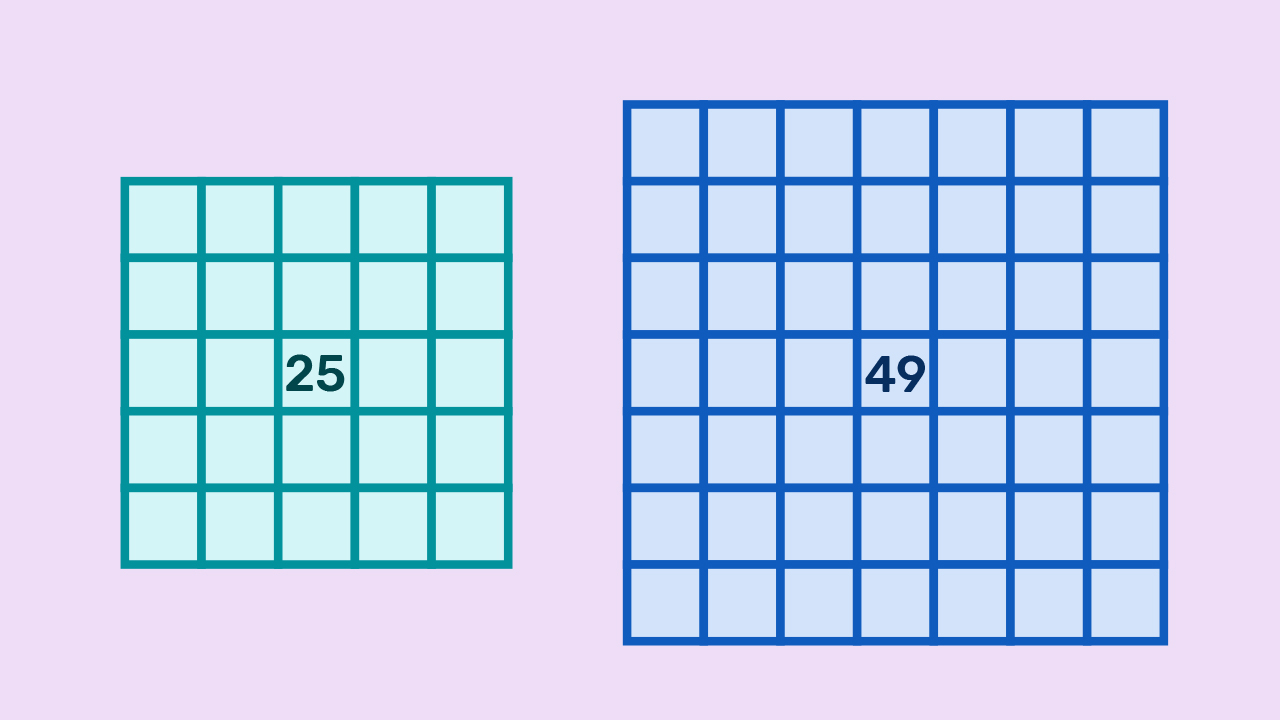
Dva kvadrata. Prvi se sastoji od 25 manjih kvadratića, dok se drugi sastoji od 49 manjih kvadratića. — Dva kvadrata

U svakom od zadataka množili smo broj sa samim sobom. Izraz poput $5 \cdot 5$ kraće možemo zapisati $5^{2}$ te ga čitamo "pet na kvadrat".

Kvadriranje

Kvadrirati broj znači pomnožiti broj sa samim sobom.

$a \cdot a = a^{2}$

Zadatak 4.

Poveži zadatak i njegovo rješenje.

$9^{2}$	$64$
$8^{2}$	$81$
$10^{2}$	$36$
$6^{2}$	$100$

null

Zadatak 5.

Uvježbaj određivanje kvadrata prirodnih brojeva do $100$ igrajući igru memorije.

Povećaj interaktivni prikaz

Množenje pomoću modela površine

Promotrimo množenje dvoznamenkastog broja s jednoznamenkastim brojem pomoću modela površine pravokutnika.

Prisjetimo se pritom da površinu možemo shvatiti kao broj jediničnih kvadratića kojima možemo prekriti neki geometrijski lik.

Primjer 4.

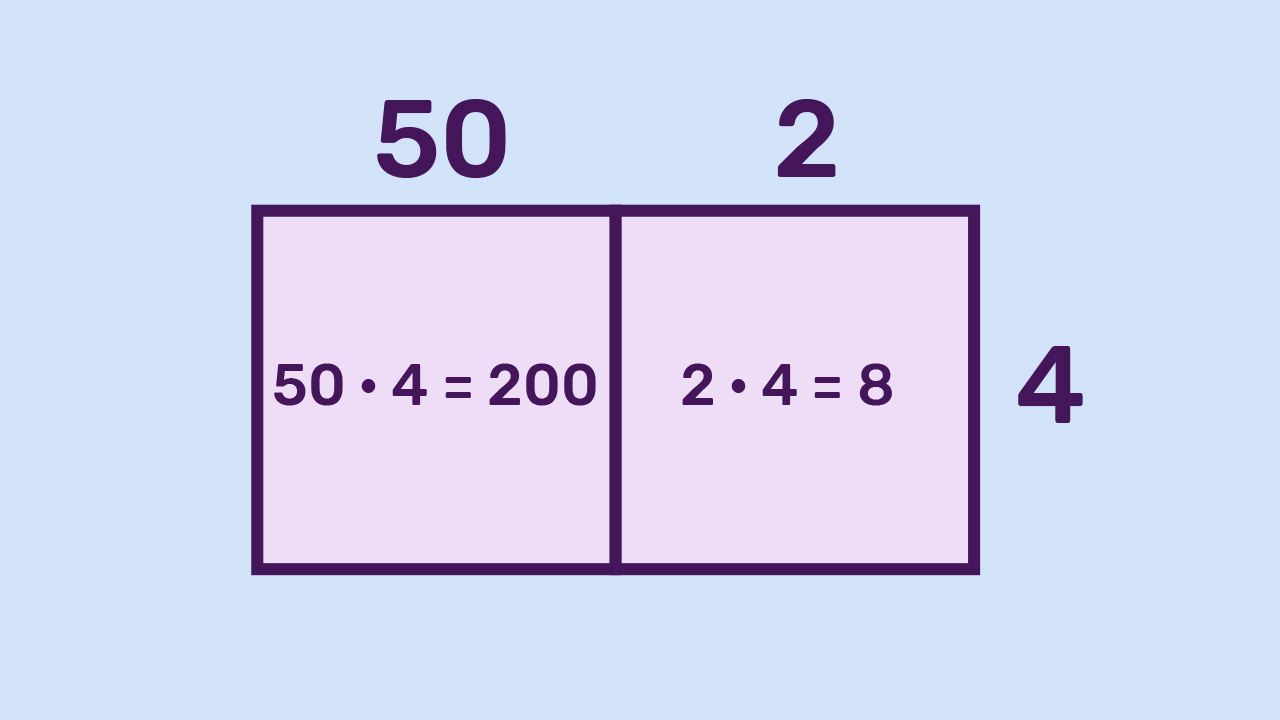
Izračunajmo $52 \cdot 4 .$

Prvo prikažimo množenje modelom pravokutnika.

Broj $52$ sastoji se od $5$ desetica i $2$ jedinice. Možemo ga stoga rastaviti na $5 D + 2 J,$ tj. $50 + 2 .$

Pomnožimo li $50$ s $4$ dobit ćemo $200,$ a pomnožimo li $2$ s $4$ dobit ćemo $8 .$ Stoga je $(50 + 2) 4 = 200 + 8 = 208 .$

Veliki pravokutnik koji je podijeljen na dva manja. Iznad lijevog pravokutnika piše broj 50 i unutar njega je jednadžba 50x4=200. Iznad drugog pravokutnika je broj 2 i unutar njega je jednadžba 2x4=8. Desno od velikog pravokutnika nalazi se broj 4. — Množenje modelom pravokutnika

Primjer 5.

Pisanim putem pomnožimo brojeve $52$ i $4 .$

Pisano množenje
S		D	J	$\cdot$	J
		$5$	$2$		$4$
	$↶$
$2$		$2$ $0$	$8$
$2$		$0$	$8$
ili kraće
S		D	J	$\cdot$	J
		$5$	$2$		$4$
$2$		$0$	$8$

Zadatak 6.

Pomoću apleta modela površine istraži množenje troznamenkastog i jednoznamenkastog broja.

Primjer 6.

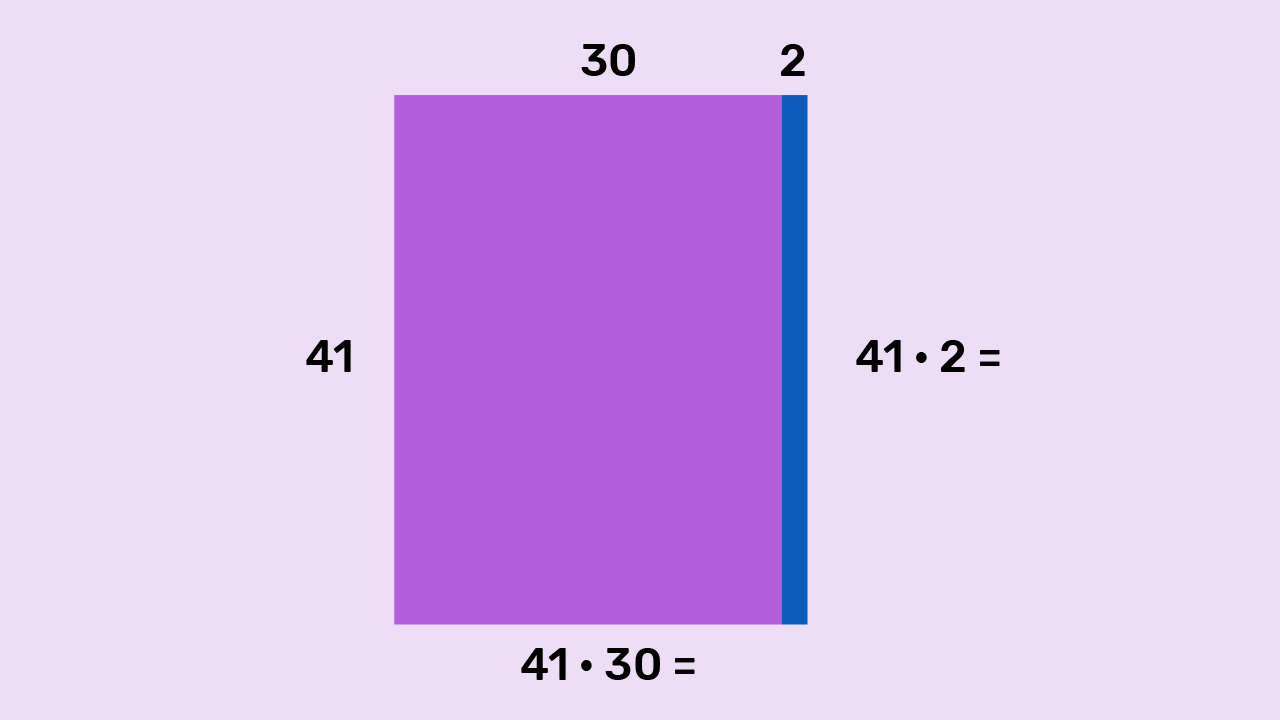
Izračunajmo umnožak $41 \cdot 32 .$

Drugi faktor, broj $32$ možemo rastaviti na $30 + 2 .$ Površina prvog pravokutnika jednaka je $41 \cdot 30 = 1 230,$ a drugoga $41 \cdot 2 = 82$ te je ukupna površina $1 312$ (jer je $1 230 + 82 = 1 312$ ).

Veliki pravokutnik koji se sastoji od dva manja. Iznad ljubičastog pravokutnika piše broj 30, lijevo od tog pravokutnika je broj 41, a ispod njega je jednadžba 41x30=. Iznad plavog pravokutnika piše broj 2, a desno od tog pravokutnika je jednadžba 41x2= . — Pravokutnici 41*32

Primjer 7.

Pisanim putem pomnožimo brojeve $41$ i $32 .$

Pisano množenje $41 \cdot 32$
	S	D	J	$\cdot$	D	J
		$4$	$1$	$\cdot$	$3$	$2$
	$1$	$2$	$3$	$0$
$+$			$8$	$2$
	$1$	$3$	$1$	$2$

Zadatak 7.

Dodatno uvježbaj množenje dvoznamenkastih brojeva koristeći se sljedećim apletom i modelom površine kao pomoći pri radu. Aplet drugi faktor rastavlja na dva pribrojnika, svaki od njih treba pomnožiti s prvim pribrojnikom, a zatim dobivene umnoške zbrojiti. Ako trebaš pomoć, odaberi mogućnost prikazivanja međukoraka.

Postupak množenja prirodnih brojeva

Promotrimo postupak množenja promatrajući mjesne vrijednosti.

Primjer 8.

Pomnožimo broj $402$ s brojem $312 .$

Višeznamenkaste brojeve množimo tako da prvi faktor prvo pomnožimo sa znamenkom najveće mjesne vrijednosti drugog faktora. U ovom slučaju znamenkom stotica, $3 .$ S obzirom na to da množimo s $3$ stotice, zapravo množimo s brojem $300$ te je umnožak $120 600 .$ Nakon toga prvi faktor množimo sa znamenkom desetica, što je u ovom slučaju $1.$ Pomnožiti s $1$ deseticom zapravo znači pomnožiti s $10$ te je umnožak $4 020 .$ Konačno, prvi faktor množimo sa znamenkom jedinica. U ovom slučaju to je $2$ te je umnožak $804 .$ Konačno, zbrajamo dobivene brojeve.

$120 600 + 4 020 + 804 = 125 424$

Primijeti, nule koje pišemo na kraju ne mijenjaju ukupan zbroj na pojedinoj mjesnoj vrijednosti te ih obično ne pišemo, već se u svakom sljedećem redu pomičemo za jedno mjesto udesno.

Pisano množenje $402 \cdot 312$
	T	S	D	J	$\cdot$	S	D	J
		$4$	$0$	$2$	$\cdot$	$3$	$1$	$2$
	$1$	$2$	$0$	$6$
			$4$	$0$	$2$
$+$				$8$	$0$	$4$
	$1$	$2$	$5$	$4$	$2$	$4$

Zadatak 8.

Lanac zadataka i rješenja

Poredaj kartice po redu tako da rješenje prve kartice odgovara broju pri vrhu druge kartice, rješenje druge kartice odgovara broju pri vrhu treće kartice itd.

Rješenje prethodne kartice: $22 044$
Zadatak: $53 \cdot 33$
Rješenje prethodne kartice: $14 271$
Zadatak: $32 \cdot 74$
Rješenje prethodne kartice: $9 369$
Zadatak: $102 \cdot 217$
Rješenje prethodne kartice: $1 749$
Zadatak: $71 \cdot 201$
POČETNA KARTICA
Zadatak: $56 \cdot 103$
Rješenje prethodne kartice: $22 134$
Zadatak: $7 \cdot 423$
Rješenje prethodne kartice: $2 961$
Zadatak: $44 \cdot 501$
Rješenje prethodne kartice: $5 768$
Zadatak: $27 \cdot 347$

null

Primjena množenja prirodnih brojeva

Zadatak 9.

Petrina mama želi prestati pušiti. Ako Petrina mama dnevno kupi jednu kutiju cigareta po cijeni od $27 kn,$ koliko će uštedjeti nakon:

a) tjedan dana

b) mjesec dana ( $30$ dana)

c) godinu dana od prestanka pušenja?

a) $27 \cdot 7 = 189 kn$

b) $27 \cdot 30 = 810 kn$

c) $27 \cdot 365 = 9 855 kn$

Kolekcija zadataka #2

Marina promatra svoju mjesečnu potrošnju kako bi mogla bolje upravljati svojim financijama. Marina je zaključila da je ručkovi koje jede na poslu koštaju $35$ kuna po obroku. Ako je Marina u rujnu radila $23$ dana, koliko je potrošila na ručkove na poslu?

Marina je za ručkove na poslu potrošila

kn .

null

U školskoj knjižnici knjige su složene u jednake ormare s policama. Ormari imaju ukupno $24$ police, a na svakoj polici složeno je $207$ knjiga. Koliko knjiga ima knjižnica?

Školska knjižnica ima

knjiga.

null

Robertu se pokvario automobil. Automehaničar sat rada naplaćuje $268$ kn. Cijena dijelova koje Robert mora zamijeniti iznosi $2 456$ kn, a automehaničar će mu naplatiti $12$ sati rada.

Robert će popravak svog automobila morati platiti

kn .

Pomoć:

Koliko će Robert morati platiti za rad, a koliko za dijelove? Ukupan iznos koji će Robert platiti jedanak je zbroju tih dvaju iznosa.

Postupak:

$268 \cdot 12 + 2 456 = 3 216 + 2 456 = 5 672$

Ana redovito vježba te razmišlja bi li uplatila članarinu za fitness centar za cijelu godinu jednokratno, mjesečno ili tromjesečno.

Cijene pojedine vrste članarine prikazane su tablicom.

Mjesečna članarina	Tromjesečna članarina	Godišnja članarina
$260 kn$	$660 kn$	$2 400 kn$

Ako Ana uplatu vrši svaki mjesec, godišnju članarinu platit će

kn .

Ako Ana uplatu vrši jednom u svaka tri mjeseca, godišnju članarinu platit će

kn .

Cijena najpovoljnije članarine za

kn

je manja od cijene najskuplje članarine.

null

Na sastanku stanara raspravlja se o ugradnji dizala. Predstavnik stanara rekao je da je dobio izračun po kojem bi se pričuva svakog stana povećala za $234 kn$ mjesečno tijekom razdoblja od $15$ godina.

Ako zgrada ima

12

stanova, ukupna cijena ugradnje dizala iznosi

kn .

null

Rene ima disleksiju i mora ići na logopedske vježbe. Cijena sata logopedske terapije je

160 kn .

Nakon procjene, logoped je ustanovio da će Rene morati dolaziti dva puta tjedno sljedećih pet mjeseci, što je ukupno

40

dolazaka.

Rene će ukupno platiti logopedske vježbe

kn .

null

Procjena

Ponekad nam nije potrebno precizno rješenje nego nam je procjena dovoljna. Procjena nam također pomaže pri provjeri smislenosti naših rješenja.

Primjer 9.

Robertina želi kupiti poklone za svoje poslovne prijatelje. Treba joj $28$ poklona. Na polici dućana ugledala je poklon kakav je željela. Cijena jednog poklona iznosi $148 kn .$ Kako će Robertina procijeniti koliko ukupno treba platiti poklone? Objasni.

Robertina može cijenu poklona zaokružiti na $150 kn,$ a broj poklona na $30 .$ Tada jednostavno može izračunati umnožak tih dvaju brojeva. $150 \cdot 30 = 4 500$ Robertina će poklone za svoje poslovne partnere platiti oko $4 500 kn .$

Zadatak 10.

Marino se bavi organizacijom vjenčanja. S klijentom je odabrao cvjetne aranžmane koji će biti postavljeni na svaki od $27$ stolova. Cijena svakog takvog cvjetnog aranžmana iznosi $122 kn .$ Klijent ga je pitao kolika će biti približna ukupna cijena aranžmana koje trebaju naručiti za stolove. Koju procjenu Marino treba dati svojem klijentu? Objasni.

Marino može broj stolova zaokružiti na $30,$ a cijenu aranžmana na $120 kn .$ Množenjem brojeva $30$ i $120$ dobit će $3 600 .$ Ukupna cijena aranžmana iznosit će približno $3 600 kn$ .

Kolekcija zadataka #3

Procijeni umnožak.

$210 \cdot 128 =$
.
$1 003 \cdot 496 =$
.

null

Slastičarnica Slatki užitak pratila je prodaju novog kolača u svojoj slastičarnici. Podatci o prodaji prikazani su slikovnim dijagramom.

Slikovni dijagram po mjesecima. Jedan smeđi kvadrat predstavlja 120 kolača. Za mjesec siječanj nalazi se 10 kvadrata, za veljaču 9, ožujak 11 kvadrata, travanj 8 i 1/3, svibanj 7 i 1/3 i lipanj 5 i 1/2.

U veljači je prodano približno
kolača.
U travnju je prodano približno
kolača.
U svibnju je prodano približno
kolača.
U lipnju je prodano približno
kolača.

null

Na početku...

Zadatak 1.

Istražimo

Zadatak 2.

Primjer 1.

Kolekcija zadataka #1

Primjer 2.

Zadatak 3.

Kvadrati prirodnih brojeva do 10

Primjer 3.

Kvadriranje

Zadatak 4.

Zadatak 5.

Množenje pomoću modela površine

Primjer 4.

Primjer 5.

Zadatak 6.

Primjer 6.

Primjer 7.

Zadatak 7.

Postupak množenja prirodnih brojeva

Primjer 8.

Zadatak 8.

Primjena množenja prirodnih brojeva

Zadatak 9.

Kolekcija zadataka #2

Procjena

Primjer 9.

Zadatak 10.

Kolekcija zadataka #3

...i na kraju