6.4 Dijeljenje decimalnog broja prirodnim brojem

Što ću naučiti?

dijeliti decimalne brojeve prirodnim brojevima
protumačiti dobiveno rješenje u kontekstu problema
riješiti problemsku situaciju
računati s novcem u problemskoj situaciji

Samostalno učenje

Procjena znanja

Sadržaj jedinice

Na početku...
Dijelimo prirodne brojeve!
1 " title="Dijeljenje decimalnog broja s dekadskim jedinicama većima od $1$ ">Dijeljenje decimalnog broja s dekadskim jedinicama većima od $1$
Dijeljenje decimalnog broja s prirodnim brojem
Primjena dijeljenja
...i na kraju

Na početku...

Martina je pripremila druženje za svojih sedam prijatelja. Nabavila je $24$ kolačića, $16$ bočica vode i $2 kg$ jabuka. Sve zajedno platila je $156 kn .$ Dogovor je bio da se sve, pa i trošak, podijeli na jednake dijelove.

Koliko je svaki od njih dobio kolačića, a koliko bočica vode?

Kolika je masa jabuka koje su dobili?

S kolikim je iznosom u ukupnom računu sudjelovao svaki od njih?

Svaki od njih dobio je $24 : 8 = 3$ kolačića i $16 : 8 = 2$ bočice vode.

Dijeljenjem brojeva $2$ i $8,$ odnosno $156$ i $8$ nećemo dobiti cjelobrojne rezultate.

Zato ostale zadatke moramo rješavati pretvaranjem mjernih jedinica.

Svakome je pripalo $2 kg : 8 = 200 dag : 8 = 25 dag$ jabuka.

Sve zajedno platili su $156 kn : 8 = 15 600 lp : 8 = 1 950 lp = 19.50 kn .$

Je li u prethodnom zadatku moguće masu jabuka i iznos novca odrediti bez pretvaranja mjernih jedinica?

Odgovor je, naravno, potvrdan. U ovoj ćeš jedinici naučiti kako se prirodni i decimalni brojevi dijele prirodnim brojem.

No, za početak, ponovimo!

Kolekcija zadataka #1

Broj koji dijelimo nazivamo

broj kojim dijelimo je

a rezultat dijeljenja nazivamo

null

Ako neki broj dijelimo s brojem

rezultat će biti jednak početnom broju.

null

Dijeljenjem dvaju prirodnih brojeva uvijek dobivamo neki prirodan broj.

null

Koje dijeljenje nije definirano?

0 : 5

0 : 5 = 0

13 : 0

1 : 10

1 : 10 = \frac{1}{10}

13 : 7

13 : 7 = \frac{13}{7}

null

Dijelimo prirodne brojeve!

Primjer 1.

Četiri prijateljice pomogle su susjedi urediti vrt. Susjeda im je za nagradu dala novčanicu od $10$ eura. Kako će pravedno podijeliti nagradu? Koliko će dobiti svaka od njih?

Zaključujemo da je $10 : 4 = 2.5 .$

Dijeljenje 10 : 4 – rukom pisano
10:4=2.5
- 8
20
- 20
= 0 — Dijeljenje 10 : 4 – rukom pisano

Zadatak 1.

Tanja i Ivana imaju $4$ naranče i $3$ čokolade. Kako će ih pravedno podijeliti?

Svaka će dobiti $4 : 2 = 2$ naranče i $3 : 2 = \frac{3}{2} = 1 \frac{1}{2}$ čokolade.

Budući da je $\frac{3}{2} = \frac{15}{10},$ a $\frac{15}{10} = 1.5,$ možemo reći da će svaka dobiti $1.5$ čokolade.

Dakle, vrijedi $3 : 2 = 1.5 .$

Primjer 2.

Koliko je $134 : 8 ?$

S	D	J	d	s		D	J	d	s
$1$	$3$	$4$			$:$ $8$ $=$	$1$	$6 .$	$7$	$5$
	$- 8$
	$5$	$4$
	$- 4$	$8$
		$6$	$0$
		$- 5$	$6$
			$4$	$0$
			$- 4$	$0$
				$0$

Govorimo:

$13$ podijeljeno s $8$ je $1$ ; $1$ puta $8$ je $8$

$13$ minus $8$ je $5$ ; dopisujemo $4$

$54$ podijeljeno s $8$ je $6$ ; $6$ puta $8$ je $48$

$54$ minus $48$ je $6$ ; $6$ cijelih je $60$ desetinki pa dopisujemo $0$ i u količnik pišemo decimalnu točku

$60$ podijeljeno s $8$ je $7$ ; $7$ puta $8$ je $56$

$60$ minus $56$ je $4$ ; $4$ desetinke je $40$ stotinki pa dopisujemo $0$

$40$ podijeljeno s $8$ je $5,$ $5$ puta $8$ je $40$

$40$ minus $40$ je $0.$

$134 : 8 = 16.75$

Primjer 3.

U decimalnom obliku napišimo razlomke:

a) $\frac{14}{5}$

b) $\frac{13}{4},$

c) $\frac{33}{40} .$

a) $\frac{14}{5} = \frac{28}{10} = 2.8$ pa je $\frac{14}{5} = 14 : 5 = 2.8$

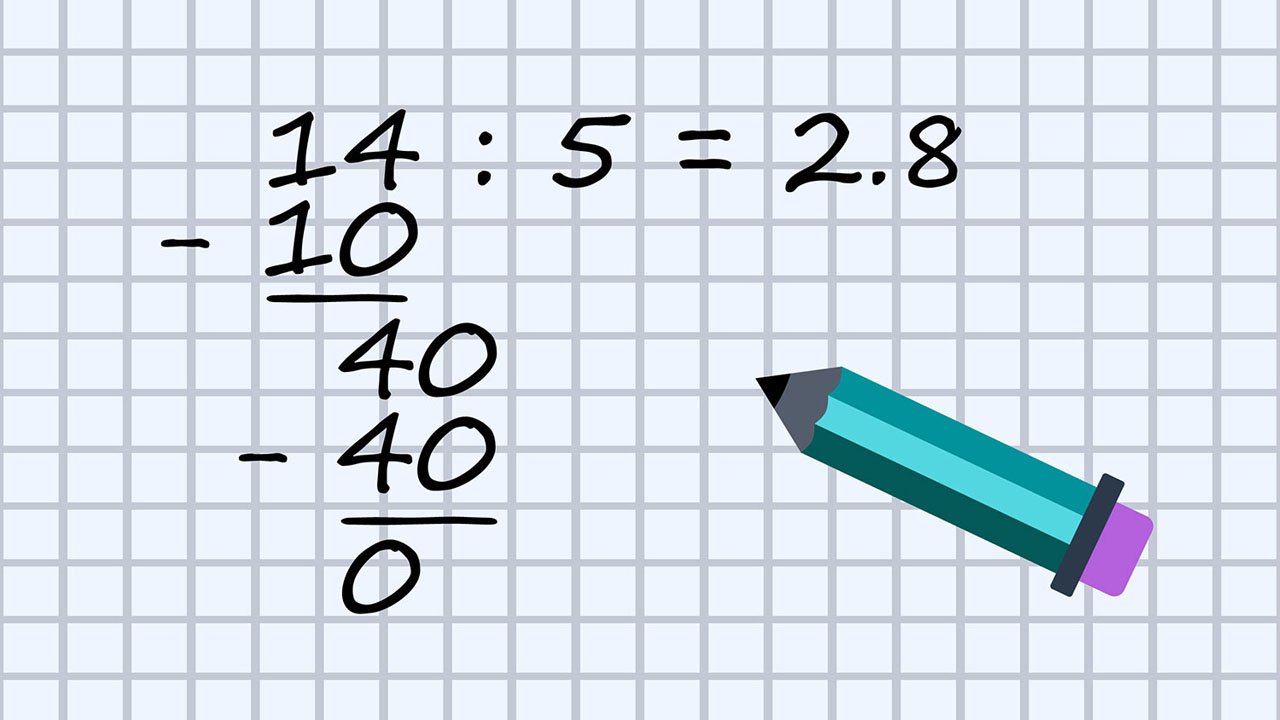
Dijeljenje 14 : 5 – rukom pisano
14:5=2.8
-10
40
- 40
= 0 — Dijeljenje 14 : 5 – rukom pisano

b) $\frac{13}{4} = \frac{325}{100} = 3.25$ pa je $\frac{13}{4} = 13 : 4 = 3.25$

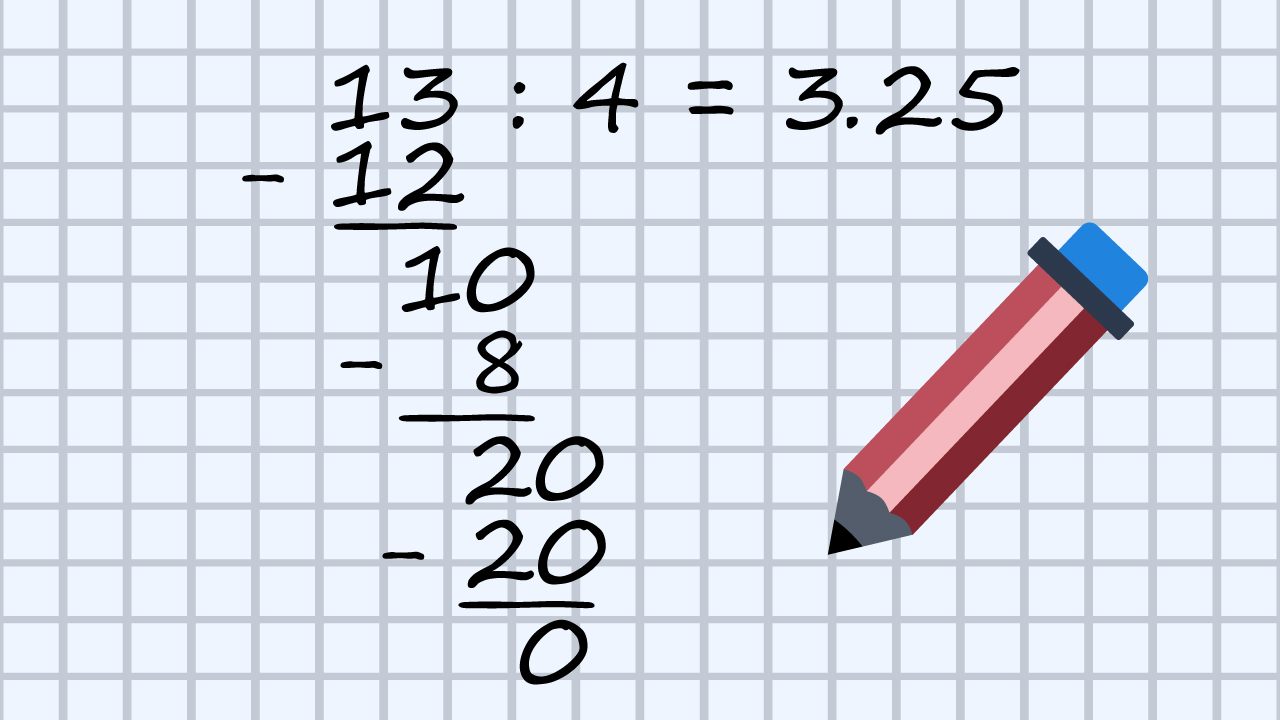
Dijeljenje 13 : 4 – rukom pisano
13:4=3.25
-12
10
- 8
= 20
- 20
= 0 — Dijeljenje 13 : 4 – rukom pisano

c) $\frac{33}{40} = \frac{825}{1 000} = 0.825$ pa je $\frac{33}{40} = 33 : 40 = 0.825$

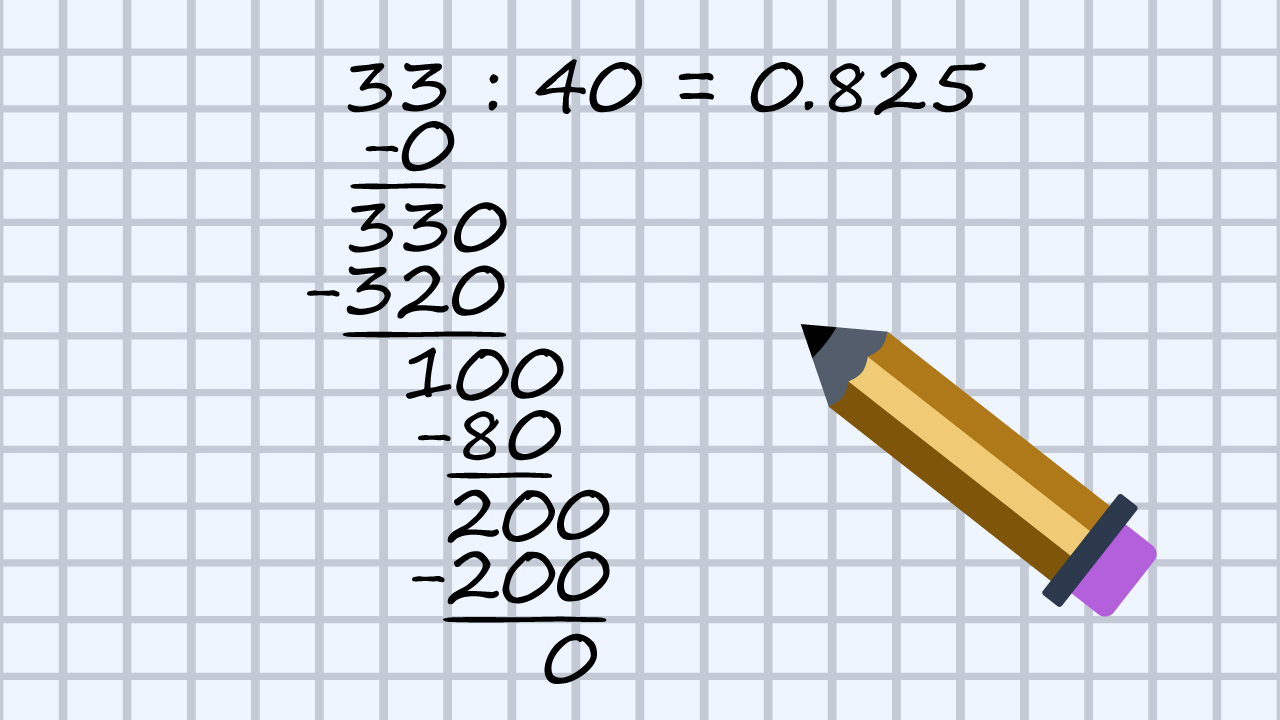
Dijeljenje 33 : 40 – rukom pisano
33:40=0.825
- 0
330
-320
100
-80
200
- 200
0 — Dijeljenje 33 : 40 – rukom pisano

Prirodan broj dijelimo s prirodnim brojem na dobro poznat način, ali kada dođemo do ostatka pripisujemo nulu i stavljamo točku u količniku te nastavljamo s dijeljenjem.

Kolekcija zadataka #2

Podijeli brojnik s nazivnikom pa spoji razlomak s njegovim decimalnim zapisom.

$\frac{5}{8} =$	$0.675$
$\frac{3}{4} =$	$0.6$
$\frac{31}{50} =$	$0.65$
$\frac{27}{40} =$	$0.625$
$\frac{13}{20} =$	$0.75$
$\frac{3}{5} =$	$0.62$

null

Izračunaj i rezultat napiši u obliku decimalnog broja.

4 : 5 =

null

6 : 15 =

null

11 : 25 =

null

17 : 20 =

null

15 : 16 =

null

Mlinar je $27 kg$ brašna rasporedio u $12$ vrećica tako da je svim vrećicama jednaka količina brašna.

U svaku je vrećicu stavio

kilograma

brašna.
Da je istu količinu brašna spakirao u

8

jednakih vrećica, u svaku bi vrećicu stavio

kilograma

brašna.

null

Dijeljenje decimalnog broja s dekadskim jedinicama većima od $1$

Primjer 4.

U tgovini se za $11.3 kn$ prodaje veliki paket papirnatih rupčića. U paketu je $10$ manjih paketića, a u svakome od njih spakirano je po $10$ komada rupčića. Kolika je cijena manjeg paketića rupčića, a kolika jednog rupčića?

Prisjeti se!

$1 kn = 100 lp,$ tj. $1 lp = 0.01 kn$

Problem ćemo riješiti pretvaranjem mjernih jedinica.

Budući da je $11.3 kn = 1130 lp,$ zaključujemo da je cijena jednoga malog paketića

$11.3 kn : 10 = 1130 lp : 10 = 113 lp = 1.13 kn .$

Cijenu jednog rupčića možemo izračunati na dva načina.

I. način

Budući da u manjem paketu ima $10$ rupčića, cijena jednog rupčića je $1.13 kn : 10 = 113 lp : 10 = 11.3 lp = 0.113 kn .$

II. način

U cijelom paketu je $100$ rupčića, pa je cijena jednog rupčića $11.3 kn : 100 = 1130 lp : 100 = 11.3 lp = 0.113 kn .$

Dakle, vrijedi:

$11.3 : 10 = 1.13$

$11.3 : 100 = 0.113$

$1.13 : 10 = 0.113.$

Primjer 5.

U trgovini slažu pakete slatkiša. Masu od $342.6 kg$ treba podijeliti na jednake dijelove.

Koliko bi slatkiša bilo u svakom od $10$ jednakih paketa?

Koliko bi slatkiša bilo u svakom od $100$ jednakih paketa?

Koliko bi slatkiša bilo u svakom od $1 000$ jednakih paketa?

$342.6 : 10 = 34.26$

U svakom od $10$ jednakih paketa bilo bi $34.26 kg$ slatkiša.

$342.6 : 100 = 3.426$

U svakom od $100$ jednakih paketa bilo bi $3.426 kg$ slatkiša.

$342.6 : 1000 = 0.3426$

U svakom od $1 000$ jednakih paketa bilo bi $0.3426 kg$ slatkiša.

Promotri rješenja napisana u tablici.

Količina slatkiša	Broj paketa	Račun	Rješenje
$342.6$	$10$	$342.6 : 10$	$34.26$
$342.6$	$100$	$342.6 : 100$	$3.426$
$342.6$	$1000$	$342.6 : 1 000$	$0.3426$

U prethodnim je primjerima količnik dobiven tako da je decimalna točka u djeljeniku pomaknuta ulijevo za onoliko mjesta koliko dekadska jedinica (djelitelj) ima nula.

Vrijedi i općenito:

Decimalne brojeve dijelimo dekadskim jedinicama tako da decimalnu točku u zadanom broju pomaknemo ulijevo za onoliko mjesta koliko je nula u dekadskoj jedinici.

Kolekcija zadataka #3

Izračunaj.

12.7 : 10 =

null

6.25 : 10 =

null

123.8 : 100 =

null

43.7 : 100 =

null

142.9 : 1000 =

null

45.6 : 1000 =

null

Poveži zadatak i rješenje.

$43.7 : 100 =$
$43.7 : 1 000 =$
$43.7 : 10 =$
$43.7 : 10 000 =$

null

Odaberi odgovarajuću mjernu jedinicu tako da vrijede jednakosti.

$2.5 cm = 0.25$

null

$42 m = 0.042$

null

$31.45 dm = 3.145$

null

$62.5 cm = 0.625$

null

$17.6 mm = 1.76$

null

Površina pravokutnika je $274 {cm}^{2} .$ Spoji moguće parove duljina njegovih stranica.

$10 cm$	$27.4 cm$
$1 000 cm$	$2.74 cm$
$1 cm$	$274 cm$
$100 cm$	$0.274 cm$

null

Dijeljenje decimalnog broja s prirodnim brojem

Primjer 6.

Ivan svakog jutra putem u školu u pekari kupi svoje omiljeno pecivo. Kolika je cijena jednog peciva ako je za pet dana potrošio $22.5 kn ?$

Problem ćemo riješiti pretvaranjem mjernih jedinica.

Budući da je $22.5 kn = 2 250 lp,$ zaključujemo da je cijena jednog peciva

$22.5 kn : 5 = 2250 lp : 5 = 450 lp = 4.50 kn .$

Primjer 7.

Vrtlari u rasadniku žele zemljište površine $2 355.3 m^{2}$ podijeliti na $6$ dijelova jednakih površina. Kolika će biti površina pojedinog dijela?

Problem ćemo riješiti pretvaranjem mjernih jedinica.

Budući da je $2 355.3 m^{2} = 235 530 {dm}^{2},$ zaključujemo da će površina jednog dijela zemljišta biti

$\begin{array}{l} 2 355.3 m^{2} : 6 = 235 530 {dm}^{2} : 6 = 39 255 {dm}^{2} = 392.55 m^{2} \end{array} .$

Primjer 8.

Izračunajmo $13.6 : 4 .$

Budući da ovdje nemamo mogućnost pretvaranja mjernih jedinica, zadatak moramo riješiti nekom drugom metodom.

Decimalan broj dijelimo s prirodnim brojem na sljedeći način:

Cijeli dio djeljenika dijelimo sa zadanim prirodnim brojem. Kad dopisujemo prvu znamenku iza decimalne točke, u količnik pišemo decimalnu točku i nastavljamo dijeliti.

Prisjeti se: Prirodni broj pretvaramo u decimalni tako što iza njega napišemo decimalnu točku i jednu ili nekoliko nula.

Kolekcija zadataka #4

Izračunaj.

15.6 : 2 =

null

21.15 : 3 =

null

6.11 : 13 =

null

50.16 : 24 =

null

Spoji zadatak i rješenje.

$109.35 : 27 =$
$522 : 116 =$
$140.4 : 312 =$
$33.615 : 83 =$

null

Izračunaj pa poredaj zadatke, prema njihovim rješenjima, od najmanjega prema najvećemu.

$66.7 : 23$
$15.9 : 15$
$9.6 : 6$
$28.7 : 41$
$11.02 : 38$

null

Susjed Jura na tržnici prodaje krumpir iz svojega vrta. Krumpir je spakirao u četiri vrećice. U prvoj je bilo $2.96 kg,$ u drugoj $3.17 kg,$ u trećoj $3.25 kg,$ a u četvrtoj $2.8 kg .$ Kolika je prosječna masa krumpira u tim vrećicama?

12.18 kg

6.09 kg

4.06 kg

3.045 kg

3.45 kg

Pomoć:

Ukupna masa krumpira u te četiri vrećice je $12.18 kg .$

null

Primjena dijeljenja

Primjer 9.

Učenici jednoga razrednog odjela pripremaju se na izlet. Ukupni troškovi izleta su $5 720 kn$ i dijele se na $25$ učenika. Koliko novca treba uplatiti svaki učenik?

Ukupni se troškovi dijele na $25$ jednakih dijelova pa svaki učenik treba uplatiti iznos od $5 720 kn : 25 = 228.8 kn .$

Zadatak 2.

Matko s roditeljima putuje na ljetovanje. Vozeći stalnom brzinom, automobilom su za $5$ sati prešli $362 km .$ Koliko su kilometara prelazili u jednom satu?

Prosječnu brzinu odredit ćemo tako da podijelimo prijeđeni put s vremenom putovanja.

Dakle, u svakom satu prelazili su prosječno $362 km : 5 = 72.4 km .$

Kolekcija zadataka #5

Marija je kupila

4

jednake čokoladice. Ukupno ih je platila

12.80

kuna. Cijena jedne čokoladice je

kn .

null

Baka je napravila je

19.5

litara sirupa od mente kojim je napunila

26

jednakih boca boca. U svaku je bocu nalila

litara

sirupa. Da je isti sirup spremila u bočice od

3 dl,

napunila bi

bočica.

Pomoć:

$19.5 l = 195 dl$

null

Ivo je kupio knjigu i $3$ jednake bilježnice. Cijena kupljene knjige je $49.50 kn,$ a račun je platio novčanicom od $100 kn .$ Prodavač mu je uzvratio $12.25 kn .$

Kolika je cijena jedne bilježnice?

38.25 kn

29.25 kn

16.5 kn

12.75 kn

Nijedan od navedenih iznosa.

null

Postupak:

Ivo je ukupno potrošio $100 - 12.25 = 87.75 kn .$ Od tog je iznosa na bilježnice potrošio $87.75 - 49.50 = 38.25 kn .$ Dakle cijena jedne bilježnice iznosi $38.25 : 3 = 12.75 kn .$

Kutak za znatiželjne

Za kraj malo statistike! Pri rješavanju zadataka možeš se poslužiti džepnim računalom.

U tablici su navedene količine oborina po mjesecima u 2018. godini za Varaždin i Rijeku. (Količinu oborina mjerimo u litrama po četvornome metru.)

	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.
Varaždin	$32.4$	$56.0$	$20.1$	$32.5$	$66.7$	$84.5$	$54.0$	$42.2$	$242.1$	$69.0$	$104.9$	$88.0$
Rijeka	$95.6$	$336.8$	$53.5$	$101.8$	$77.1$	$63.8$	$88.1$	$47.3$	$249.2$	$153.9$	$204.6$	$263.6$

Promotri tablicu, izračunaj i dopuni rečenice:

Ukupna količina oborina u Varaždinu bila je

a u Rijeci

litre

po četvornome metru.
Prosječna količina oborina tijekom svih 12 mjeseci, zaokružena na jednu decimalu, u Varaždinu bila je

a u Rijeci

litara

po četvornome metru.

null

Koristeći se podatcima iz prethodne tablice i izračunanim prosjecima, odgovori na pitanja.

U kojim je mjesecima u Varaždinu palo više kiše nego u Rijeci?

u svibnju

u lipnju

u srpnju

u kolovozu

null

U kojem je mjesecu količina oborina u Rijeci bila najbliža prosjeku?

u siječnju

u travnju

u rujnu

u listopadu

null

...i na kraju

Riješite postavljene zadatke i obojite sliku!

Na početku...

Kolekcija zadataka #1

Dijelimo prirodne brojeve!

Primjer 1.

Zadatak 1.

Primjer 2.

Primjer 3.

Kolekcija zadataka #2

Dijeljenje decimalnog broja s dekadskim jedinicama većima od 1

Primjer 4.

Primjer 5.

Kolekcija zadataka #3

Dijeljenje decimalnog broja s prirodnim brojem

Primjer 6.

Primjer 7.

Primjer 8.

Kolekcija zadataka #4

Primjena dijeljenja

Primjer 9.

Zadatak 2.

Kolekcija zadataka #5

Kutak za znatiželjne

...i na kraju

Dijeljenje decimalnog broja s dekadskim jedinicama većima od $1$