Matematika 5 - 7.4 Volumen kocke i kvadra

Na početku...

Petra i Matko slažu kockice. Odlučili su, koristeći samo 3 jednake kockice, složiti što više različitih građevina. Pogledajte što su sve složili!

Građevine od 3 kockice

Zadatak 1.

Jesu li sve ove građevine zaista međusobno različite?

Neke od građevina su zapravo jednake, samo su postavljene drukčije, tj. vidljive su s različitih strana. Primjerice, jednake su građevine na slici:

Građevine od 3 kockice - jednake.
1. Polegnute u jednoj liniji (dvije)
2. U obliku slova L, polegnute (3)
3. U obliku slova L, uspravne (3) — Građevine od 3 kockice - jednake

Zadatak 2.

Što je zajedničko svim ovim građevinama?

Sve ove građevine zauzimaju jednak prostor, 3 jedinice (3 jedinične kocke). Kažemo da sve ove građevine imaju isti volumen.

Volumen (obujam)

Sva tijela zauzimaju određeni prostor. Mjera zauzetog prostora naziva se volumen ili obujam tijela.

Geometrijska tijela, valjak, kvadar, kocka, stožac i piramida. — Geometrijska tijela

Obujam ili volumen tijela je broj jediničnih kocaka koje potpuno popunjavaju tijelo.

Osnovna mjerna jedinca za volumen je kubni metar ( $1 m^{3}$ ).

Kubni metar je volumen kocke kojoj je brid duljine $1$ metar.

Uz osnovne mjerne jedinice, postoje veće i manje jedinice za mjerenje volumena. Od većih spominjemo kubni kilometar (oznaka ${km}^{3}$ ), a od manjih kubmi decimetar (oznaka ${dm}^{3}$ ), kubni centimetar (oznaka ${cm}^{3}$ ) i kubni milimetar (oznaka ${mm}^{3}$ ).

U sljedećoj su tablici navedene veze među mjernim jedinicama za volumen.

$1 m^{3} = 1 000 {dm}^{3}$

$1 m^{3} = 1 000 000 {cm}^{3}$

$1 m^{3} = 1 000 000 000 {mm}^{3}$

$1 {dm}^{3} = 1 000 {cm}^{3}$

$1 {dm}^{3} = 1 000 000 {mm}^{3}$

$1 {cm}^{3} = 1 000 {mm}^{3}$

$1 {km}^{3} = 1 000 000 000 m^{3}$

Za volumen tekućine kao mjernu jedinicu najčešće upotrebljavamo litru, te manje mjerne jedinice ‒ decilitar, centilitar i mililitar.

Prisjeti se $1 l = 1 {dm}^{3}$

Primjer 1.

Preračunajmo iz većih u manje mjerne jedinice za volumen.

$13 m^{3}$ u kubne decimetre

$2.7 {dm}^{3}$ u kubne centimetre

$0.6 {dm}^{3}$ u kubne milimetre

$15.5 {cm}^{3}$ u kubne milimetre

$0.25 {km}^{3}$ u kubne metre

$13 m^{3} = 13 \cdot 1000 = 13 000 {dm}^{3}$

$2.7 {dm}^{3} = 2.7 \cdot 1000 = 2 700 {cm}^{3}$

$0.6 {dm}^{3} = 0.6 \cdot 1 000 000 = 600 000 {mm}^{3}$

$15.5 {cm}^{3} = 15.5 \cdot 1000 = 15 500 {mm}^{3}$

$0.25 {km}^{3} = 0.25 \cdot 1 000 000 = 250 000 m^{3}$

Primjer 2.

Preračunajmo iz manjih u veće mjerne jedinice za volumen.

$472 {cm}^{3}$ u kubne decimetre

$6 250 {dm}^{3}$ u kubne metre

$3 425 {mm}^{3}$ u kubne decimetre

$469 750 m^{3}$ u kubne kilometre

$54 258 700 {mm}^{3}$ u kubne decimetre

$472 {cm}^{3} = 472 : 1 000 = 0.472 {dm}^{3}$

$6 250 {dm}^{3} = 6 250 : 1 000 = 6.25 m^{3}$

$3 425 {mm}^{3} = 3 245 : 1 000 000 = 0.003425 {dm}^{3}$

$469 750 m^{3} = 469 750 : 1 000 000 000 = 0.00046975 {km}^{3}$

$54 258 700 {mm}^{3} = 54 258 700 : 1 000 000 = 54.2587 {dm}^{3}$

Zadatak 3.

Odaberi ispravne jednakosti.

$2.7 {cm}^{3} = 27 {mm}^{3}$

$2.7 {mm}^{3} = 0.270 {cm}^{3}$

$2.7 {cm}^{3} = 2 700 {mm}^{3}$

$2.7 {cm}^{3} = 0.0027 {mm}^{3}$

null

Zadatak 4.

Dopuni jednakosti.

$4.5 {cm}^{3} =$

${mm}^{3} .$

null

$0.4 {cm}^{3} =$

${dm}^{3} .$

null

$4 500 {cm}^{3} =$

${dm}^{3} .$

null

Volumen kocke

Kocka je geometrijsko tijelo omeđeno sa šest sukladnih (jednakih) kvadrata koje nazivamo stranama kocke.

Kocka, uz šest strana, ima $8$ vrhova i $12$ bridova.

Duljine svih bridova kocke međusobno su jednake.

Istražimo

Istraži kako volumen kocke ovisi o duljini njezina brida

Volumen ili obujam kocke jednak je broju jediničnih kocaka koje ju potpuno ispunjavaju.

Volumen kocke s bridom duljine $1 cm$ iznosi $1 {cm}^{3} .$

Kocke s bridom 1, 2 i 3. Prva kocka je najmanja, druga je malo veća dok je treća najveća. — Kocke s bridom 1, 2 i 3

Volumen kocke s bridom duljine $a$ računamo prema formuli $V = a \cdot a \cdot a,$ što kraće zapisujemo $V = a^{3} .$

Primjer 3.

Izračunajmo volumen kocke s bridom duljine:

a) $a = 4 cm,$

b) $a = 0.7 dm .$

a) Uvrštavanjem zadanog podatka u izraz $V = a^{3} = a \cdot a \cdot a$ $,$ dobivamo $V = 4^{3} = 4 \cdot 4 \cdot 4,$ tj. $V = 64 {cm}^{3} .$

b) Uvrštavanjem zadanog podatka u izraz $V = a^{3} = a \cdot a \cdot a$ $,$ dobivamo $V = {0.7}^{3} = 0.7 \cdot 0.7 \cdot 0.7,$ tj. $V = 0.343 {dm}^{3} .$

Zadatak 5.

Koliki je volumen kocke s bridom duljine $a = 1 dm ?$

$10 {cm}^{3}$

$100 {cm}^{3}$

$1 000 {cm}^{3}$

$10 000 {cm}^{3}$

null

Zadatak 6.

U kutiju oblika kocke s bridom duljine

$4 dm$ slažu se manje kocke, s bridom duljine

$5 cm .$ Na dno te kutije možemo složiti najviše

manje

kutije. U veliku kutiju stane ukupno

malih

kutija.
Ako je u veliku kutiju već složeno

$145$ malih kutija, do polovine ukupnog broja treba dodati još

malih

kutija.

null

Volumen kvadra

Kvadar je geometrijsko tijelo omeđeno s tri para međusobno sukladnih (jednakih) pravokutnika koje nazivamo stranama kvadra.

Kvadar, uz šest strana, ima $8$ vrhova i $12$ bridova.

Istražimo

Istraži kako volumen kvadra ovisi o duljinama njegovih bridova. Jedinične kockice "primi" za crvenu točku i posloži ih jednu do druge (bez preklapanja i praznog prostora) dok ne "napuniš" kvadar.

Volumen ili obujam kvadra jednak je broju jediničnih kocaka koje ga potpuno ispunjavaju.

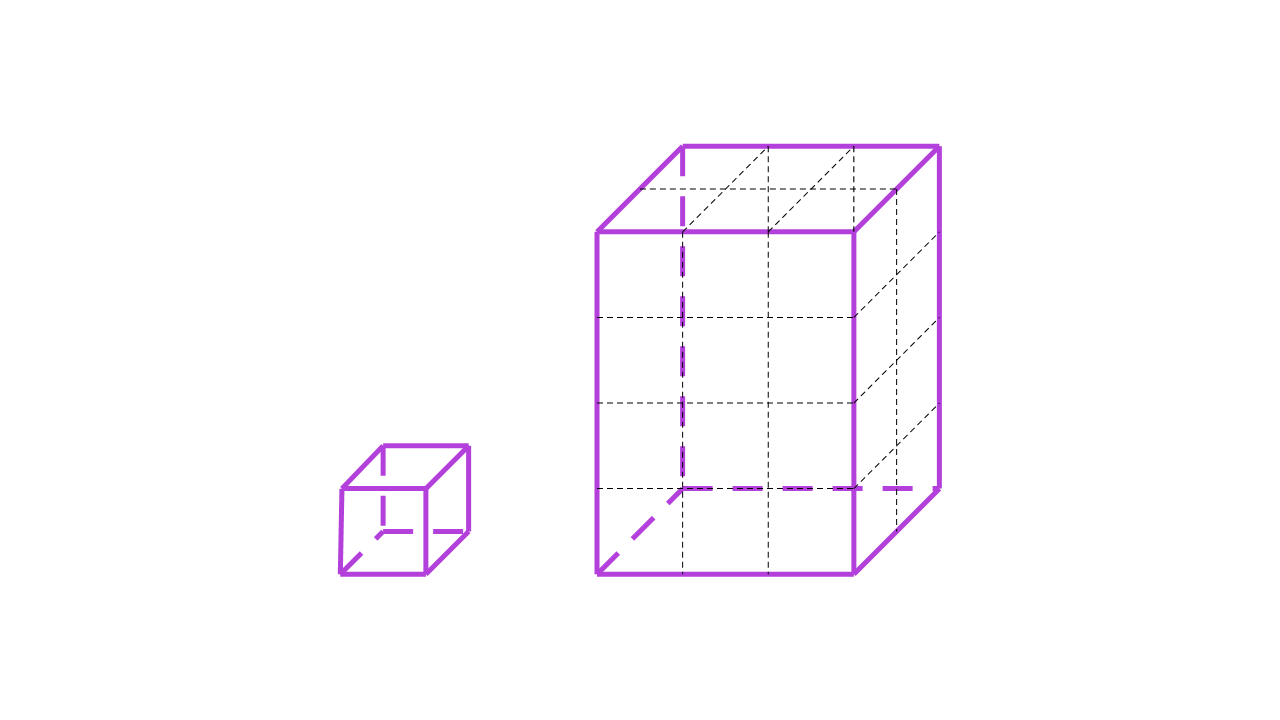
jedinična kocka i kvadar 3 x 2 x 4 — Jedinična kocka i kvadar 3 x 2 x 4

Volumen kvadra s bridovima duljine $a,$ $b$ i $c$ računamo prema formuli $V = a \cdot b \cdot c .$ Dakle, volumen kvadra jednak je umnošku duljina triju bridova koji se sastaju u istom vrhu.

Primjer 4.

Izračunajmo volumen kvadra s bridovima duljine $a = 4 cm,$ $b = 6 cm,$ $c = 1 dm .$

Nakon ujednačavanja mjernih jedinica ( $a = 4 cm,$ $b = 6 cm,$ $c = 10 cm$ ), zadane podatke uvrštavamo u izraz (formulu) $V = a \cdot b \cdot c,$

Uvrštavanjem nalazimo da je $V = 4 \cdot 6 \cdot 10,$ tj. da je $V = 240 {cm}^{3} .$

Primjer 5.

Volumen nekog kvadra iznosi $35.2 {dm}^{3},$ a duljine njegovih bridova su $a = 32 cm$ i $b = 2.5 dm .$ Kolika je duljina brida $c ?$

Uvrstimo li zadane podatke (nakon ujednačavanja mjernih jedinica) u izraz za računanje volumena kvadra $V = a \cdot b \cdot c,$ dobit ćemo:

$35 200 = 32 \cdot 25 \cdot c,$ odnosno $32 500 = 800 \cdot c .$

Rješavanjem ove jednadžbe (sjeti se: nepoznati faktor nalazimo tako da umnožak podijelimo poznatim faktorom) dobivamo da je $c = 35 200 : 800 = 44 cm .$

Zadatak 7.

U akvarij u obliku kvadra s bridovima duljine $a = 40 cm,$ $b = 3 dm$ i $c = 2.5 dm$ uliveno je $18 l$ vode. Do koje se visine podigla razina vode u akvariju? Koliko bi litara vode još stalo do vrha tog akvarija? (Napomena: $c$ je visina akvarija).

Volumen tog akvarija je $V = 40 \cdot 30 \cdot 25 = 30 000 {cm}^{3},$ tj. u njega stane $30 l$ vode.

Površina dna tog akvarija je $40 \cdot 30 = 1 200 {cm}^{2}$ pa uvrštavanjem u formulu za volumen kvadra $V = a \cdot b \cdot c$ dobivamo da su visina vode $h$ i volumen ulivene vode povezani jednadžbom $18 000 = 1 200 \cdot h .$ Rješavanjem te jednadžbe dobivamo da je visina vode u akvariju $h = 18 000 : 1 200 = 15 cm .$

Količinu vode koja bi još stala u akvarij možemo izračunati na dva načina.

I. način ‒ Ako je volumen akvarija $30 l,$ a u njemu je već $18 l$ vode, u akvarij stane još $12 l$ vode.

II. način ‒ Ako je akvarij pun do visine od $15 cm,$ do ruba akvarija ima još $25 - 15 = 10 cm .$ Volumen vode koja još stane u akvarij jednak je $1 200 \cdot 10 = 12 000 {cm}^{3} = 12 {dm}^{3} = 12 l .$

Kolekcija zadataka #1

Zadan je kvadar s bridovima duljine $a,$ $b,$ $c .$ Spoji duljine bridova i volumen kvadra.

$a = 8 cm,$ $b = 1.2 dm,$ $c = 2.5 cm$	$V = 189 {cm}^{3}$
$a = 7 cm,$ $b = 0.6 dm,$ $c = 4.5 cm$	$V = 240 {cm}^{3}$
$a = 3 cm,$ $b = 0.3 dm,$ $c = 1.4 dm$	$V = 126 {cm}^{3}$
$a = 1.3 dm,$ $b = 0.03 m,$ $c = 5 cm$	$V = 195 {cm}^{3}$

null

Koji kvadar s bridovima duljine $a,$ $b,$ $c$ ima najmanji volumen?

$a = 4 cm,$

$b = 7.5 cm,$

$c = 83 mm$

$a = 5.6 cm,$

$b = 0.95 dm,$

$c = 4.5 cm$

$a = 55 mm,$

$b = 8.2 cm,$

$c = 68 mm$

$a = 4.8 cm,$

$b = 85 mm,$

$c = 0.8 dm$

null

Dva kvadra imaju jednake volumene. Duljine bridova prvog kvadra su

$12 cm,$

$2.5 m,$

$0.32 dm .$ Duljine dvaju bridova drugog kvadra su

$24 cm$ i

$4 dm .$
Duljina trećeg brida drugog kvadra je

$cm .$

Pomoć:

Izračunaj volumen prvog kvadra (pri čemu vodi računa da su sve duljine stranica izražene u istim mjernim jedinicama). To je ujedno i volumen drugog kvadra. Duljinu nepoznate stranice drugog kvadra možeš izračunati tako da volumen podijeliš umnoškom duljina dviju poznatih stranica kvadra.

null

Posuda volumena $12 l$ napunjena je vodom. Vodu treba preliti u dvije posude. Prvo treba vodom napuniti posudu u obliku kocke s bridom duljine $20 cm,$ a ostatak treba preliti u posudu u obliku kvadra s bridovima duljine $a = 25 cm,$ $b = 16 cm$ i $c = 35 cm .$ Do koje će visine biti napunjena druga posuda?

(Napomena: $c$ je visina posude).

$5 cm$

$10 cm$

$20 cm$

Voda neće stati u drugu posudu.

Pomoć:

$12 l = 12 {dm}^{3} = 12 000 {cm}^{3}$

Postupak:

$12 l = 12 {dm}^{3} = 12 000 {cm}^{3}$

Volumen kocke je $20 \cdot 20 \cdot 20 = 8 000 {cm}^{3},$ pa za drugu posudu ostaje $12 000 - 8 000 = 4 000 {cm}^{3}$ vode.

Površina dna druge posude je $25 \cdot 16 = 400 {cm}^{2} .$

Da bismo odredili visinu vode u drugoj posudi, trebamo volumen vode ( $4000 {cm}^{3}$ ) podijeliti s površinom dna posude ( $400 {cm}^{2}$ ).

$27 000 {mm}^{3} =$	$2.7 {dm}^{3}$
$2.7 {cm}^{3} =$	$270 000 {mm}^{3}$
$0.27 {dm}^{3} =$	$2 700 {mm}^{3}$
$2 700 {cm}^{3} =$	$0.027 {dm}^{3}$

7.4 Volumen kocke i kvadra