Na početku...

U animaciji su prikazani brojevi u zapisu koji se naziva decimalni. Više o tom zapisu te kako prelaziti iz decimalnog zapisa u razlomački naučit ćeš u ovoj jedinici.

Zanimljivost

Naš brojevni sustav naziva se dekadski brojevni sustav jer mu je baza broj deset.

Dekadski ili decimalni razlomak je razlomak kojemu je u nazivniku dekadska jedinica. Primjeri decimalnih razlomaka uključuju brojeve $\frac{7}{10},$ $\frac{27}{100},$ $\frac{111}{1 000}$ itd.

Svaki decimalni/dekadski razlomak može se napisati na jednostavniji način – kao decimalni broj.

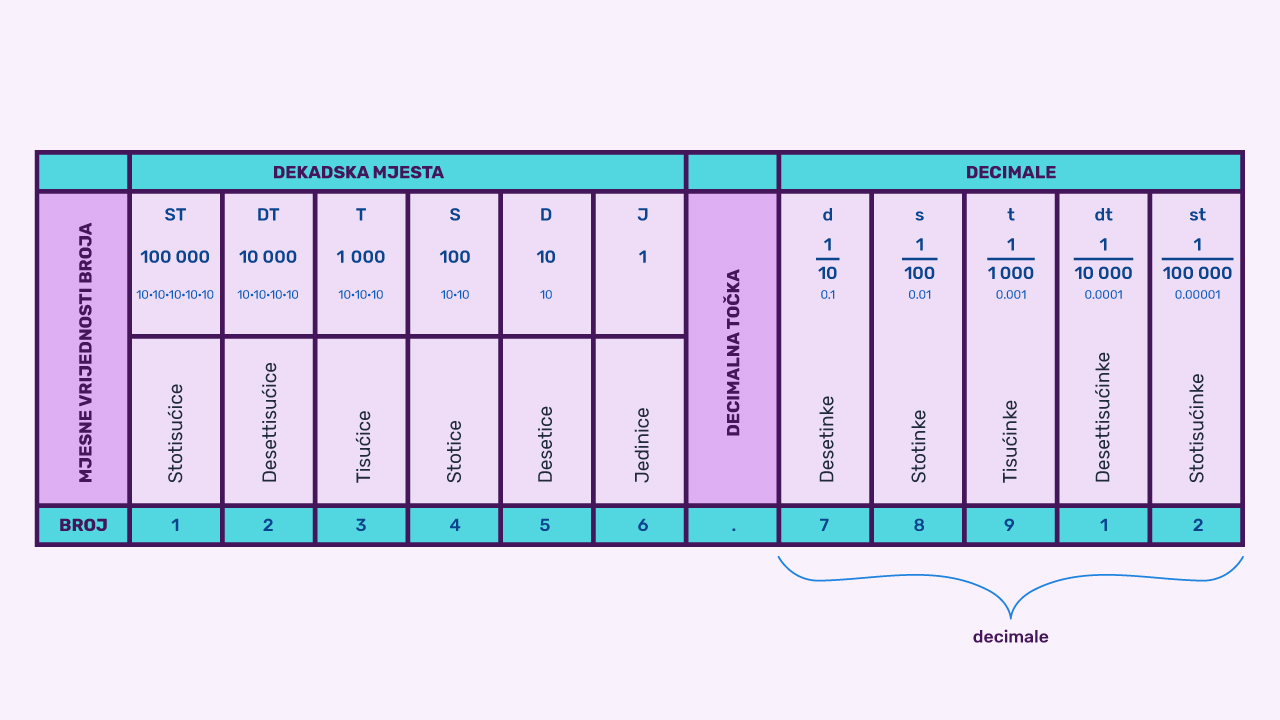
Decimalni broj sastoji se od dvaju dijelova, cijelog i decimalnog, međusobno odvojenih decimalnom točkom.

Prvu znamenku desno od decimalne točke zovemo desetinka, drugu stotinka, treću tisućinka i tako redom. Te znamenke jednim imenom nazivamo decimale.

Zanimljivost

Dekadski razlomci javljaju se u djelima matematičara u periodu od 14. do 16. stoljeća. Neki od njih ističu da se do dekadskih razlomaka može doći "tako da se jedinica podijeli na deset jednakih dijelova, a onda se svaki taj dio dalje dijeli na deset jednakih dijelova itd.”.

Iz ovoga perioda treba istaknuti nizozemskog matematičara i inženjera Simona Stevina koji je u djelu Desetka (1585.) uveo dekadske razlomke i izložio koliko su oni u primjenama praktičniji od drugih razlomaka. Ovaj rad predstavljao je temelje za ujednačavanje sustava mjera na dekadskoj osnovi.

Približno 150 godina prije ove Stevinove knjige arapski matematičar al-Kashi u djelu Ključ aritmetike izložio je učenje o decimalnim brojevima. Ova knjiga dugo je bila nepoznata u Europi te Stevin vjerojatno nije mogao znati za nju.

Uoči, pri nazivu mjesnih jedinica desno od decimalne točke dodajemo nastavak ''-inka''

Tablica mjesnih vrijednosti. Prva red tablice podijeljne je na dekadska mjesta i na decimale. Dekadska mjesta podijeljena su na mjesne vrijednosti broja (stotisućice, desettisućice, tisućice, stotice, desetice i jedinice). Ispod tih vrijednosti nalaze se brojevi 1, 2, 3, 4, 5 i 6. Prvi red (dekadska mjesta i decimale) odvodjen je stupcem decimalna točka. Decimale su podijeljene na desetinke, stotinke, tisućinke, desettisućinke i stotisućinke. Ispod tih stupaca su brojevi 7, 8, 9, 1 i 2 koji su oznaćeni kao decimale. — Tablica mjesnih vrijednosti

Čitanje decimalnih brojeva

Istražimo

Prouči kako se čitaju decimalni brojevi.

a) $3.8$ čita se tri cijela i osam desetinki

b) $0.31$ čita se nula cijelih i trideset jedna stotinka

c) $1.234$ čita se jedno cijelo dvjesto trideset četiri tisućinke

d) $0.07$ čita se nula cijelih sedam stotinki

e) $2.0001$ čita se dva cijela jedna desettisućinka

Kolekcija zadataka #1

Poveži odgovarajuće parove.

$0.0029$	dva cijela devet desetinki
$2.9$	nula cijelih dvadeset devet stotinki
$0.029$	nula cijelih dvadeset devet desettisućinki
$0.29$	nula cijelih dvadeset devet tisućinki

null

Broj $3.004$ čita se tri cijela četiri
.
Broj $2.0017$ čita se dva cijela sedamnaest
.
Broj $5.3$ čita se pet cijelih tri
.

null

Broj $4.07$ čita se četiri cijela sedam
.
Broj $3.12$ čita se tri cijela dvanaest
.
Broj $0.125$ čita se nula cijelih sto dvadeset i pet
.

null

Razlomački i decimalni zapis broja

Istražimo

Promotri tablicu.

Razlomački zapis $\frac{7}{10}$ $\frac{17}{10}$ $\frac{345}{10}$ $\frac{7}{100}$ $\frac{11}{100}$ $\frac{121}{100}$ $\frac{3}{1000}$ $\frac{27}{1000}$ $\frac{12345}{10000}$

Decimalni broj $0.7$ $1.7$ $34.5$ $0.07$ $0.11$ $1.21$ $0.003$ $0.027$ $1.2345$

Primjećuješ li pravilnost? Koliko decimala ima decimalni zapis razlomka kojemu je nazivnik broj $10 ?$ Koliko decimala ima decimalni zapis razlomka kojemu je nazivnik $100 ?$ A $1 000 ?$ A $10 000 ?$

Pri uočavanju pravilnosti pomoći će ti i sljedeći aplet.

Decimalni (dekadski) razlomak u svom decimalnom zapisu ima onoliko decimala koliko nazivnik tog razlomka ima znamenaka $0 .$

Zadatak 1.

Poveži decimalni razlomak s njemu odgovarajućim decimalnim brojem.

$\frac{17}{100}$	$0.0017$
$\frac{17}{10 000}$	$0.017$
$\frac{17}{1 000}$	$1.7$
$\frac{17}{10}$	$0.17$

null

Zadatak 2.

Dopuni.

$\frac{1 234}{100} =$
$\frac{1 234}{10} =$
$\frac{1 234}{10 000} =$
$\frac{1 234}{1 000} =$

null

Primjer 1.

Zapišimo u obliku razlomka:

a) $1.2$

b) $7.239$

c) $103.4 .$

a) $1.2 = \frac{12}{10}$

b) $7.239 = \frac{7 239}{1 000}$

c) $103.4 = \frac{1 034}{10}$

Decimalni broj pišemo u obliku decimalnog razlomka tako da u brojnik napišemo broj bez decimalne točke, a u nazivnik dekadsku jedinicu s onoliko nula koliko početni broj ima decimala.

Primjer 2.

Dopunimo decimalnim brojem.

a) $54 mm$ je koliko $cm$

b) $1 234 lp$ je koliko $kn$

c) $56 {cm}^{2}$ je koliko ${dm}^{2}$

d) $43 g$ je koliko $kg$

a) $54 mm = 5 cm 4 mm = 5 \frac{4}{10} cm = 5.4 cm$

b) $1 234 lp = 12 kn 34 lp = 12 \frac{34}{100} kn = 1 2.34 kn$

c) $56 {cm}^{2} = 0.56 {dm}^{2}$

d) $43 g = 0.043 kg$

Zadatak 3.

Dopuni.

$3 dm =$

$m$
$12 cm =$

$m$
$117 cm =$

$m$
$39 mm =$

$m$

null

Postotci i promili

Zadatak 4.

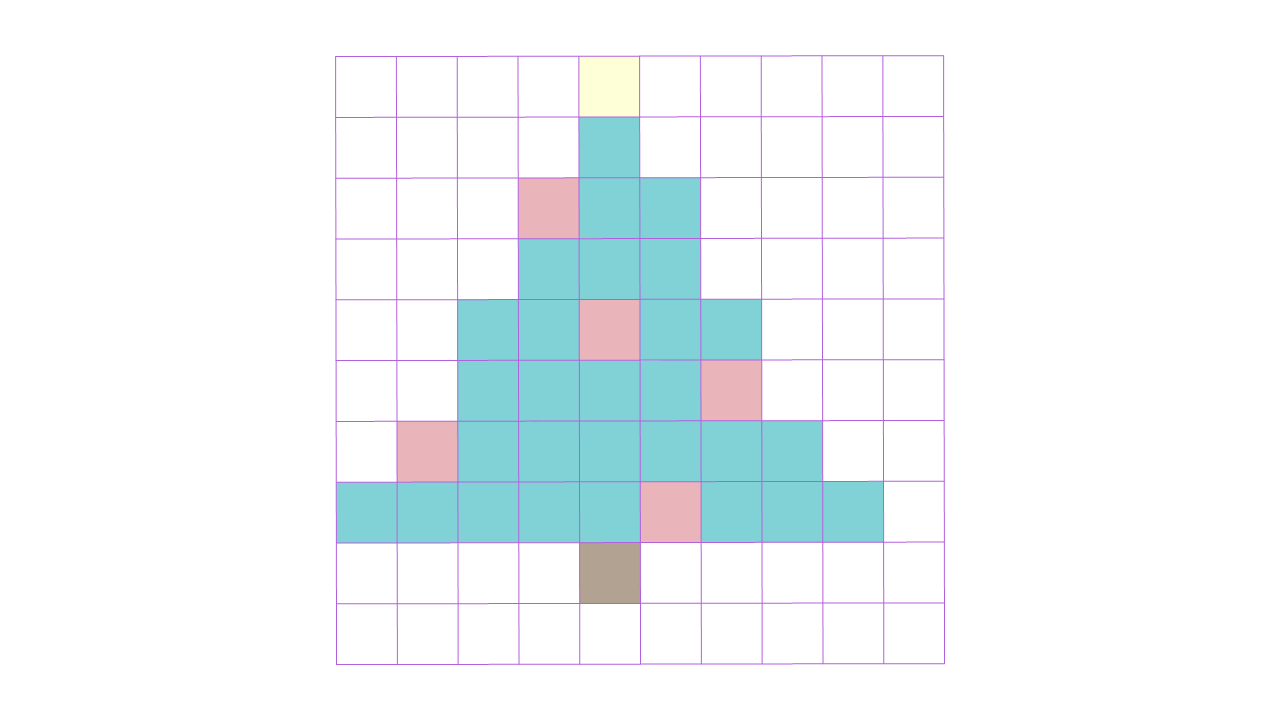
U mreži od $100$ kvadratića prikazan je crtež božićnog drvca. Iskaži udio svake boje razlomkom i decimalnim brojem.

Svaki kvadratić predstavlja $\frac{1}{100},$ tj. $0.01$ mreže.

Zelenom bojom obojeno je $\frac{28}{100},$ tj. $0.28$ mreže.

Crvenom bojom obojeno je $\frac{5}{100},$ tj. $0.05$ mreže.

Žutom bojom obojena je $\frac{1}{100},$ tj. $0.01$ mreže.

Smeđom bojom obojena je $\frac{1}{100},$ tj. $0.01$ mreže.

U prethodnom zadatku udio kvadratića obojenih pojedinom bojom iskazivali smo razlomkom s nazivnikom $100$ i decimalnim brojem. Svaki razlomak s nazivnikom $100$ može se zapisati u obliku postotka.

Umjesto zelenom bojom obojeno je $\frac{28}{100},$ tj. $0.28$ mreže, možemo reći zelenom bojom obojeno je $28 %$ mreže (čitamo $28$ posto).

Postotak

Postotak je razlomak s nazivnikom $100 .$ Oznaka za postotak je $% .$ Oznaka $%$ čita se posto.

$1 % = \frac{1}{100}$

Primjer 3.

Postotak je razlomak s nazivnikom $100$ te možemo pisati:

$3 % = \frac{3}{100} = 0.03$

$15 % = \frac{15}{100} = 0.15$

$100 % = \frac{100}{100} = 1$

$150 % = \frac{150}{100} = 1.5$

Postotci na računu iz dućana

Grafikon omjera vode i kopna na Zemlji

Natpis "Velika rasprodaja"

Novinski članak

Istražimo

Pretvaranja iz jednog zapisa u drugi možeš dodatno proučiti pomoću sljedećeg apleta.

Primjer 4.

Cijena jakne prije sniženja iznosila je $400 kn .$ Jakna se prodaje na sniženju od $30 % .$ Za koliko je kuna snižena cijena jakne?

Potrebno je izračunati $30 %$ od $400 .$ U razlomačkom zapisu $30 % = \frac{30}{100} .$

$\frac{30}{100}$ od $400$ iznosi $(400 : 100) \cdot 30 = 4 \cdot 30 = 120 .$

Cijena jakne snižena je za $120 kn .$

Cijena šestara za ploču iznosi

200 kn .

Na tu cijenu obračunava se PDV (porez na dodanu vrijednost) u iznosu od

25 %

cijene. Ukupna cijena koju treba platiti za šestar iznosi

kn .

null

Postupak:

Cijenu od $200 kn$ treba uvećati za PDV, tj. $25 %$ od $200 kn .$

Tekst o dozvoljenoj količini alkohola prilikom vožnje.

Saliniteti mora

Stopa prirodnog prirasta

Zanimljivost

Riječ promil dolazi iz latinskog pro mille što znači kroz tisuću, na tisuću. Hrvatski naziv za promil glasi potisućak.

Promil

Promil je razlomak s nazivnikom $1 000 .$ Oznaka za promil je $‰ .$

$1 ‰ = \frac{1}{1 000}$

Primjer 5.

Promil je razlomak s nazivnikom $1 000$ te možemo pisati:

$7 ‰ = \frac{7}{1 000} = 0.007$

$43 ‰ = \frac{43}{1 000} = 0.043$

$100 ‰ = \frac{100}{1 000} = 0.1 .$

Zadatak 5.

Poveži tri odgovarajuće kartice.

Povećaj interaktivni prikaz

Kolekcija zadataka #2

Farmaceutska kompanija testira umjetnu pužnicu. Tijekom istraživanja pokazalo se da

3

1 000

ljudi nakon ugradnje umjetne pužnice osjeti mučninu. Nakon ugradnje umjetne pužnice

promila

korisnika osjeti mučninu.

null

Stopa nataliteta u Republici Hrvatskoj u 2018. godini iznosila je

9 ‰ .

To znači da je devetero djece rođeno na svakih

stanovnika

Republike Hrvatske.

null

1 000

grama vode iz Jonskog mora nalazi se

35

grama soli. Salinitet Jonskog mora iznosi

promila.

null

Beskonačni decimalni zapis

Primjer 6.

Petar zna da razlomci predstavljaju računsku operaciju dijeljenja.

Koristeći se računalom, pretvorio je razlomak $\frac{1}{3}$ u njemu odgovarajući decimalni zapis.

Dijeljenjem broja $1$ s brojem $3$ na zaslonu računala ispisalo se $0.33333333333.. .$

Petar zna da tri točke na kraju broja znače da će se decimala $3$ nastaviti ponavljati u beskonačnost, no pita se kako zapisati takav broj. Znaš li ti?

Broj $0.33333333333.. .$ primjer je beskonačnog decimalnog zapisa. S obzirom na to da se znamenka $3$ ponavlja, broj kraće možemo zapisati $0.33333333333.. . = 0 . \bar{3} = 0 . \dot{3} .$

Ako se u beskonačnom decimalnom zapisu ponavlja jedna znamenka, iznad nje crtamo točkicu ili crticu. Ako se ponavlja više znamenaka, crtamo točkicu iznad prve i iznad zadnje znamenke koja se ponavlja ili crticu iznad svih znamenaka koje se ponavljaju.

Zanimljivost

Broj u svom decimalnom zapisu može biti beskonačan. Ako se znamenke toga broja periodički ponavljaju, taj se broj naziva beskonačni periodički decimalni broj.

Postoje brojevi kojima se u njihovu decimalnom zapisu znamenke nikada neće periodički ponavljati. Primjer takvog broja je $0.123456789101112131415.. .$

Zadatak 6.

Koristeći se računalom, odredi decimalni zapis sljedećih razlomaka.

a) $\frac{1}{9}$

b) $\frac{2}{7}$

c) $\frac{1}{6}$

d) $\frac{35}{99}$

a) $\frac{1}{9} = 0.11111.. . = 0 . \bar{1} = 0 . \dot{1}$

b) $\frac{2}{7} = 0.285714285714285.. . = 0 . \bar{285714} = 0 . \dot{2} 8571 \dot{4}$

c) $\frac{1}{6} = 0.16666666.. . = 0.1 \bar{6} = 0.1 \dot{6}$

d) $\frac{35}{99} = 0.3535353535.. . = 0 . \bar{35} = 0 . \dot{3} \dot{5}$

Zadatak 7.

Poveži odgovarajuće zapise.

$0.8383838.. .$	$0 . \bar{83}$
$0.8333333.. .$	$0.8 \bar{3}$
$0.8038038038.. .$	$0 . \bar{803}$
$0.803030303.. .$	$0.8 \bar{03}$

null

...i na kraju

Za kraj, uvježbaj pretvaranje iz jednog od zadanog zapisa broja (razlomak, decimalni broj ili postotak) u preostala dva zapisa.

Procijenite svoje znanje

Koju računsku operaciju (radnju) prikazuju razlomci?

zbrajanje

oduzimanje

množenje

dijeljenje

null

Broj iznad razlomačke crte naziva se

razlomka,

a broj ispod razlomačke crte

razlomka.

null

Dopuni.

Krug podijeljen na 10 dijelova. 7 dijelova obojano je ljubičastom bojom, dok 3 dijela nisu obojana.

Obojeno je sedam

kruga.

null

Spoji parove, mješoviti broj i njegov razlomački prikaz.

$3 \frac{4}{5} =$	$\frac{10}{5}$
$2 =$	$\frac{19}{5}$
$2 \frac{2}{5} =$	$\frac{12}{5}$
$3 \frac{1}{5} =$	$\frac{16}{5}$

null

Razvrstaj razlomke.

\frac{1}{4}

\frac{6}{7}

\frac{8}{7}

\frac{5}{3}

\frac{2}{3}

\frac{6}{2}

Pravi razlomak

Nepravi razlomak

null

Broj

4

zapisan u obliku razlomka s nazivnikom

8

ima brojnik jednak broju

null

Broj

2.34

čita se dva cijela trideset i četiri

null

Spoji odgovarajuće parove.

$\frac{43}{100}$	$0.43$
$\frac{43}{10}$	$0.043$
$\frac{43}{1 000}$	$4.3$
$\frac{43}{1}$	$43$

null

Nadopuni da vrijedi jednakost.

$\frac{37}{100} =$
$\frac{37}{1 000} =$
$\frac{37}{10} =$
$\frac{37}{10 000} =$

null

5.4 Zapis decimalnim brojem i razlomkom

Na početku...

Zanimljivost

Zanimljivost

Čitanje decimalnih brojeva

Istražimo

Kolekcija zadataka #1

Razlomački i decimalni zapis broja

Istražimo

Zadatak 1.

Zadatak 2.

Primjer 1.

Primjer 2.

Zadatak 3.

Postotci i promili

Zadatak 4.

Postotak

Primjer 3.

Istražimo

Primjer 4.

Zanimljivost

Promil

Primjer 5.

Zadatak 5.

Kolekcija zadataka #2

Beskonačni decimalni zapis

Primjer 6.

Zanimljivost

Zadatak 6.

Zadatak 7.

...i na kraju

Procijenite svoje znanje

Pravi razlomak

Nepravi razlomak

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

Razlomački zapis	$\frac{7}{10}$	$\frac{17}{10}$	$\frac{345}{10}$	$\frac{7}{100}$	$\frac{11}{100}$	$\frac{121}{100}$	$\frac{3}{1000}$	$\frac{27}{1000}$	$\frac{12345}{10000}$
Decimalni broj	$0.7$	$1.7$	$34.5$	$0.07$	$0.11$	$1.21$	$0.003$	$0.027$	$1.2345$