

Najviše zgrade na svijetu 2019. godine.
Crtež prikazuje deset trenutačno najviših građevina na svijetu. Koja od njih je najviša? Koja je druga, a koja treća po visini?
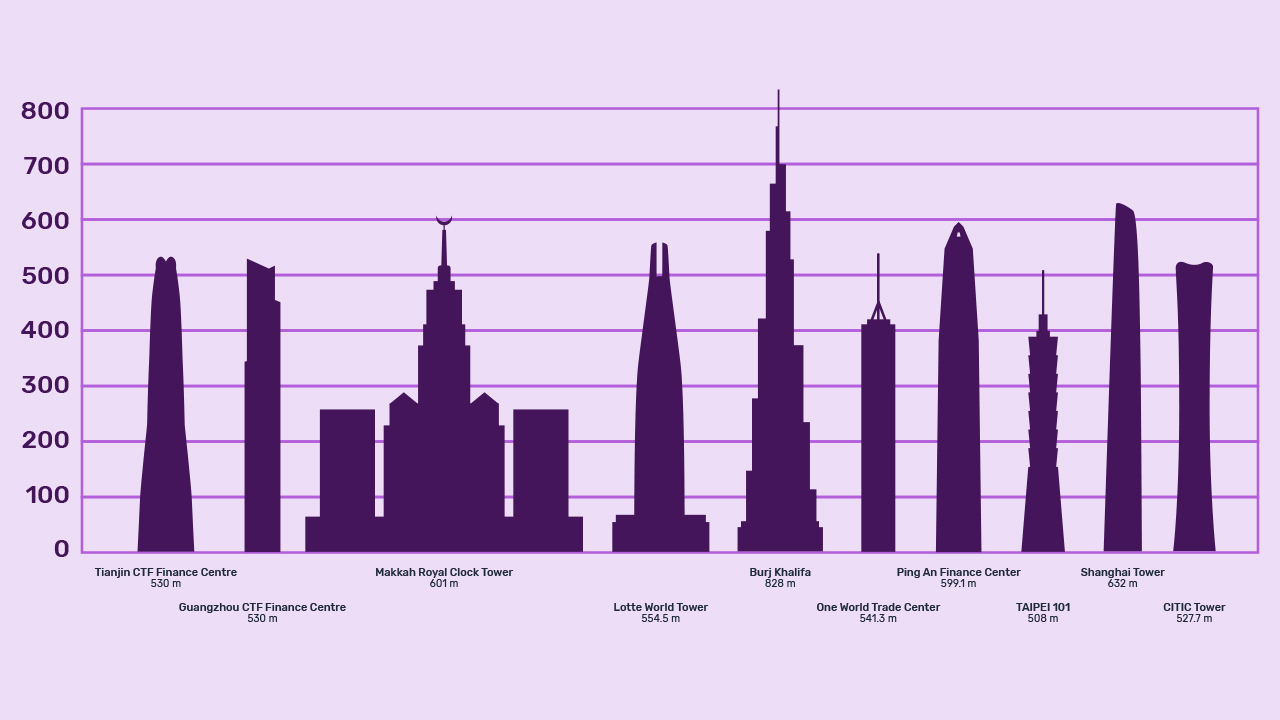
Da bismo odgovorili na ova pitanja, moguće je s crteža očitati (približnu) visinu pojedine zgrade ili se jednostavno osloniti na grafički prikaz.
U svakodnevnom životu često je potrebno odrediti koji je od dvaju brojeva veći.
Veličina prirodnog broja ovisi o broju znamenaka kojima je broj zapisan.
Činjenicu da je broj a manji od broja b zapisujemo
Istu činjenicu možemo napisati u obiku
Za svaki prirodni broj a vrijedi odnosno
Oznaku čitamo manje ili jednako, a oznaku čitamo veće ili jednako.
Primjer 1.
Ispišimo sve članove skupova i
Za bilo koja dva broja vrijedi točno jedna od sljedeće tri mogućnosti:
Ako za brojeve vrijedi i onda vrijedi
Nejednakosti i možemo kraće zapisati u obliku produljene nejednakosti
Primjer 2.
Ivan je visok a Petar Petar je viši od Ivana.
Pišemo: ili
Sanja je visoka Ona je viša od Ivana, a niža od Petra.
Pišemo: i ili kraće, u obliku produljene nejednakosti
U šest krugova napisani su sljedeći brojevi:
i
Poredaj krugove tako da dobiveni broj bude:
Primjer 3.
Učenici u razredu pripremaju proslavu i namjeravaju za svakog učenika kupiti po kolača i bočicu vode. Kolači su pakirani u kutije po komada, a voda u pakete po bočica. Koliko najmanje kutija kolača, a koliko paketa vode moraju kupiti ako su u tom razredu učenika?
U svakoj je kutiji broj kolača dovoljan za učenika. Budući da učenika ima zaključujemo da kutija neće biti dovoljno jer broj kolača mora biti najmanje Dakle, potrebno je kupiti najmanje kutija kolača.
U svakom je paketu broj bočica vode dovoljan za
učenika. Za
učenika nije dovoljno kupiti
paketa jer broj bočica mora biti najmanje
Dakle, potrebno je kupiti najmanje
paketa bočica vode.
| Ante | Branko | Damir | Filip | Goran | Ivo | Janko | Matko |
|---|---|---|---|---|---|---|---|
U tablici je prikazana statistika postignutih koševa na završnoj utakmici školskog košarkaškog prvenstva. Poredajte učenike prema broju postignutih koševa od učenika koji je postigao najviše koševa do učenika koji je postigao najmanje koševa.
Pomoću vage očitaj masu zadanog voća i povrća pa usporedi očitane mase.
Upiši broj manji od
i pokreni igru. Potrebno je složiti pločice sa zadanim brojevima po veličini, počevši od najmanje.