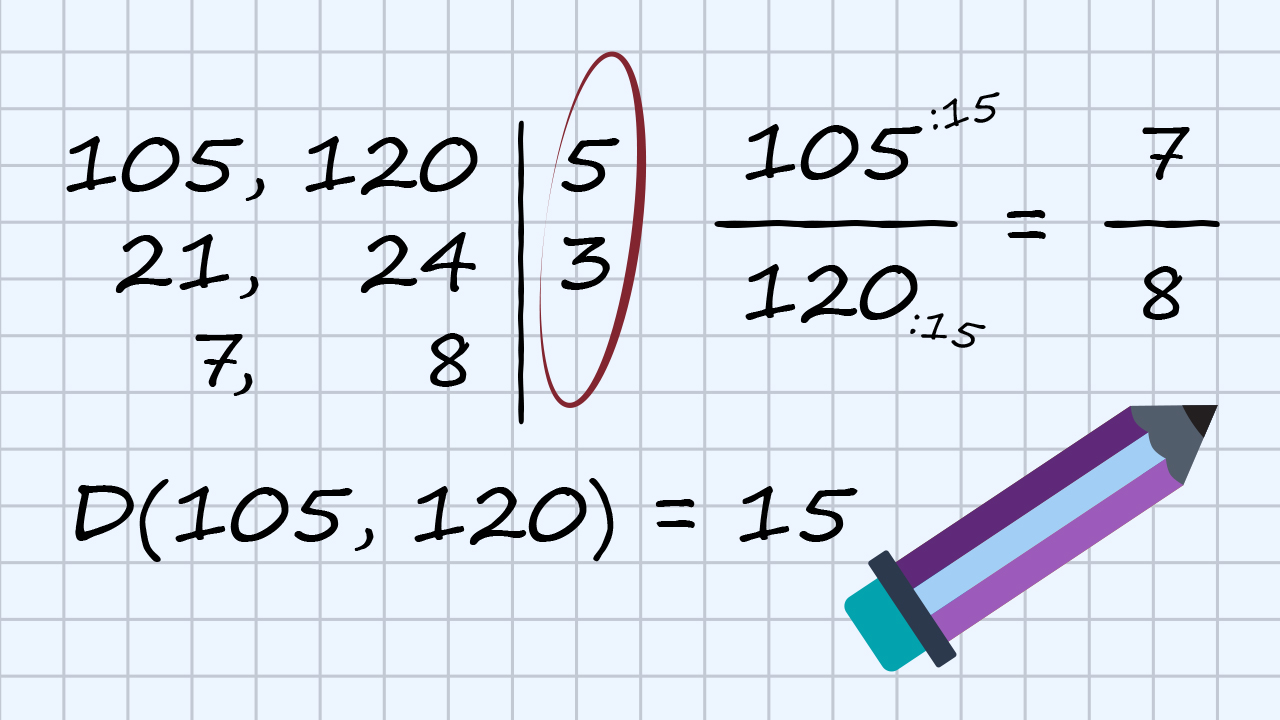


Primjer 1.
Na temelju crteža iz uvodnog zadatka zaključili smo da razlomci i imaju istu vrijednost pa možemo pisati
Možeš li računskim postupkom, bez crtanja, od dobiti
I brojnik i nazivnik možemo podijeliti brojem
Pišemo .
Taj se postupak naziva skraćivanje.
Skraćivanje razlomka
Skratiti razlomak znači i brojnik i nazivnik podijeliti istim brojem. Dobiveni i dani razlomak imaju istu vrijednost.
Primjer 2.
Skrati razlomke:
a. i
b.
a. Razlomak nije moguće skratiti jer i nemaju zajedničkih djelitelja osim broja Takav razlomak naziva se neskrativ razlomak.
b. Razlomak može se skratiti na više načina jer i imaju više zajedničkih djelitelja (osim broja ), a to su i
Dobiveni razlomak ne može se dalje skratiti jer brojnik i nazivnik nemaju zajedničkih djelitelja osim broja (s kojim nema smisla skraćivati). Za takav razlomak kažemo da je neskrativ ili da je skraćen dokraja.
Skrativ razlomak
Razlomak je skrativ ako se može skratiti, odnosno ako brojnik i nazivnik danog razlomka imaju barem jedan zajednički djelitelj osim broja
Neskrativ razlomak
Razlomak je neskrativ ako je brojnik i nazivnik nemaju zajedničkih djelitelja osim broja Za takav razlomak može se reći da je skraćen dokraja.
Brojnik i nazivnik neskrativog razlomka relativno su prosti brojevi.
Želimo li izbjeći postupno skraćivanje, posebice kod razlomaka koji imaju dvoznamenkaste (ili višeznamenkaste) nazivnike i brojnike, možemo prvo odrediti najveći mogući broj koji je djelitelj i brojnika i nazivnika pa izvršiti skraćivanje odjednom.
Taj je broj najveći zajednički djelitelj zadanih brojeva.
Najveći zajednički djelitelj
Najveći zajednički djelitelj brojeva i je najveći broj s kojim su djeljivi i broj i broj .
Najveći zajednički djelitelj brojeva i označavamo s
Primjer 3.
Skrati razlomak najvećim zajedničkim djeliteljem brojnika i nazivnika.
Uputa:
1. Odredi (pomoć, prema potrebi, potraži u rješenju primjera).
2. Skrati razlomak dobivenim brojem.
S obzirom na to da su brojnik i nazivnik veći dvoznamenkasti brojevi, nije svima jednostavno napamet odrediti da je najveći mogući broj s kojim su oba djeljivi broj
Postupak određivanja
možeš proučiti uz animaciju koja slijedi.
U animaciji je prikazan postupak nalaženja najvećega zajedničkog djelitelja primjenom tablice množenja, odnosno rastavljanjem brojeva na faktore (ne nužno proste), ali to nije i jedini mogući način.
Najveći zajednički djelitelj neka dva broja možeš odrediti na više načina. Najčešće se primjenjuju postupci:
1. napamet
2. rastavljanjem na faktore (primjena tablice množenja) te
3. primjena postupka s crtom.
Primjer 4.
Skrati odjednom razlomak
Najveći zajednički djelitelj brojnika i nazivnika je pa je trebalo i brojnik i nazivnik podijeliti tim brojem.
Je li ti bilo teško odrediti najveći zajednički djelitelj? Ako je, sljedeća animacija ti može pomoći.
Animacija koja slijedi prikazuje postupak s crtom koji ti može olakšati nalaženje najvećeg zajedničkog djelitelja brojnika i nazivnika zadanog razlomka.
Primijeni naučeno u sljedećim problemskim zadatcima.
Geografske karte mogu biti tiskane u različitim veličinama. Istraži mjerila koja se koriste na zidnim geografskim kartama, kartama koje su uvezane u atlas ili kartama koje su presavijene u knjižicu. Osmisli nekoliko zadataka koji su vezani uz tvoje istraživanje i podijeli ih s razrednim kolegama.
procijeni svoje znanje prije prelaska na sljedeću jedinicu!