

Linearna jednadžba s jednom nepoznanicom
je jednadžba oblika
gdje su
i
zadani brojevi.
Rješenje linearne jednadžbe je racionalni broj
koji uvršten u linearnu jednadžbu daje ispravnu jednakost.
Primjer 1.
Pronađi rješenje linearne jednadžbe
Za rješavanje ove jednadžbe treba oduzeti broj tri i s lijeve i s desne strane:
Jednadžbu zamislimo kao vagu koja ima lijevu i desnu stranu, a jednakost znači da su obje strane vage u ravnoteži. Ako s obje strane vage dodamo ili oduzmemo istu masu, vaga će ostati u ravnoteži.

Ako s obje strane jednadžbe dodamo ili oduzmemo isti broj, rješenje se neće promijeniti.
Poveži linearne jednadžbe s njihovim rješenjima.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Jednadžba je riješena ako na lijevoj strani ostane samo
U prethodnim linearnim jednadžbama dodavao se suprotan broj na obje strane jednadžbe. Otprije znamo kako je zbroj suprotnih brojeva jednak nula. Kada dodajemo suprotan broj na lijevu i desnu stranu jednadžbe, to možemo shvatiti kao da je broj koji je bio s lijeve strane jednadžbe prebačen na desnu stranu jednadžbe. Pri tom prebacivanju on je promijenio predznak.
Primjer 2.
Pronađi rješenje linearne jednadžbe
Za rješavanje ove jednadžbe treba broj četiri prebaciti na drugu stranu. Pritom mu treba promijeniti predznak:
Pomoć:
Poznatu veličinu na lijevoj strani prebaci na desnu stranu znaka jednakosti. Ne zaboravi pritom promijeniti predznak!
Primjer 3.
Koji broj je rješenje linearne jednadžbe
Rješenje ove jednadžbe dobit ćemo ako podijelimo i lijevu i desnu stranu s
Postupak rješavanja jednadžbe dijeljenjem može se pojednostavniti. To se može učiniti tako da se iza linearne jednadžbe napiše kosa crta i broj s kojim se dijeli. Uvijek se dijeli s onim brojem koji množi nepoznanicu:
Ako se obje strane jednadžbe podijele ili pomnože s istim brojem, rješenje ostaje isto.
Poveži linearne jednadžbe s odgovarajućim rješenjima.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Podijeli i lijevu i desnu stranu s brojem koji množi
Primjer 4.
Riješi linearnu jednadžbu i provjeri točnost dobivenog rješenja.
Pri rješavanju ove linearne jednadžbe treba prvo prebaciti broj na desnu stranu (i pritom mu promijeniti predznak), a potom cijelu jednadžbu podijeliti s
Za provjeru je li dobiveni broj rješenje jednadžbe, treba ga uvrstiti u jednadžbu i provjeriti daje li uvršteno rješenje točnu jednakost:
Pronađi rješenja linearnih jednadžbi.
Pomoć:
Prebaci poznate veličine s desne na lijevu stranu (ne zaboravi im promijeniti predznak). Ako se pored
nalazi broj, cijelu jednadžbu podijeli s tim brojem. Provjeri točnost rješenja.
Primjer 5.
Riješi linearnu jednadžbu i provjeri točnost rješenja.
Pri rješavanju ove linearne jednadžbe treba prebaciti na desnu stranu (i pritom mu promijeniti predznak), a potom cijelu jednadžbu podijeliti s
Provjera rješenja:
U prošlim zadatcima utvrđeno je kako poznate veličine, ako se nalaze na lijevoj strani jednadžbe, treba prebaciti na desnu stranu jednadžbe. Pritom im se mijenjao predznak.
Isto tako, ako se nepoznate veličine nalaze na desnoj strani jednadžbe, treba ih prebaciti na lijevu stranu jednadžbe. Ako mijenjaju stranu, treba i njima promijeniti predznak.
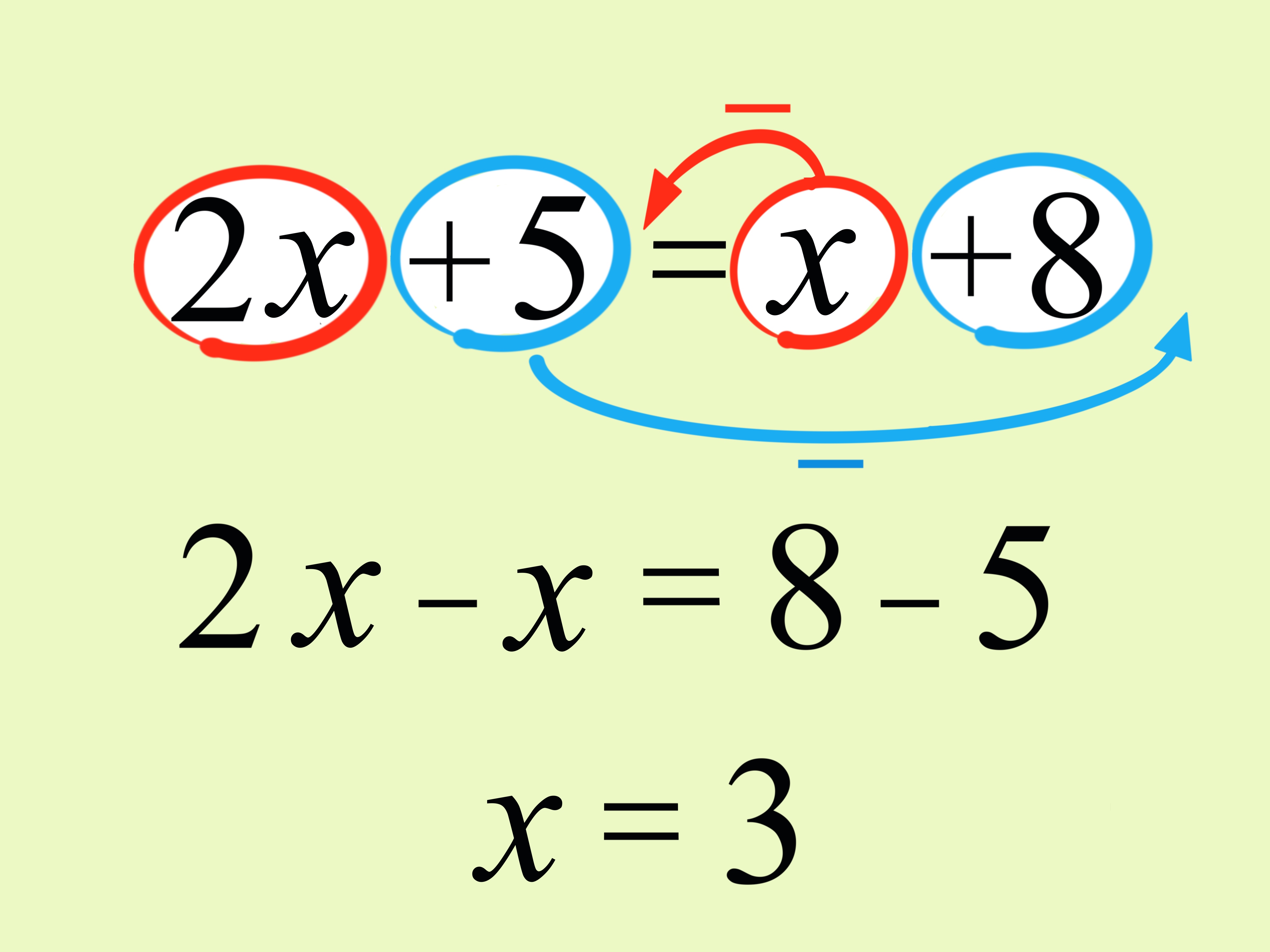
Primjer 6.
Riješi jednadžbu
Treba prvo nepoznate veličine prebaciti na lijevu, a poznate na desnu stranu. Potom treba zbrojiti sve poznate i sve nepoznate veličine.
Provjera:
Linearna jednadžba
riješena je u dva koraka. Svaki korak predstavlja jednostavniju jednadžbu, ali s istim rješenjem kao u zadanoj jednadžbi.
Jednadžbe s istim rješenjem nazivaju se ekvivalentne jednadžbe.
U linearnim jednadžbama s jednom nepoznanicom ponekad se nalaze i zagrade. U takvim ćeš se jednadžbama prvo riješiti zagrada koristeći se pravilima za rad sa zagradama.
Primjer 7.
Riješi jednadžbu
Treba se prvo riješiti zagrada, potom zbrojiti sve što se može na svakoj strani. Nepoznate veličine prebaciti na lijevu, a poznate na desnu stranu, a potom zbrojiti sve poznate i sve nepoznate veličine.
Provjera:
Pri rješavanju linearnih jednadžbi s razlomcima treba prvo pronaći najmanji zajednički nazivnik svih razlomaka u jednadžbi. Svaki član jednadžbe pomnoži se s tim brojem. Dobije se jednadžba ekvivalentna zadanoj jednadžbi, ali bez razlomaka.
Primjer 8.
Riješi jednadžbu
Pri rješavanju ove linearne jednadžbe prvo pronađi najmanji zajednički nazivnik svih razlomaka u jednadžbi, a potom i lijevu i desnu stranu jednadžbe pomnoži s tim brojem:
Provjera:
Riješi linearnu jednadžbu
Pomnoži lijevu i desnu stranu jednakosti s zajedničkim nazivnikom svih razlomaka u zadatku (s brojem ).
Za ponavljanje naučenog odigraj memory u kojem ćeš spojiti linearnu jednadžbu s njezinim rješenjem.