

U doba antičke Grčke najstarija grana matematike - geometrija, doživljava svoj procvat. Jedno od pitanja koje je zaokupljalo pažnju ondašnjih matematičara bilo je: može li se ravnalom i šestarom konstruirati kvadrat kojemu je površina dvostruko veća od površine zadanog kvadrata. U ovoj ćeš jedinici i ti naučiti kako s pomoću ravnala i šestara konstruirati paralelograme, pa pripremi potreban pribor. Ne zaboravi geometrijsku bilježnicu jer ćemo sve konstrukcije raditi u nju.
Starogrčki matematičari dugo su se bavili s tri problema: kvadratura kruga, duplikacija kocke i trisekcija kuta. Ako te zanima o čemu govore ti problemi, potraži informacije na internetu ili pitaj nastavnika Matematike.
Otprije ti je poznato da svaka konstrukcija mora imati analizu, konstrukciju i raspravu. Za svaki zadatak, u bilježnicu nacrtaj prvo skicu, a zatim konstruiraj zadani paralelogram.
Primjer 1.
Konstruiraj paralelogram kojemu su duljine susjednih stranica i a kut pri vrhu ima veličinu
Skica
Pri crtanju skice primjenjujemo pravila označavanja vrhova, duljina stranica i veličina kutova zadanog paralelograma.
Nacrtaj u bilježnicu skicu paralelograma te na njoj istakni zadane elemente, a zatim provjeri točnost rješenja uz pomoć sljedeće vježbe.
S obzirom na to da znaš konstruirati trokut prema konstrukcijama SSS, SKS i KSK, neće ti biti teško konstruirati paralelograme.
Ako bude potrebno, prisjeti se spomenutih konstrukcija trokuta i konstrukcija kutova zadanih veličina.
Zadanim elementima paralelogama pridruži položaj na slici opisan brojem.
Za svaki zadani element paralelograma na crtu upiši odgovarajući broj sa slike.

Pomoć:
Nasuprotne stranice jednakih su duljina.
Počevši od vrha
u smjeru suprotnom od smjera kretanja kazaljke sata, nalazi se stranica duljine
Konstruiraj zadani paralelogram, a zatim crtež usporedi s danim rješenjem.
1. Nacrtaj dužinu
duljine
kao na skici.
2. Konstruiraj kut veličine
s vrhom u točki
3. U šestar uzmi duljinu
zabodi ga u točku
i nacrtaj kružni luk koji siječe krak konstruiranog kuta. Dobiveno sjecište je, prema skici, točka
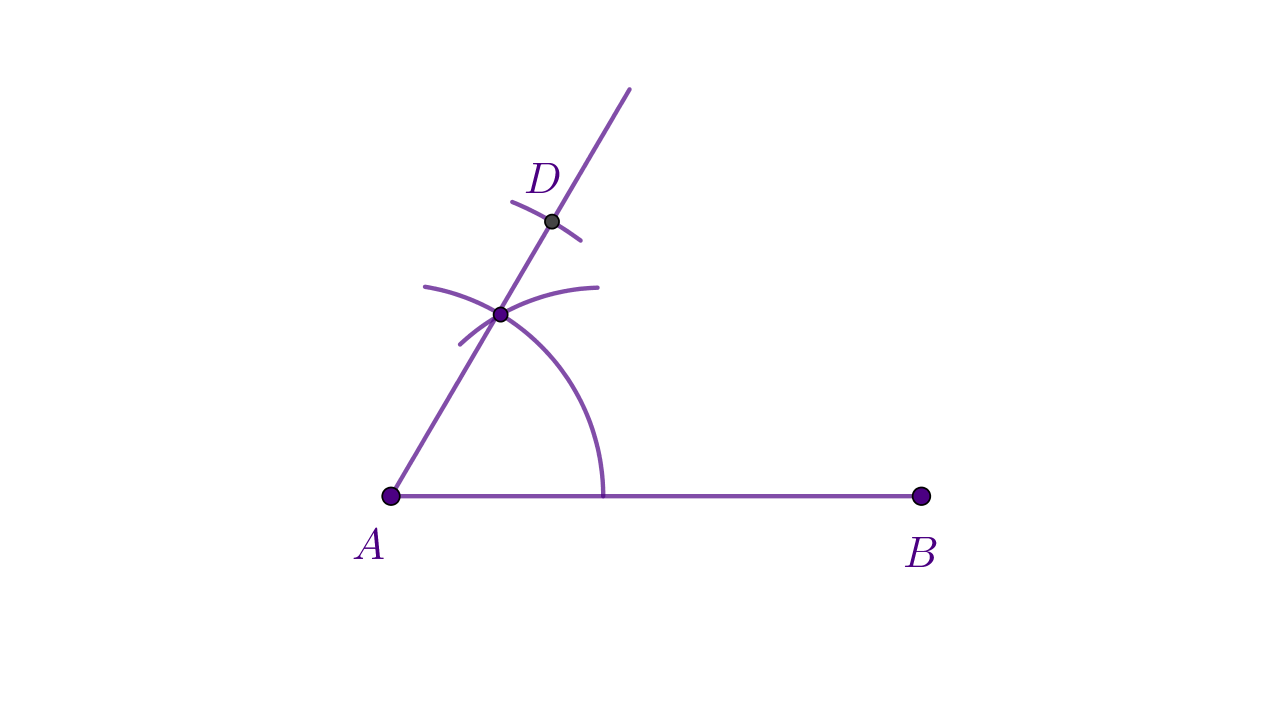
4. Iz točke
nacrtaj kružni luk polumjera
5. Iz točke nacrtaj kružni luk polumjera
6. Presjek kružnih lukova je točka
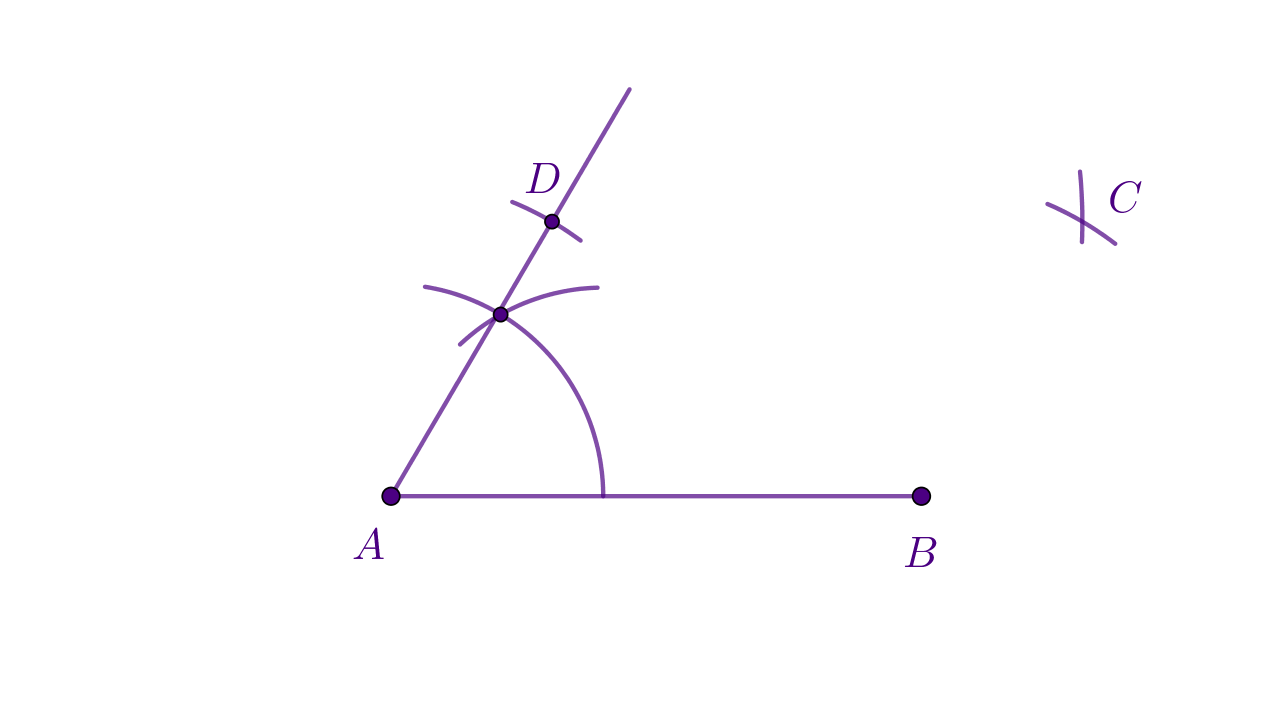
7. Spoji paralelogram
Rasprava:
Dijagonala
Prema otprije poznatim svojstvima paralelograma dovoljno je znati duljine dviju njegovih stranica i veličinu jednoga unutarnjeg kuta kako bi paralelogram bio jednoznačno određen. Postoji li još koji način?
Konstruiraj paralelogram
ako su zadani elementi:
i
Na skici označi zadane elemente.
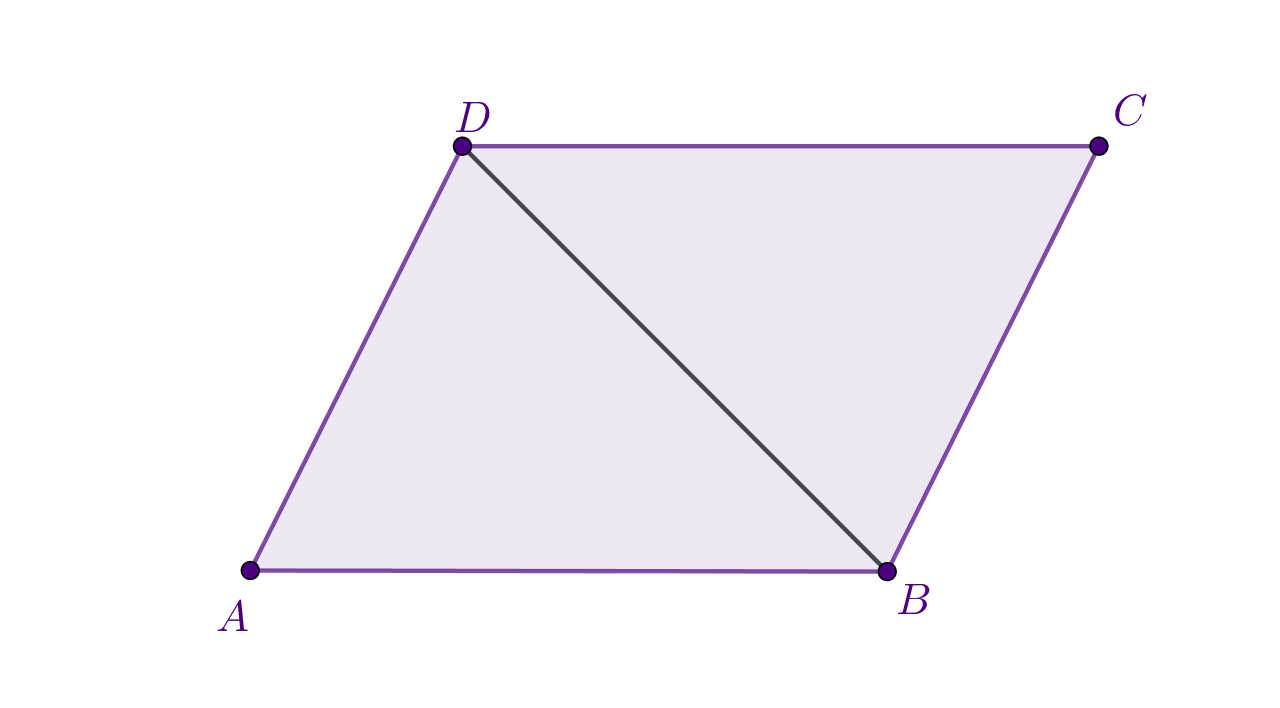
Pomoć:
Zadane elemente dovuci probližno na sredinu odgovarajuće stranice.
Postupak:
Počevši od vrha
prati smjer suprotan od smjera kretanja kazaljke sata.
Prema skici konstruiraj zadani paralelogram
Po potrebi, pomoć potraži u rješenju zadatka.
Prateći sljedeće korake, u bilježnicu konstruiraj zadani paralelogram.
Prema nacrtanoj skici prvo konstruiraj trokut prema konstrukciji SSS.

Sada iz vrha
nacrtaj kružni luk polumjera
a iz vrha
kružni luk polumjera
Presjek nacrtanih kružnih lukova četvrti je vrh paralelograma.
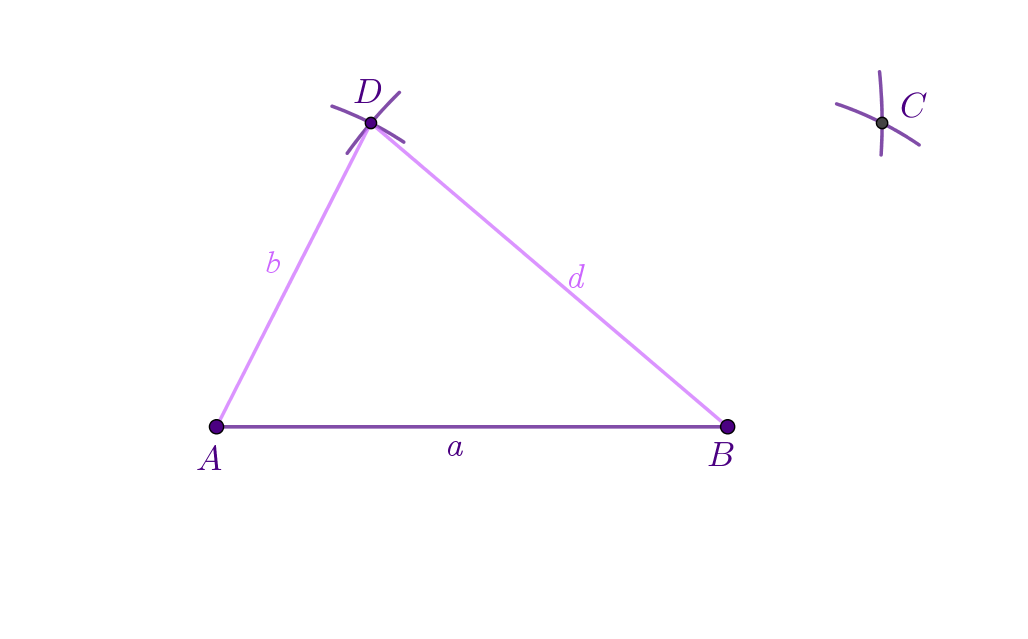
Spoji vrhove paralelograma.
Rasprava:
Konstruirani paralelogram u bilježnici sukladan je paralelogramu u rješenju zadatka.
Za konstrukciju zadanog paralelograma upotrebljavamo
Prema konstrukciji KSK konstruiraj trokut Ako je potrebno, prisjeti se konstrukcija kutova zadanih veličina. Zatim iz točke nacrtaj kružni luk polumjera Iz točke nacrtaj kružni luk polumjera Presjek kružnih lukova je četvrti vrh paralelograma
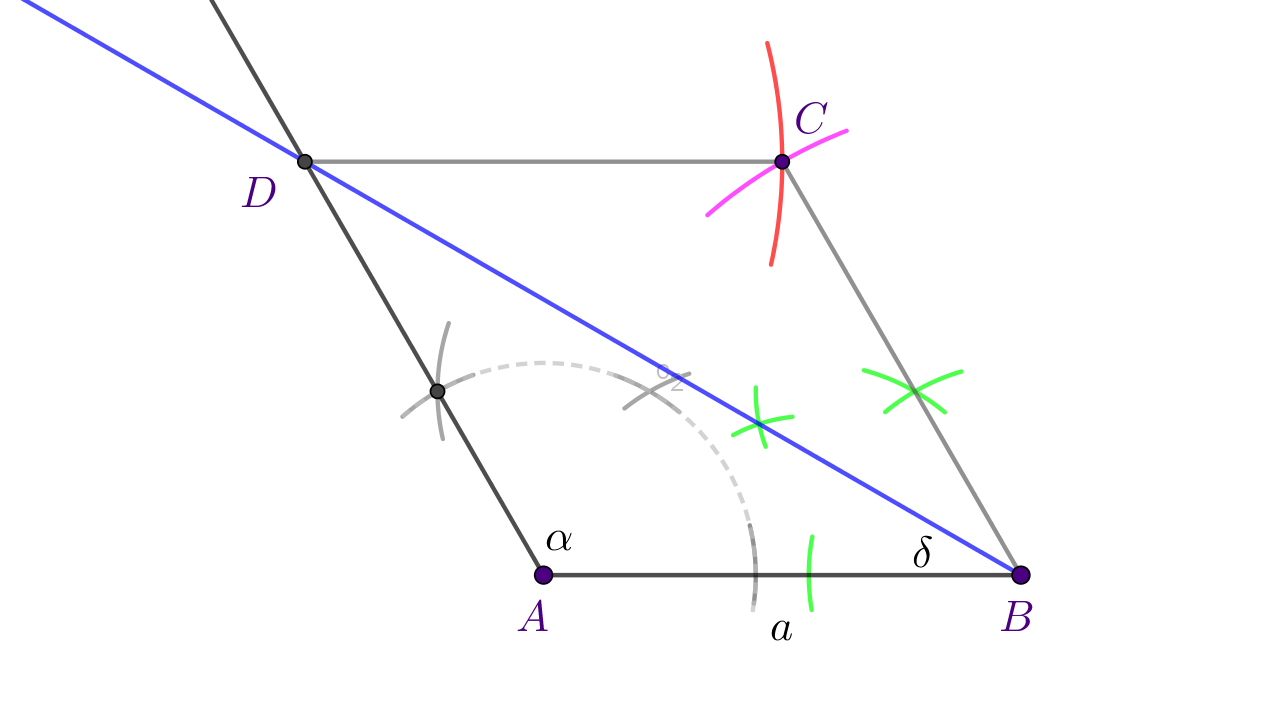
Rasprava:
Pomoć:
Da je zbroj veličina kutova koji pripadaju trokutu koji je zadan dvjema susjednim stranicama i dijagonalom paralelograma veći od
konstrukcija ne bi bila moguća.
Pomoć:
Ako su trokutu dva kuta jednakih veličina, tada je trokut jednakokračan. A s obzirom na to da su krakovi trokuta
ujedno i susjedne stranice paralelograma, zaključujemo da su te stranice sukladne.
Postupak:
Paralelogram kojemu su susjedne stranice jednakih duljina jest romb.
Pri konstrukciji pravokutnika primjenjujemo svojstva koja vrijede za taj geometrijski lik. Ponovimo ih.
Povlačenjem elemenata ponovi neka važna svojstva pravokutnika.
|
Susjedne su stranice
|
međusobno okomite. |
|
Dijagonale se
|
pravi. |
|
Dijagonale su
|
jednakih duljina i usporedne. |
|
Nasuprotne su stranice
|
međusobno raspolavljaju. |
|
Svi su kutovi
|
jednakih duljina. |
Primjer 2.
Konstruiraj pravokutnik kojemu susjedne stranice imaju duljine i a zatim pravokutniku konstruiraj opisanu kružnicu.
Skica:
Dovuci zadani element u pravilno nacrtanu skicu pravokutnika zadanog u zadatku.
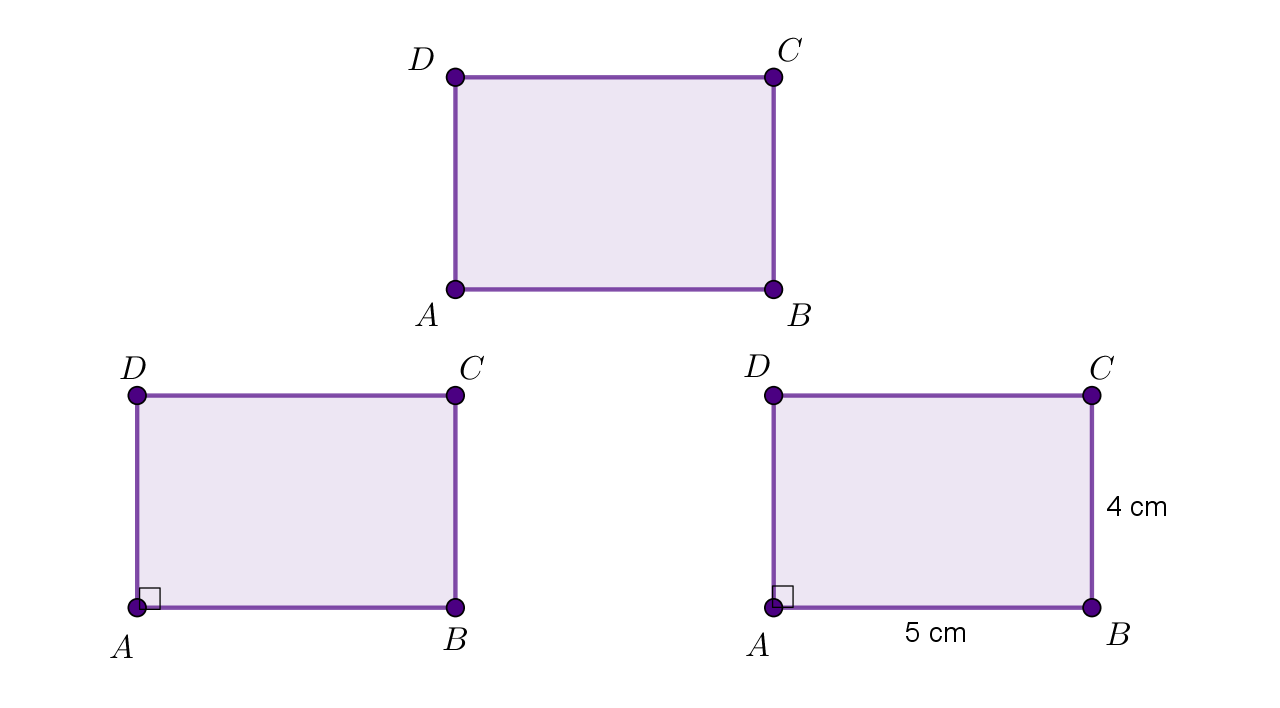
Pomoć:
Skica mora sadržavati naznačeni pravi kut i duljine stranica kako bismo pri konstrukciji pravilno upotrebljavali zadane elemente konstrukcije.
Usporedi konstruirani pravokutnik s rješenjem.
S obzirom na to da se radi o konstrukciji, i pravi je kut potrebno konstruirati ravnalom i šestarom.
U bilježnici nacrtaj dužinu
duljine
Konstruiraj pravi kut s vrhom u točki
Iz istog vrha nacrtaj kružni luk polumjera
koji presijeca nacrtani polupravac, odnosno krak pravoga kuta. Dobiveno je sjecište vrh
pravokutnika.
Sada iz vrha nacrtaj kružni luk polumjera Iz vrha nacrtaj kružni luk polumjera Sjecište kružnih lukova je točka četvrti vrh pravokutnika.

Spoji vrhove pravokutnika.
Odaberi točku koja je središte pravokutniku opisane kružnice.
Pomoć:
Pravokutniku opisana kružnica prolazi svim vrhovima pravokutnika.
Konstruiranom pravokutniku opiši kružnicu, a potom provjeri rješenje.
Konstruiraj pravokutnik kojemu je duljina dijagonale a kut između dijagonala
Ne zaboravi nacrtati skicu prije same konstrukcije.
Prouči skicu i prati opis konstrukcije.
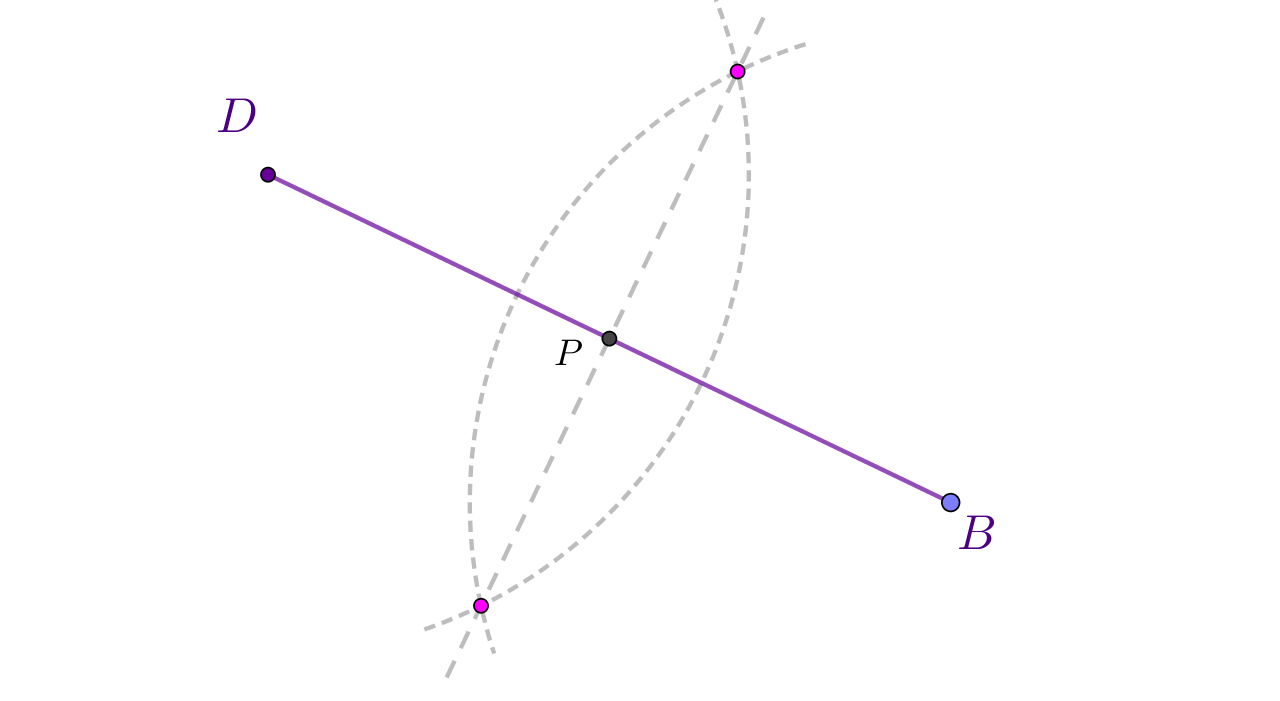
Nacrtaj dužinu duljine Ako ti je lakše, nacrtaj dužinu malo ukoso, kao što je na skici.
Vrh kuta koji zatvaraju dijagonale je sjecište dijagonala, odnosno polovište bilo koje dijagonale. Zato konstruiraj polovište nacrtane dužine.
Sada konstruiraj kut veličine
s vrhom u točki
, a krak produži i preko točke
da dobiješ pravac kojem pripada druga dijagonala.
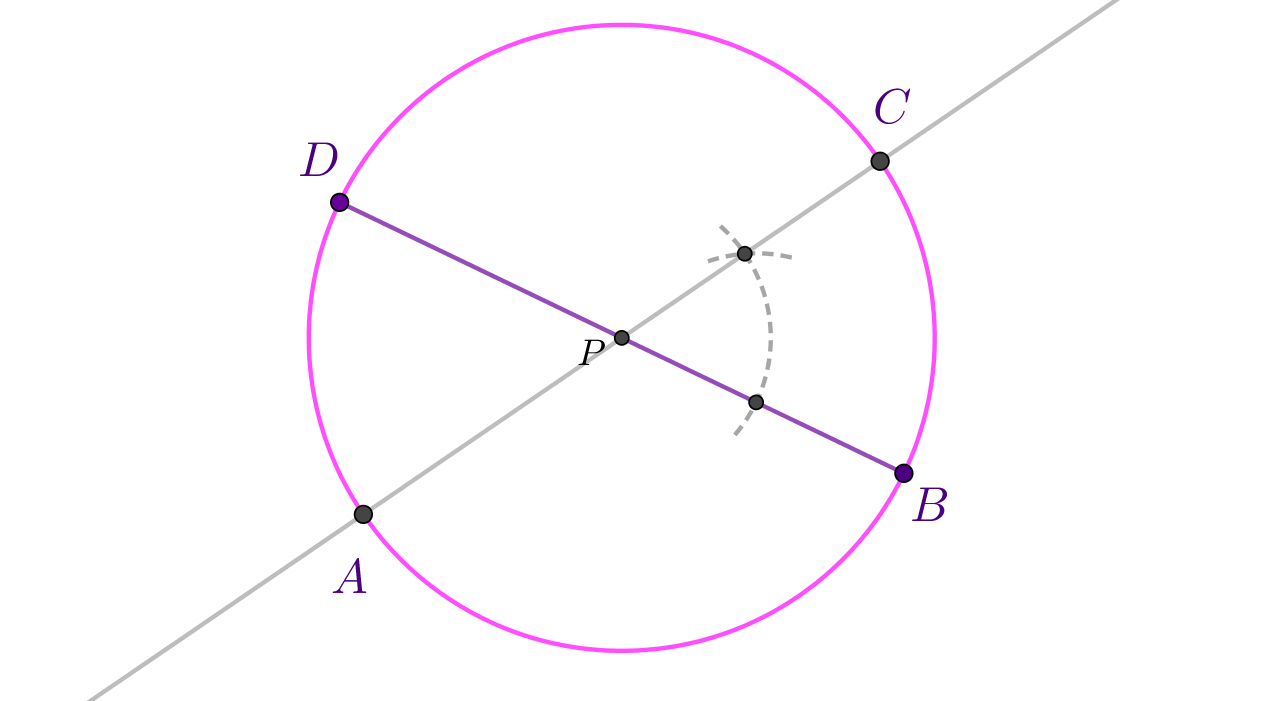
Zabodi šestar u točku
rastegni ga do točke
ili točke
pa nacrtaj kružnicu, odnosno nacrtaj kružnicu sa središtem u
polumjera
.
Sjecišta kružnice i pravca, točke i vrhovi su pravokutnika.
Spoji vrhove pravokutnika.
Dobro poznavanje svojstava kvadrata pomoći će pri konstrukciji kvadrata.
Primjer 3.
Konstruiraj kvadrat kojemu je stranica duljine
Nacrtaj skicu i razmisli o koracima konstrukcije.
Prvo nacrtaj skicu na kojoj ćeš označiti vrhove kvadrata i istaknuti zadane elemente.
Konstukciju započni crtanjem dužine zadane duljine. Konstruiraj pravi kut s vrhom u točki (ili u svejedno je). Kako su stranice kvadrata jednakih duljina, na nacrtanom kraku pravog kuta šestarom odmjeri dužinu duljine te označi točku Kao pri konstrukciji svakog paralelograma sada iz i nacrtaj kružne lukove polumjera Njihovo sjecište označi s
Spoji vrhove kvadrata.
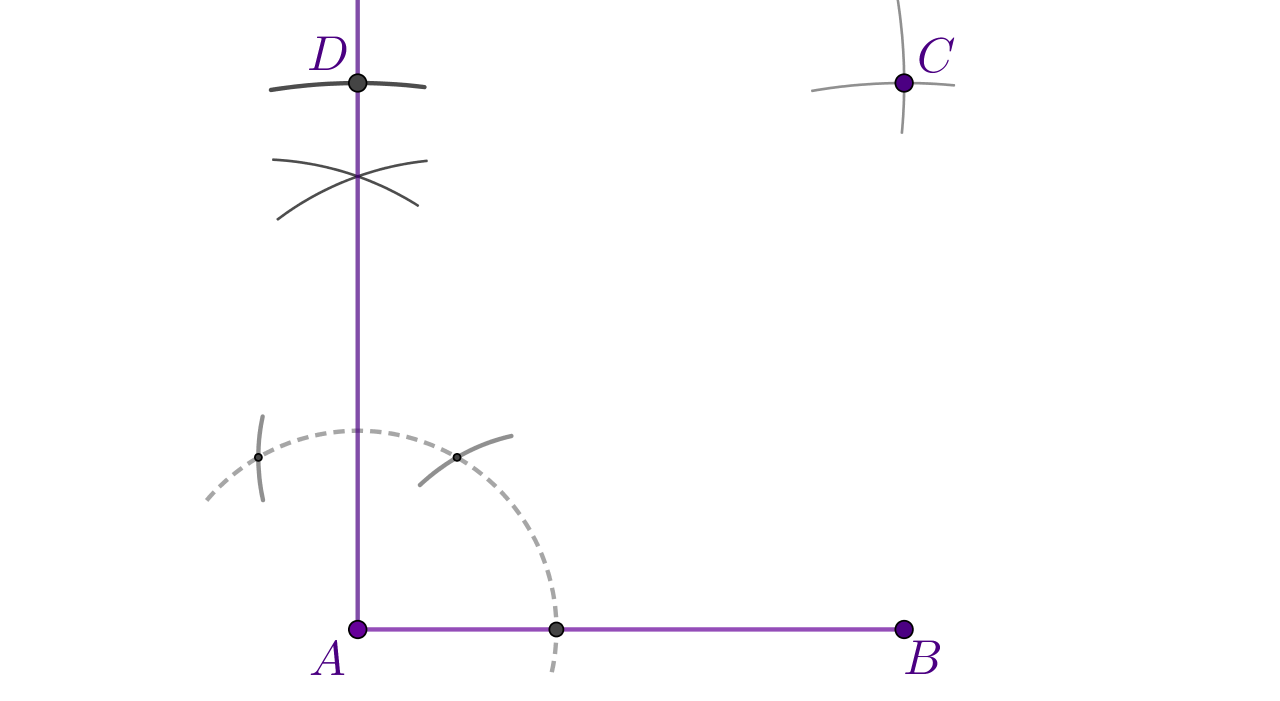
Konstruiranom kvadratu želimo opisati i upisati kružnicu.
Razmisli o koracima konstrukcije, dopuni prethodnu skicu i svoja razmišljanja usporedi sa sljedećim zadatcima.
Izvrši konstrukciju.
Sjecište dijagonala kvadrata je središte kvadratu i opisane i upisane kružnice.
Primjer 4.
Konstruiraj kvadrat čija je dijagonala duljine
Prije konstrukcije nacrtaj skicu i razmisli o koracima konstrukcije. Svoja razmišljanja možeš provjeriti u dvama pitanjima koja slijede.
Koje ćeš od navedenih svojstava kvadrata prvo iskoristiti trebaš li konstruirati kvadrat kojemu je zadana duljina dijagonale
Pomoć:
Sve su tvrdnje točne, ali samo jednu od njih možeš iskoristiti za prvi korak konstrukcije. Još jednom pročitaj zadatak. Koji je podatak poznat o kvadratu?
Nacrtaj skicu. Razmisli o koracima konstrukcije i dopuni rečenice.
Prvo crtam
Pomoć:
Konstrukcija može započeti i crtanjem druge dijagonale.
Konstrukcija prikazana na slici izvodi se prema koracima iz prethodnog zadatka. Potrebno je još spojiti točke
i
Usporedi sa svojim rješenjem.
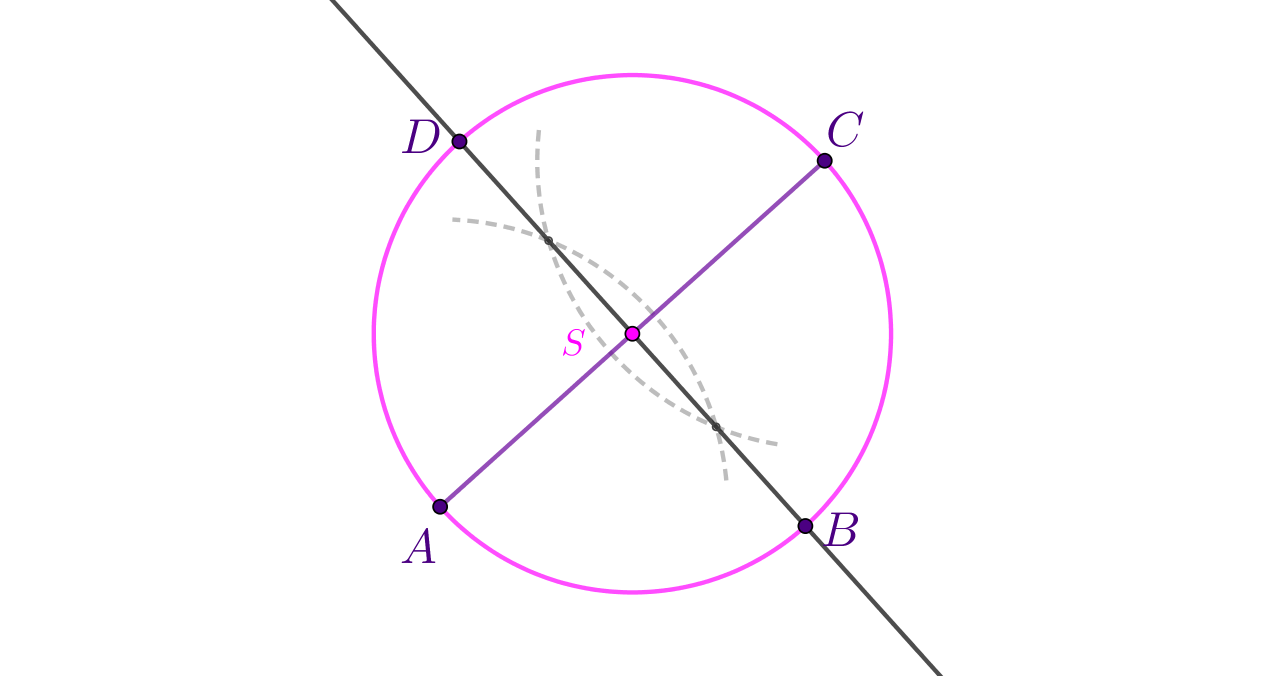
Istraži na koji su način stari Grci riješili problem konstrukcije kvadrata iz uvodnog zadatka.
Konstruiraj, prema rezultatima svoga istraživanja, kvadrat koji ima površinu dvostruko veću od površine zadanog kvadrata.
Za sada još nemaš dovoljno znanja dokazati točnost postupka, ali čim naučiš Pitagorin poučak, moći ćeš i to.
Romb je paralelogram kojemu su stranice jednakih duljina, a paralelograme već znamo konstruirati.
Konstruiraj romb čije stranice zatvaraju kut veličine i imaju duljinu Rombu upiši kružnicu.
Nacrtaj skicu i razmisli o koracima konstrukcije.
Konstruiraj kut s vrhom u Ako je potrebno, prisjeti se konstrukcije kuta. Na krakovima kuta nacrtaj kružne lukove radijusa . Označi, prema skici, vrhove i Iz obje te točke nacrtaj kružne lukove istih radijusa. Njihovo sjecište označi s
Spoji vrhove romba.
Sada iz sjecišta dijagonala nacrtaj okomicu do jedne stranice. Duljinu te dužine uzmi u šestar i iz sjecišta dijagonala nacrtaj kružnicu.
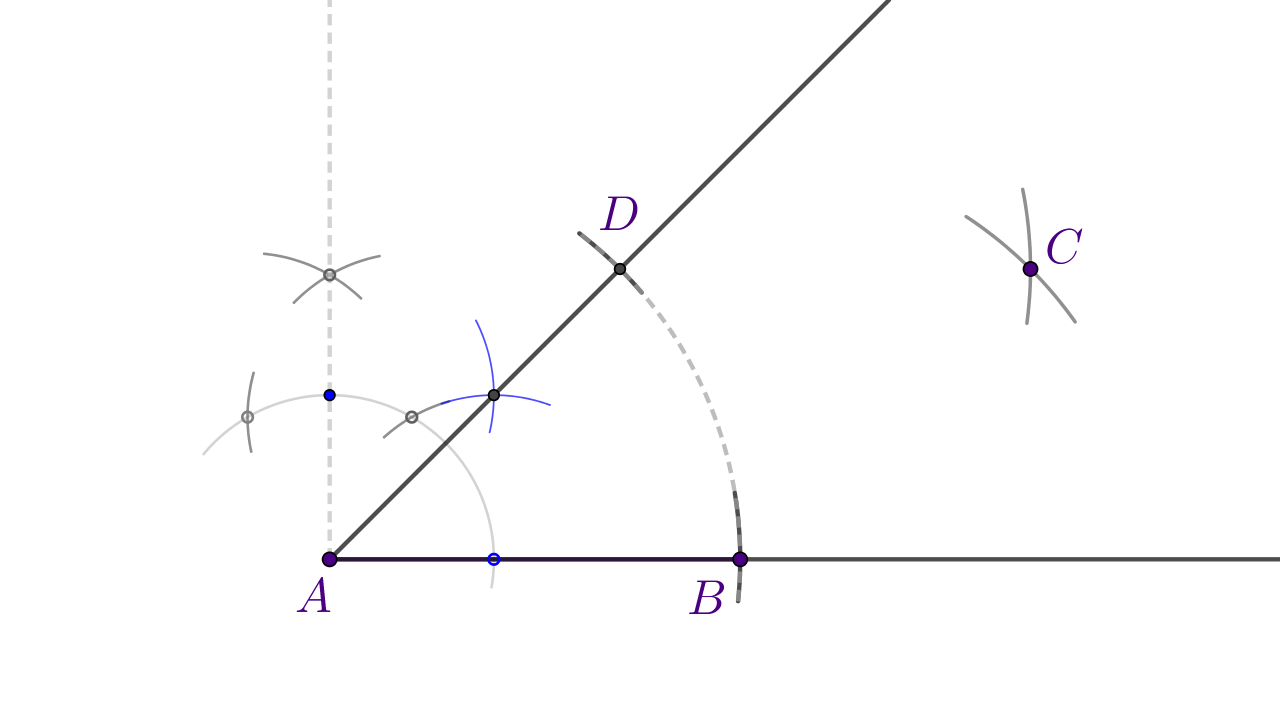
Izradi vježbu
Pitaj nastavnika Matematike ili na internetu potraži model tangram slagalice ili ga izradi prema uputama. Od dijelova tangrama složi pravokutnik, paralelogram i kvadrat.
Za slaganje svakog lika moraš upotrijebiti svih sedam dijelova, oni se ne smiju međusobno preklapati, ali ih možeš okrenuti na drugu stranu. Sretno!

Francuski matematičar, Pierre Varignon (1654. – 1722.), otkrio je jednu zanimljivu činjenicu vezanu uz četverokute i paralelograme. Poigraj se s nacrtanim četverokutom mijenjajući duljine njegovih stranica tako što ćeš povlačiti vrhove. Pokušaj odgonetnuti što je to zapazio ovaj poznati matematičar.