Matematika 6 - 6.3 Pravokutni koordinatni sustav u ravnini

Na početku...

GPS lokatori služe za pronalaženje izgubljenih osoba, životinja ili ukradenih stvari. Iza svih GPS uređaja stoje geografske koordinate, odnosno geografska širina i geografska dužina neke lokacije. Geografska širina i dužina su uređeni parovi brojeva koji odgovaraju točno jednoj točki u geografskoj mreži. U matematici uređeni par brojeva pripada točno jednoj točki u mreži koja se zove koordinatni sustav u ravnini.

GPS lokator

Pravokutni koordinatni sustav u ravnini

Zanimljivost

Legenda kaže da je ideju za uvođenjem pravokutnog koordinatnog sustava dobio u 17. stoljeću francuski matematičar Rene Descartes kada je bio bolestan i iz kreveta gledao muhu kako hoda po kvadratnim pločicama. Rene Descartes je jedan od najvažnijih matematičara svog vremena. Uvođenjem pravokutnog koordinatnog sustava prvi je povezao geometriju i aritmetiku u novu granu matematike, analitičku geometriju.

Pravokutni koordinatni sustav u ravnini dobijemo ako nacrtamo dva okomita brojevna pravca koji se sijeku u ishodištu svakog od njih. U animaciji pogledaj kako se definira i crta pravokutni koordinatni sustav u ravnini.

Zadatak 1.

Slijedeći korake iz animacije nacrtaj u bilježnicu pravokutni koordinatni sustav u ravnini.

Pravokutni koordinatni sustav s osima x i y. — Pravokutni koordinatni sustav u ravnini

Zanimljivost

Razni su nazivi za koordinatne osi, primjerice u projektu STRUNA (Hrvatsko strukovno nazivlje) Instituta za jezik i jezikoslovlje nalazimo os apscisa i os ordinata. Matematički rječnik profesora Ivice Gusića spominje i koordinatne osi os apscisa i os ordinata, te x-os i y-os, dok u Hrvatskoj enciklopediji Leksikografskog zavoda Miroslav Krleža stoji: "Koordinate se tada zovu apscisa (na osi x) i ordinata (na osi y)". U Rječniku znanstvenog nazivlja Bogoslava Šuleka, prvog rječnika te vrste u Hrvata, koji je tiskan 1874.-1875. godine, pod koordinate se spominju nuzrednice i surednice.

Razmisli i odgovori.

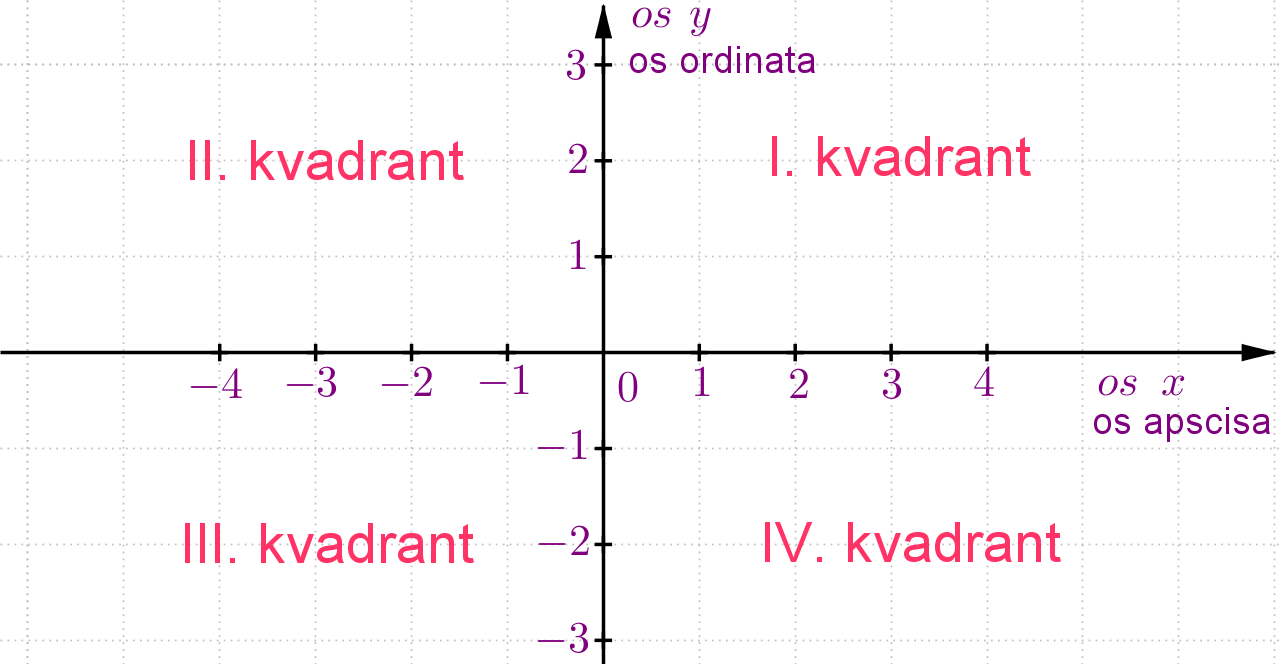
Koordinatnim osima $x$ i $y$ ravnina je podijeljena na

jednaka

dijela.

Pomoć:

Nacrtaj još jednom pravokutni koordinatni sustav u ravnini i razmisli na koliko dijelova dva okomita pravca mogu podijeliti ravninu.

Dijelove ravnine koje dobijemo kada nacrtamo koordinatne osi nazivamo kvadranti.

Četiri kvadranta pravokutnog koordinatnog sustava

Četiri kvadranta u pravokutnom koordinatnom sustavu. Prvi kvadrant gore desno, drugi kvadrant gore lijevo, treći kvadrant dolje lijevo, četvrti kvadrant dolje desno.

Uređeni parovi i koordinate točaka u pravokutnom koordinatnom sustavu u ravnini

Da bismo točku smjestili na brojevni pravac treba nam jedna koordinata. Pridruživanje racionalnog broja $x$ točki $T$ na brojevnom pravcu zapisujemo $T (x) .$ Ako točku želimo smjestiti u ravninu u kojoj su dva brojevna pravca, trebamo dvije koordinate.

Par brojeva u kojem se

zna koji broj je na

, a koji na drugom mjestu je

prvom mjestu

uređeni par

točno

Pomoć:

Dopuni rečenicu tako da ima smisla.

null

Uređenim parovima pridružujemo točke pravokutnog koordinatnog sustava u ravnini. Pri tome prvi član uređenog para potražimo na vodoravnoj osi $x,$ a drugi član na vertikalnoj osi $y .$ Točka se u pravokutnom koordinatnom sustavu u ravnini nalazi na sjecištu pravaca usporednih s koordinatnim osima.

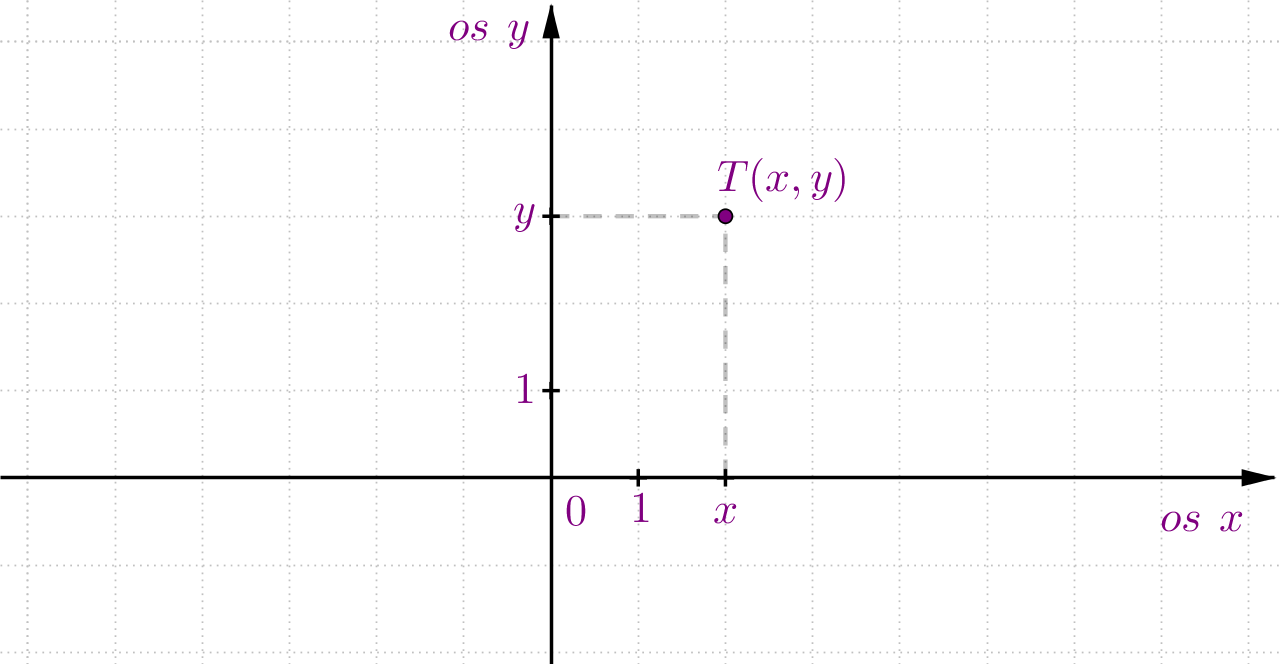
Uređenom paru (x, y) pridružena točka u pravokutnom koordinatnom sustavu u ravnini. — Točka u pravokutnom koordinatnom sustavu u ravnini

Kada nekom uređenom paru pridružimo točku $T$ u pravokutnom koordinatnom sustavu u ravnini to zapisujemo kao $T (x, y) .$

Primjer 1.

Uređenom paru $(3, 2)$ pridruži točku $T$ u pravokutnom koordinatnom sustavu. Pokušaj u bilježnicu samostalno riješiti zadatak, zatim usporedi svoje rješenje s ponuđenim.

Nacrtamo pravokutni koordinatni sustav u ravnini. Označimo koordinatne osi $x$ i $y,$ ishodište i jedinične točke. Prvi član uređenog para je broj $3,$ a drugi član je broj $2 .$ Na osi $x$ pronađemo prvi član zadanog uređenog para (točku s koordinatom $3$ ) i od te točke povučemo (crtkano) dio pravca usporedno s osi $y .$ Na osi $y$ pronađemo drugi član istog uređenog para (točku s koordinatom $2$ ) i od nje povučemo dio pravca usporednog s osi $x .$ U njihovom sjecištu se nalazi točka $T (3, 2) .$

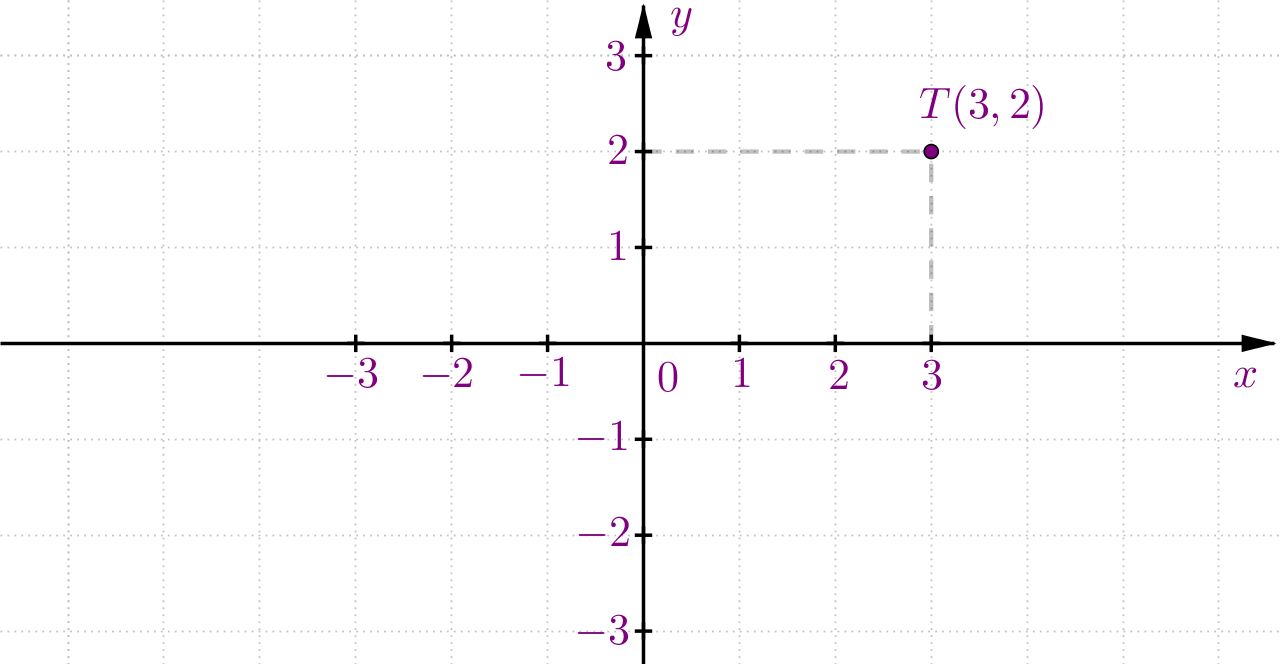
Uređenom paru (3, 2) pridružena točka T u pravokutnom koordinatnom sustavu u ravnini. — Točka u pravokutnom koordinatnom sustavu u ravnini

Koordinate točke u pravokutnom koordinatnom sustavu

Članove uređenog para kome je pridružena točka $T (x, y)$ nazivamo koordinate točke $T .$ Prvu koordinatu nazivamo apscisa, a drugu ordinata točke $T .$

Zadatak 2.

Zadana je točka $T (- 3, 5) .$

Apscisa točke $T$ je
Ordinata točke $T$ je

Pomoć:

Dobro pogledaj koordinate točke $T$ i razmisli.

Postupak:

Prvi član uređenog para je apscisa točke, a drugi član je ordinata točke u pravokutnom koordinatnom sustavu u ravnini.

Točke u pravokutnom koordinatnom sustavu u ravnini

Ucrtati neku točku $T (x, y)$ u pravokutni koordinatni sustav u ravnini znači zadanom uređenom paru pridružiti točku $T .$

Zadatak 3.

Ucrtaj u pravokutni koordinatni sustav točke $A (3, - 1),$ $B (- 3, - 2),$ $C (- 2, 3)$ i $D (1, 4) .$

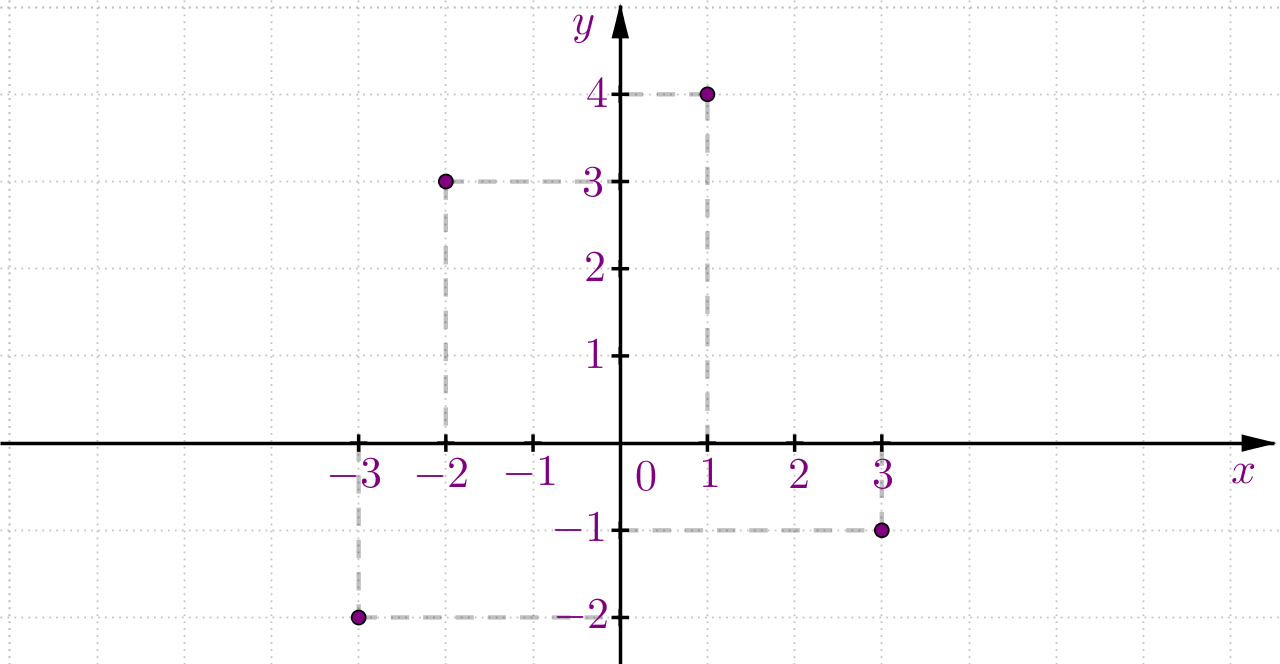
U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke koje treba pridružiti uređenim parovima.

D (1, 4)

C (- 2, 3)

B (- 3, - 2)

A (3, - 1)

Pomoć:

U ponuđenom pravokutnom koordinatnom sustavu u ravnini već su ucrtane točke pridružene uređenim parovima, treba razmisliti kojem uređenom paru je pridružena koja točka.

Postupak:

Prvu koordinatu uređenog para pronalazimo na osi $x,$ a drugu na osi $y .$

Zadatak 4.

Ucrtaj u pravokutni koordinatni sustav točke $A (- 2, - 2),$ $B (3, 1),$ $C (- 1, 4)$ i $D (1, - 1) .$ Pokušaj u bilježnicu samostalno riješiti zadatak, zatim usporedi svoje rješenje s ponuđenim.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke koje su pridružene uređenim parovima. — Točke u pravokutnom koordinatnom sustavu u ravnini

Zadatak 5.

Ucrtaj u pravokutni koordinatni sustav točke $A (3, - 2),$ $B (- 3, 2)$ i $C (- 3, - 2) .$ Spoji točke tako da dobiješ trokut $A B C .$ Pokušaj u bilježnicu samostalno riješiti zadatak, zatim usporedi svoje rješenje s ponuđenim.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke pridružene uređenim parovima iz zadatka. — Trokut u pravokutnom koordinatnom sustavu u ravnini

Nacrtani trokut $A B C$ je

trokut.

Površina tog trokuta je

kvadratnih

jedinica.

Pomoć:

Prebroji koliko jediničnih duljina ima od točke $C$ do točke $B,$ to je duljina katete $a .$ Zatim prebroji koliko jediničnih duljina ima od točke $C$ do točke $A,$ to je duljina katete $b .$ Površinu izračunaj po formuli za površinu pravokutnog trokuta.

Postupak:

$P = \frac{4 \cdot 6}{2}$

Zadatak 6.

Ucrtaj u pravokutni koordinatni sustav točke $A (1, 4),$ $B (- 1, - 3)$ i $C (3, - 3) .$ Spoji točke tako da dobiješ trokut $A B C .$ Pokušaj u bilježnicu samostalno riješiti zadatak, zatim usporedi svoje rješenje s ponuđenim.

Nacrtani trokut je

trokut.

Površina tog trokuta je

kvadratnih

jedinica.

Pomoć:

Prebroji koliko jediničnih duljina ima od točke $B$ do točke $C,$ to je duljina osnovice $a .$ Zatim prebroji koliko jediničnih duljina ima od polovišta dužine $\bar{B C}$ do točke $A,$ to je duljina visine $v_{a} .$ Površinu izračunaj po formuli za površinu trokuta.

Postupak:

$P = \frac{a \cdot v_{a}}{2} = \frac{4 \cdot 7}{2}$

Zadatak 7.

Ucrtaj u pravokutni koordinatni sustav točke $A (3, - 3),$ $B (3, 1),$ $C (- 1, 1),$ $D (- 1, - 3)$ i $E (1, 4) .$ Spoji točke redom $A,$ $B,$ $C,$ $D,$ $B,$ $E,$ $C,$ $A,$ $D .$ Pokušaj u bilježnicu samostalno riješiti zadatak, zatim usporedi svoje rješenje s ponuđenim.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su i spojene točke A, B, C, D i E pridružene uređenim parovima. — Točke u pravokutnom koordinatnom sustavu u ravnini

Zadatak 8.

Odredi koordinate točaka $A,$ $B,$ $C$ i $D$ sa slike. Spoji parove.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke A, B, C i D.

$B$	$(3, 1)$
$A$	$(- 1, 3)$
$C$	$(1, - 3)$
$D$	$(- 3, - 4)$

Pomoć:

Dobro pogledaj položaj točaka u pravokutnom koordinatnom sustavu u ravnini i razmisli.

Postupak:

Apscisu točke čitamo sa osi $x,$ a ordinatu čitamo sa osi $y .$

Točke na koordinatnim osima

Zadatak 9.

Ucrtaj točke

A (0, 3),

B (4, 0),

C (0, - 3)

D (- 2, 0)

u pravokutni koordinatni sustav u ravnini.

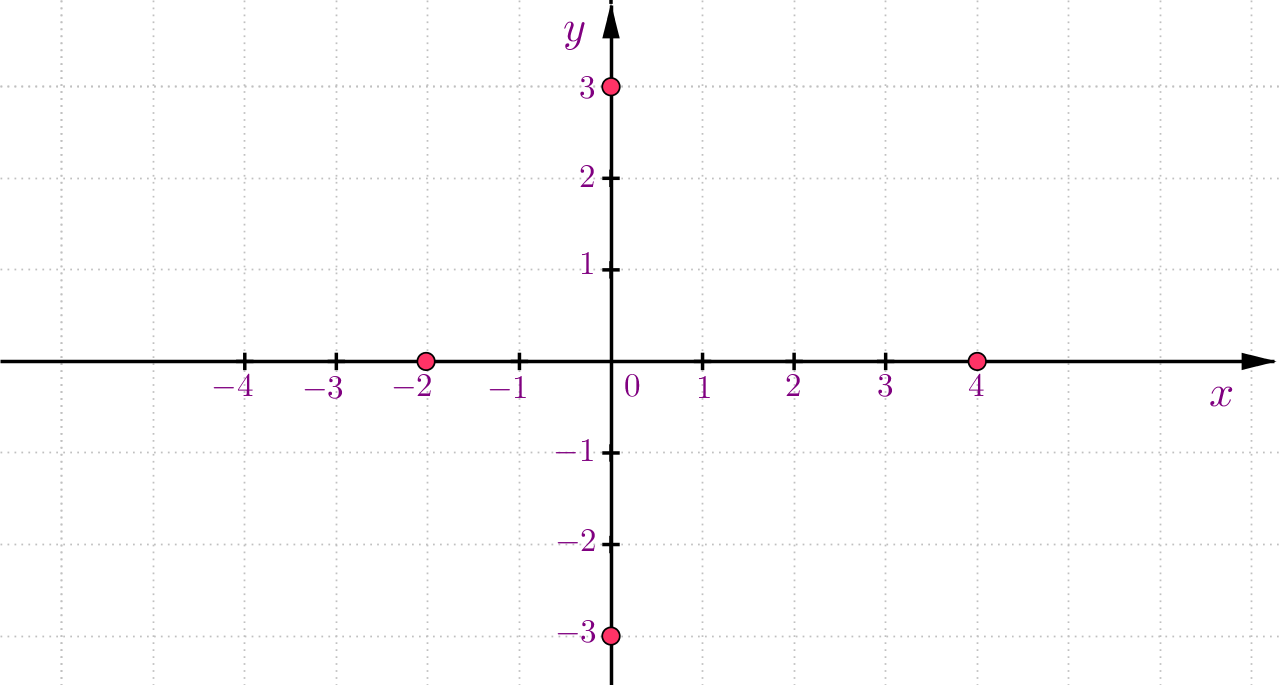
Na koordinatnim osima ucrtane su točke koje treba pridružiti uređenim parovima.

A (0, 3)

B (4, 0)

C (0, - 3)

D (- 2, 0)

Pomoć:

Na koordinatnim osima u ponuđenom pravokutnom koordinatnom sustavu u ravnini već su ucrtane točke pridružene uređenim parovima, treba razmisliti kojem uređenom paru je pridružena koja točka.

Postupak:

Prvu koordinatu uređenog para pronalazimo na osi $x,$ a drugu na osi $y .$ Ako je prva koordinata $0,$ točka se nalazi na osi $y,$ a ako je druga koordinata $0$ točka se nalazi na osi $x .$

Zaključimo.

Točke na osi $x$ imaju

jednaku

0 .

Točke na osi

x

su oblika

. Točke na

imaju

jednaku

0 .

Točke na osi

y

su oblika

. Točka kojoj su i apcsisa i ordinata jednake

0

pripada i osi

x

i osi

y

i zove se

. Ishodište je točka

T (x, 0)

O (0, 0)

T (0, y)

ishodište

osi

y

apscisu

ordinatu

Pomoć:

Dopuni rečenice tako da imaju smisla.

Postupak:

Dobro pogledaj prethodni zadatak i razmisli.

Zadatak 10.

Ucrtaj u pravokutni koordinatni sustav točke $A (0, - 1),$ $B (- 4, - 2),$ $C (2, 0),$ $D (2, - 3)$ i $E (- 3, 0) .$ Pokušaj u bilježnicu samostalno riješiti zadatak, zatim usporedi svoje rješenje s ponuđenim.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke A, B, C, D i E pridružene uređenim parovima. — Točke u pravokutnom koordinatnom sustavu u ravnini

Zadatak 11.

Razmisli i odgovori.

Točka $A (0, - 5)$ nalazi se

Točka

B (4, 0)

nalazi se

Točka

C (- 6, 0)

nalazi se

Pomoć:

Ucrtaj točke u pravokutni koordinatni sustav u ravnini i odredi položaj zadane točke.

Postupak:

Ako je apscisa $0,$ točka se nalazi na osi $y,$ a ako je ordinata $0$ točka se nalazi na osi $x .$

Zadatak 12.

Odredi koordinate točaka $A,$ $B,$ $C$ i $O$ sa slike. Spoji parove.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke A, B, C i O.

$B$	$(2, - 2)$
$O$	$(3, 0)$
$A$	$(- 3, 4)$
$C$	$(0, 0)$

Pomoć:

Dobro pogledaj položaj točaka u pravokutnom koordinatnom sustavu u ravnini i razmisli.

Postupak:

Apscisu očitamo na osi $x,$ a ordinatu na osi $y .$

Točke i kvadranti

Zanimljivost

Riječ kvadrant dolazi od latinske riječi quadrans što znači četvrtina.

Pravokutni koordinatni sustav dijeli ravninu na četiri kvadranta, kako smo već ranije zaključili. Kvadrante označavamo rednim brojevima. Gornji desni dio ravnine označen je kao prvi kvadrant. Ostali kvadranti su označeni u smjeru obrnutom od kretanja kazaljke na satu.

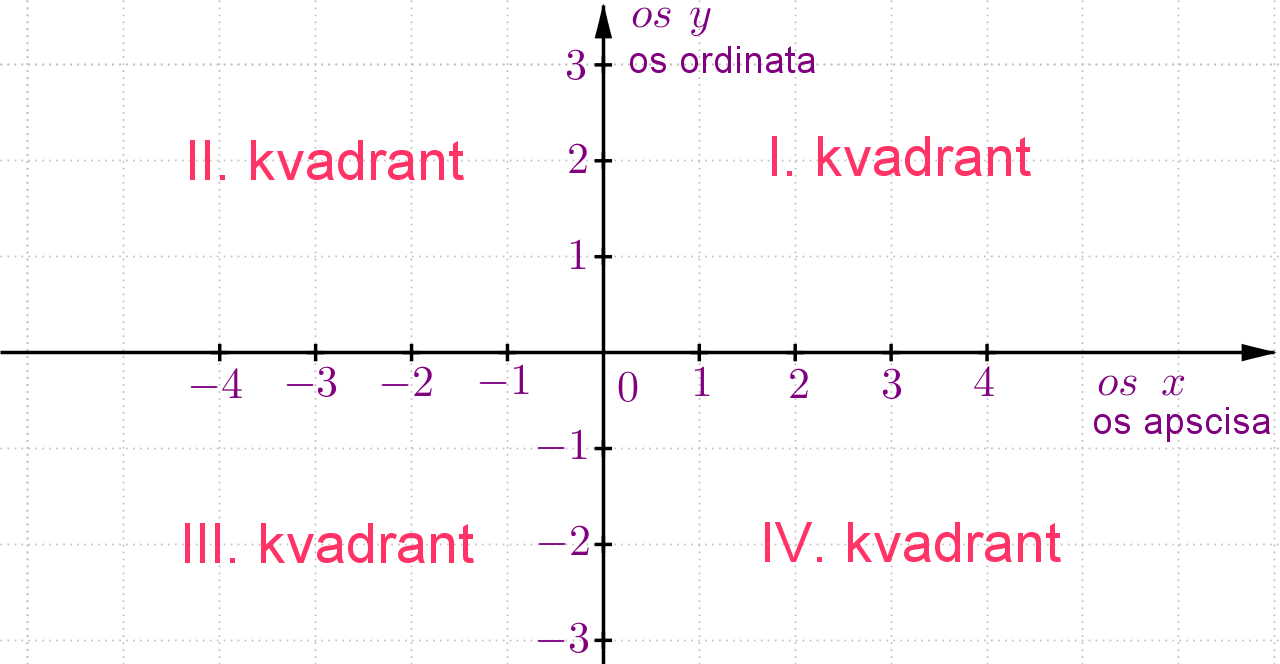
Četiri kvadranta u pravokutnom koordinatnom sustavu. — Kvadranti

Zadatak 13.

Odredi kvadrant u kojem se nalaze točke

A,

B,

C

D

sa slike.

U pravokutnom koordinatnom sustavu u ravnini ucrtane su točke A, B, C i D sa svojim koordinatama.

Točka $A (- 4, - 2)$ nalazi se u
Točka $B (4, 3)$ nalazi se u
Točka $C (- 3, 1)$ nalazi se u
Točka $D (2, - 3)$ nalazi se u

Pomoć:

Dobro pogledaj položaj točaka u pravokutnom koordinatnom sustavu u ravnini i razmisli.

Zaključimo.

Ako su predznaci koordinata točke

točka se nalazi u I. kvadrantu . Točka s predznacima koordinata

nalazi se u II. kvadrantu. Ako su predznaci koordinata točke

točka je u III. kvadrantu

,

a ako su predznaci koordinata točke

ona se nalazi u IV. kvadrantu.

(-, +)

(+, -)

(-, -)

(+, +)

Pomoć:

Dopuni rečenice tako da imaju smisla.

Postupak:

Dobro pogledaj položaj točaka u pravokutnom koordinatnom sustavu u ravnini i razmisli.

Zadatak 14.

Razvrstaj točke po kvadrantima.

A (- 4, 7)

H (- 1, 1)

J (- 8, 3)

G (- 6, 2)

C (- 4, - 9)

I (6, - 5)

D (3, - 3)

F (8, - 7)

E (- 7, - 3)

B (3, 5)

I. kvadrant

II. kvadrant

III. kvadrant

IV. kvadrant

Pomoć:

Dobro pogledaj koordinate točaka i razmisli.

Postupak:

Nacrtaj u bilježnici točke u pravokutnom koordinatnom sustavu u ravnini i odredi kojem kvadrantu pripada pojedina točka.

Zadatak 15.

Odredi bez crtanja pravokutnog koordinatnog sustava u ravnini kojem kvadrantu ili koordinatnoj osi pripada pojedina točka.

Točka $(0, - 17)$ se nalazi
Točka $(- 345, 11)$ se nalazi
Točka $(- 23, - 54)$ nalazi se
Točka $(15, 0)$ nalazi se
Točka $(72, 567)$ nalazi se
Točka $(14, - 28)$ nalazi se

Pomoć:

Dobro pogledaj koordinate točaka i razmisli.

Postupak:

Točka oblika $(0, y)$ nalazi se na osi $y,$ točka oblika $(x, 0)$ nalazi se na osi $x,$ točka oblika $(+, +)$ nalazi se u I. kvadrantu, točka oblika $(-, +)$ nalazi se u II. kvadrantu, točka oblika $(-, -)$ nalazi se u III. kvadrantu, a točka oblika $(+, -)$ nalazi se u IV. kvadrantu.

...i na kraju

Za kraj se poigraj interakcijom u GeoGebri. Dobit ćeš zanimljive sličice u pravokutnom koordinatnom sustavu.

Smisli i ti neki lik te ga nacrtaj u pravokutnom koordinatnom sustavu u ravnini i očitaj njegove koordinate. Uradak možeš napraviti u bilježnici ili u GeoGebri.

$A (2, - 3),$ $B (- 2, 5)$	$P (- 2, - 3)$
$A (4, 3),$ $B (- 4, - 3)$	$P (- 3, 3)$
$A (- 2, - 1),$ $B (- 4, 7)$	$P (0, 1)$
$A (4, - 3),$ $B (- 8, - 3)$	$P (0, 0)$

Na početku...

Pravokutni koordinatni sustav u ravnini

Zanimljivost

Zadatak 1.

Zanimljivost

Uređeni parovi i koordinate točaka u pravokutnom koordinatnom sustavu u ravnini

Primjer 1.

Koordinate točke u pravokutnom koordinatnom sustavu

Zadatak 2.

Točke u pravokutnom koordinatnom sustavu u ravnini

Zadatak 3.

Zadatak 4.

Zadatak 5.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Točke na koordinatnim osima

Zadatak 9.

Zadatak 10.

Zadatak 11.

Zadatak 12.

Točke i kvadranti

Zanimljivost

Zadatak 13.

Zadatak 14.

I. kvadrant

II. kvadrant

III. kvadrant

IV. kvadrant

Zadatak 15.

Simetrije u pravokutnom koordinatnom sustavu u ravnini

Primjer 2.

Primjer 3.

Primjer 4.

Kolekcija zadataka #1

Praktična vježba

Kutak za znatiželjne

Polovište dužine u pravokutnom koordinatnom sustavu u ravnini

Polovište dužine u pravokutnom koordinatnom sustavu

Zadatak 16.

...i na kraju