

Za ovaj zadatak nije odmah vidljiva računska radnja. Da bismo saznali cijenu jedne kuglice, moramo zadatak prvo matematički zapisati. Nakon toga razmislimo kojim bismo računskim radnjama mogli saznati cijenu. Na kraju trebamo provjeriti ima li dobiveno rješenje smisla.
Za razliku od algebarskih izraza u problemu sa sladoledom znamo koliko Filip ima novaca na početku pa problem možemo zapisati u obliku jednakosti. Odaberi točnu jednakost.
Pomoć:
Cijenu kuglice označi slovom
Postupak:
Zapiši izraz kojim opisuješ da od broja
oduzimaš trostruki broj
i ostane ti
Za rješenje problema moramo prvo izračunati razliku ukupne svote i količine novca koja je ostala Filipu,
Pomoć:
Dobro pogledaj matematički izraz i razmisli.
Postupak:
Prvo treba saznati koji broj treba oduzeti od da se dobije Zatim treba razmisliti koji broj pomnožen s daje tu razliku.
Cijena jedne kuglice je
Pomoć:
Rješenje pomnoži s
oduzmi od
i ako dobiješ
rješenje je dobro.
Postupak:
Ako pogledamo matematički zapis problema sa sladoledom, vidimo da s lijeve i s desne strane jednakosti imamo algebarske izraze.
Jednadžba
Matematički zapis u kojem imamo s lijeve i s desne strane jednakosti algebarske izraze zovemo jednadžba.
U animaciji pogledaj neke vrste jednadžbi.
Za sada ćemo se baviti samo linearnim jednadžbama.
Razvrstaj zadane jednadžbe.
Pomoć:
Pogledaj dobro animaciju i prepoznaj linearne jednadžbe među ponuđenima.
U jednadžbama imamo slova čiju vrijednost moramo otkriti matematičkim postupcima.
Nepoznanica
Nepoznati broj označen slovom u jednadžbi čiju vrijednost moramo otkriti matematičkim postupcima zovemo nepoznanica.
Jednadžbe mogu imati jednu ili više nepoznanica.
Isto slovo u jednoj jednadžbi predstavlja istu nepoznanicu. Ako imamo više različitih slova, onda imamo i više nepoznanica u jednadžbi.
Razvrstaj jednadžbe po broju nepoznanica.
Pomoć:
Isto slovo znači istu nepoznanicu. Ako su u jednadžbi dva ili više različitih slova, onda je to jednadžba s više nepoznanica.
Postupak:
Ako piše na više mjesta slovo
i nema ni jednog drugog slova u jednadžbi, onda je to jednadžba s jednom nepoznanicom.
Zaključimo.
Linearna jednadžba s jednom nepoznanicom
Linearna jednadžba s jednom nepoznanicom je jednadžba oblika gdje su i zadani brojevi.
Prisjetimo se matematičkog zapisa algebarskih izraza.
Zadane rečenice zapiši u obliku algebarskog izraza. Odaberi točan zapis.
| Broj za veći od | |
| Broj uvećaj puta. | |
| Broj umanji za | |
| Broj koji je puta manji od |
Pomoć:
Dobro pročitaj rečenice i zapiši ih u obliku algebarskog izraza.
Postupak:
Uvećati za neki broj znači zbrajanje, umanjiti za neki broj znači oduzimanje. Uvećati nekoliko puta znači množenje, umanjiti nekoliko puta znači dijeljenje.
Razmisli.
Odaberi riječi koje u rečenici
znače jednakost.
Pomoć:
Rečenicu treba pročitati s razumijevanjem.
Postupak:
Riječi koje u rečenici znače jednakost su jednako je, je, daje, dobit ćemo, dobit ćeš, postaje, bit će i tome slično.
Riječi koje u rečenici znače jednakost označavaju da se radi o jednadžbi. Pokušaj zapisati sljedeće rečenice kao linearne jednadžbe.
Spoji parove rečenica i njihov zapis s pomoću linearnih jednadžbi.
|
Broj
umanjen
puta daje
|
|
|
Broj
uvećan za
daje
|
|
|
Ako broj
umanjimo za neki broj, dobit ćemo
|
|
|
Broj koji je
puta veći od
jednak je
|
Pomoć:
Dobro pročitaj zadatak i razmisli o matematičkom zapisu.
Postupak:
Uvećati za znači zbrajanje, uvećati nekoliko puta znači množenje, umanjiti za znači oduzimanje, umanjiti nekoliko puta znači dijeljenje. Dijeljenje možemo zapisati u obliku razlomka.
U sljedećim zadatcima rečenice zapiši linearnom jednadžbom.
Za zadanu linearnu jednadžbu
smisli rečenicu. Možete se u razredu dogovoriti i svatko zadati jednu linearnu jednadžbu, a ostali učenici trebaju smisliti rečenice za tu linearnu jednadžbu. Najzanimljivije rečenice stavite na pano i neka učenici iz drugih razreda zapišu linearne jednadžbe za njih.
Prisjetimo se zadatka sa sladoledom s početka jedinice.
U zadatku sa sladoledom Filip je na početku imao
Pomoć:
Pogledaj zadatak na početku ove jedinice.
Za linearnu jednadžbu
Pomoć:
Zamijeni slovo
brojem
u zadanoj linearnoj jednadžbi.
Uvrsti broj koji daje točno rješenje linearne jednadžbe tako da ga dovučeš na mjesto nepoznanice
na slici.
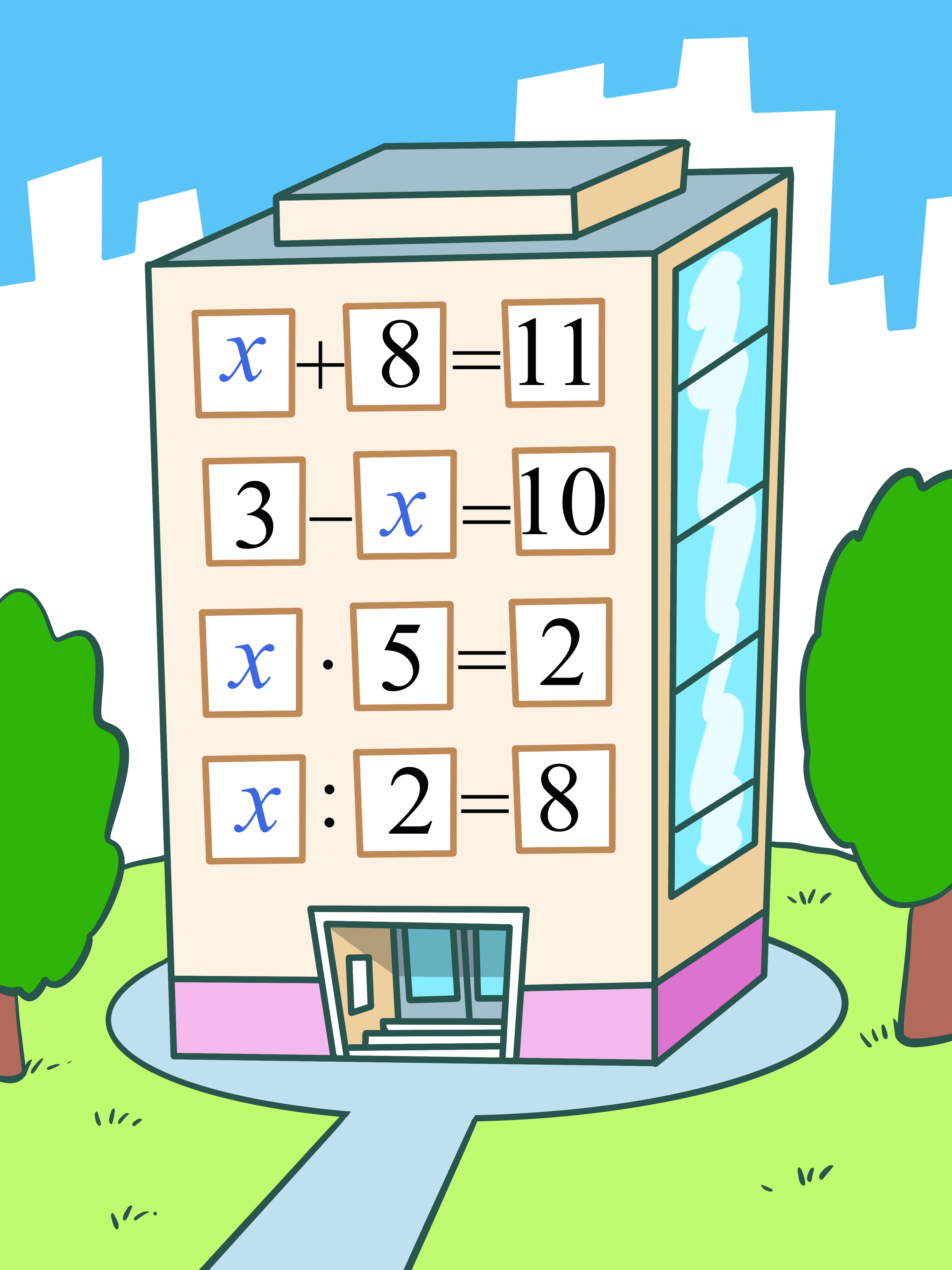
Pomoć:
U bilježnici ili napamet uvrsti broj umjesto
u linearnu jednadžbu i provjeri istinitost jednakosti.
Zaključimo.
Rješenje linearne jednadžbe
Rješenje linearne jednadžbe je broj koji pri uvrštavanju umjesto nepoznanice daje istinitu jednakost.
Primjer 1.
Provjeri je li broj rješenje linearne jednadžbe Pravilan postupak provjere pogledaj u rješenju primjera.
Da bismo provjerili je li neki broj rješenje linearne jednadžbe, moramo ga uvrstiti umjesto nepoznanice. Pritom prepisujemo sve ostale brojeve i računske radnje u jednadžbi i to s obiju strana jednadžbe.
Broj
je rješenje zadane linearne jednadžbe.
Primjer 2.
Provjeri je li broj rješenje linearne jednadžbe Zadatak riješi u bilježnicu postupkom iz prethodnog primjera, a zatim svoj zaključak provjeri u ponuđenom rješenju.
Uvrsti broj umjesto u zadanu jednadžbu.
Jednakost nije istinita pa kažemo da broj
nije rješenje zadane linearne jednadžbe.
Uvježbajmo.
Na prvi se pogled čini da svaka linearna jednadžba s jednom nepoznanicom ima jedno rješenje. No, je li to baš tako, istraži u sljedećim zadatcima.
Istražimo
Ispitaj koji je od ponuđenih brojeva rješenje jednadžbe
Označi sve koji to jesu.
Pomoć:
Uvrsti svaki broj i za svaki napravi provjeru linearne jednadžbe.
Postupak:
1.
2.
3.
4.
5.
6.
Za zadanu jednadžbu smisli još neki broj. Uvrsti taj broj i uvjeri se da je i on rješenje zadane linearne jednadžbe.
Za linearnu jednadžbu
kažemo da ima beskonačno mnogo rješenja.
Za linearnu jednadžbu
Pomoć:
Prisjetimo se svojstva množenja brojeva s nulom.
Postupak:
Kada bilo koji broj množimo s
rješenje je uvijek
Za bilo koji broj koji uvrstimo umjesto
ne možemo dobiti istinitu jednakost.
Za linearnu jednadžbu
kažemo da nema rješenja.
Zaključimo.
Linearna jednadžba s jednom nepoznanicom može imati točno jedno rješenje, može imati beskonačno mnogo rješenja ili može biti takva da nema ni jedno rješenje.
Pokušaj napamet izraziti nepoznate veličine pazeći na vezu između računskih radnji.
Ako nismo sigurni koju računsku radnju odabrati da bismo izrazili nepoznatu veličinu iz jednostavne linearne jednadžbe, možemo si pomoći jednostavnim brojevnim izrazima. Takvi izrazi su npr.
ili
Označimo broj koji se nalazi na mjestu nepoznate veličine i razmislimo kojom računskom radnjom bismo izračunali taj označeni broj pomoću preostalih brojeva iz brojevnog izraza.
Izrazi nepoznate veličine iz matematičkih izraza i nekih poznatih formula koristeći se vezom računskih radnji.
Izrazi veličinu
iz algebarskog izraza ako su
Spoji parove.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Zamisli da su umjesto
i
brojevi.
Postupak:
Razmisli kojom bismo računskom radnjom saznali broj koji se nalazi na mjestu
u izrazu.
Izrazi veličinu iz algebarskog izraza ako su Spoji parove.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Zamisli da su umjesto i brojevi.
Postupak:
Razmisli kojom bismo računskom radnjom saznali broj koji se nalazi na mjestu u izrazu.
Izrazi veličinu iz formule za opseg ili površinu ako su i pozitivni racionalni brojevi. Spoji parove.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Zamisli da su umjesto slova u formulama brojevi.
Postupak:
Razmisli kojom bismo računskom radnjom saznali broj koji se nalazi na mjestu u formuli.
Prisjeti se još nekih formula i izrazi nepoznate veličine iz tih formula koristeći se vezom između računskih radnji.
Odigraj igru memory s prijateljima. U igri se nalazi
kartica. Na 6 se kartica nalaze linearne jednadžbe, a na 6 se kartica nalaze rješenja tih linearnih jednadžbi. Kartice su okrenute naopako da se ne vidi što piše. Igrači redom okreću po dvije kartice. Treba spojiti par kartica na kojima su linearna jednadžba i njezino rješenje. Ako ne možeš napamet odgonetnuti je li broj na otkrivenoj kartici rješenje linearne jednadžbe na drugoj otkrivenoj kartici, napravi provjeru u bilježnici. Igra je gotova kada su spojeni svi parovi. Pobjednik u igri je onaj tko skupi najviše parova.