

Četverokut je dio ravnine omeđen četirima dužinama, uključujući i točke koje pripadaju tim dužinama. Četverokut ima četiri vrha i četiri kuta. Dužine koje omeđuju četverokut nazivaju se stranice četverokuta.
Otprije znaš pravilno označiti trokut. Za označavanje vrhova i veličina kutova četverokuta vrijede ista pravila kao za trokut. Za označavanje veličina stranica postoji drukčije pravilo.
Vrhove i veličine kutova četverokuta označit ćemo kao i ranije.
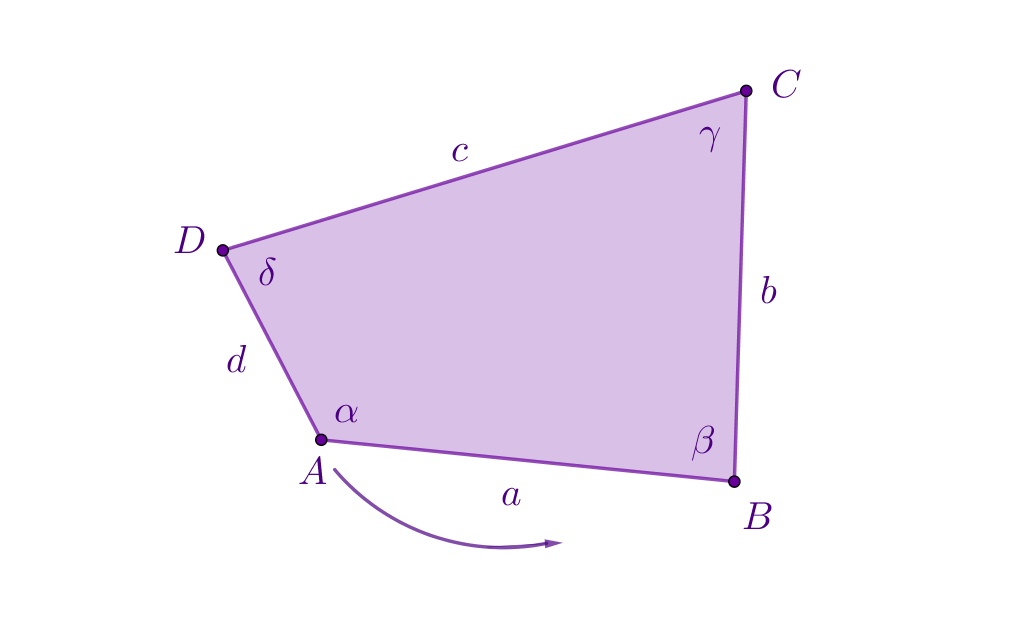
Označimo bilo koji vrh s i veličinu pripadnog unutarnjeg kuta četverokuta s Preostale vrhove i pripadne veličine unutarnjih kutova i te i označit ćemo u smjeru obrnutom od kretanja kazaljke sata.
Za duljine stranica vrijedi:
Uvježbajmo.
Ponovimo.
Pomoć:
Pomoć potraži u jedinici 2.3. Svojstva trokuta.
Postoji li slična veza i za veličine unutarnjih kutova četverokuta?
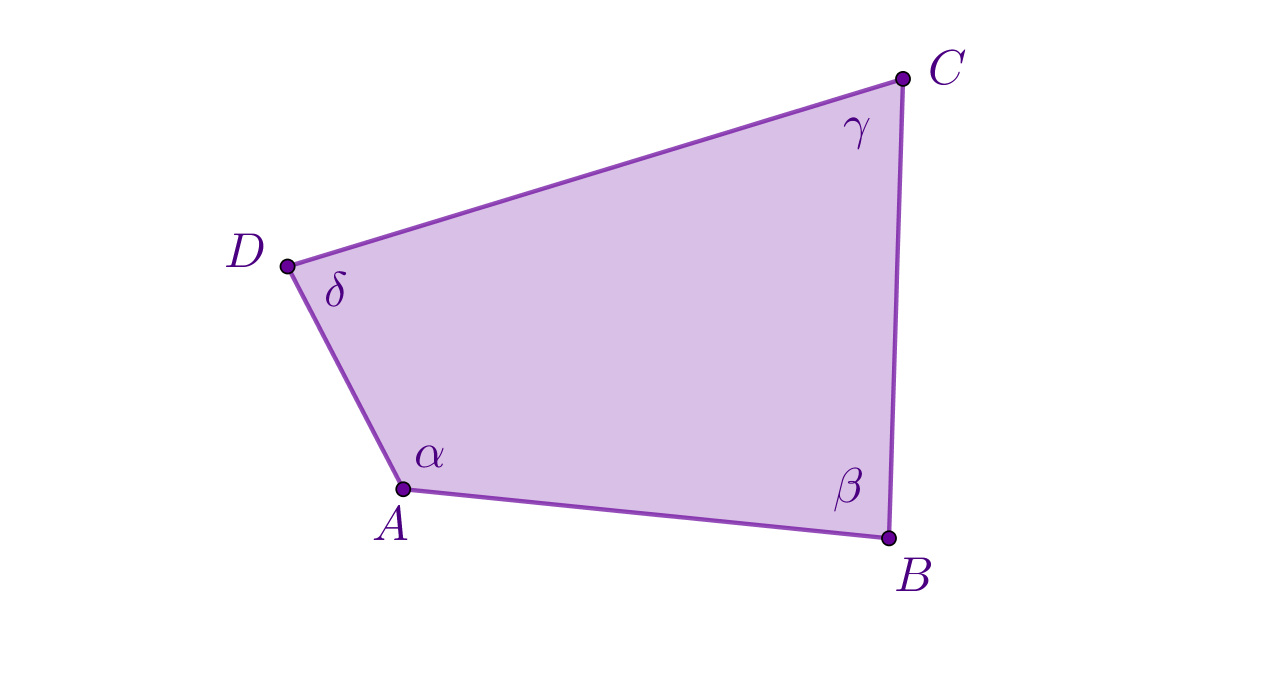
Pažljivo pogledaj animaciju koja slijedi jer osim što daje odgovor na prethodno pitanje, i dokazuje ga.
Zbroj veličina unutarnjih kutova četverokuta
Zbroj veličina unutarnjih kutova svakog četverokuta iznosi
Nacrtaj u bilježnicu bilo koji četverokut i izmjeri kutomjerom veličine unutarnjih kutova tog četverokuta. Zbroji veličine kutova.
Ako je mjerenje bilo precizno, zbroj iznosi
Ako mjerenje nije bilo precizno, dobiveni zbroj odstupa nekoliko stupnjeva od
Ako je odstupanje veliko, vjerojatno ne upotrebljavaš kutomjer na pravilan način pa potraži pomoć.
Pokus
- nacrtaj četverokut
- unutarnje kutove oboji različitim bojama
- odreži ili pažljivo otkini svaki kut četverokuta (u obliku kružnog isječka)
- složi kutove jedan do drugoga na način da se vrhovi podudaraju
- uoči da kutovi zatvaraju puni kut ( ).
Dokaži da je zbroj veličina vanjskih kutova svakog četverokuta
Ako nemaš ideju kako započeti dokaz, prisjeti se načina dokazivanja tvrdnje o zbroju veličina vanjskih kutova trokuta.
Četverokute možemo razvrstati s obzirom na paralelnost stranica.
Postoje četverokuti koji imaju točno jedan par paralelnih stranica, oni koji imaju dva para paralelnih stranica i oni koji nemaju paralelnih stranica.
Dalje ćemo proučavati četverokute čija su dva para stranica međusobno paralelna.
Četverokut kojemu su nasuprotne stranice paralelne naziva se paralelogram.
Istražimo
U GeoGebrinu apletu dan je paralelogram kojemu povlačenjem vrhova i možeš mijenjati duljine stranica i veličine kutova koje zatvaraju susjedne stranice.
Prati promjene koje se događaju.
Izvedi zaključke.
(svojstva paralelograma: kutovi, stranice)
Provjeri svoja zapažanja u sljedećim zadatcima.
Po potrebi, ponovno se vrati na aplet i preispitaj zaključak.
Slika prikazuje vrste parelelograma.
Prouči i odgovori na pitanja.
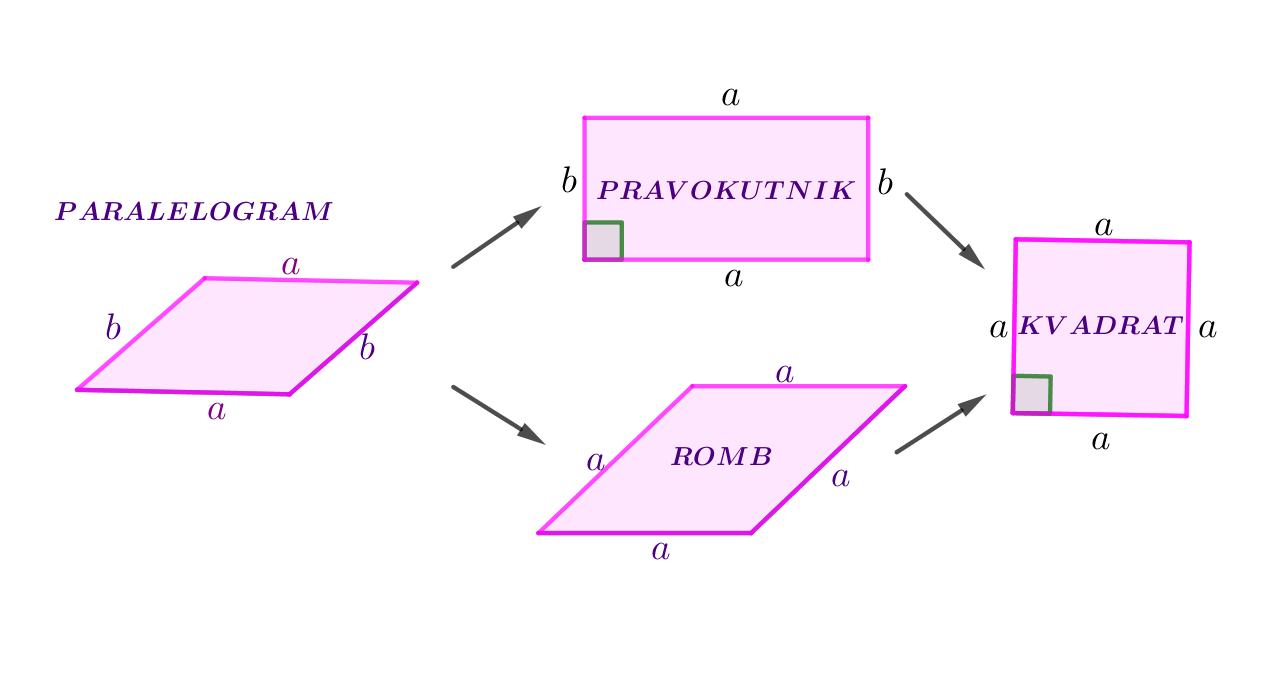
Romb je
Pomoć:
Prouči još jednom danu sliku.
Istražimo
U GeoGebrinu apletu dan je paralelogram kojemu možeš povlačenjem vrhova mijenjati duljine stranica i veličine kutova koje zatvaraju susjedne stranice.
Točka sjecište je dijagonala paralelograma, a istaknut je i kut koji te dijagonale zatvaraju.
Pomiči vrhove i prati nastale promjene. Što zaključuješ?
Pomicanjem vrhova nactaj sve vrste paralelograma i provjeri svoje zaključke.
Provjeri svoja zapažanja u sljedećim zadatcima.
Po potrebi, ponovno prouči aplet i preispitaj zaključak.
Pravokutnik je paralelogram kojemu su svi kutovi pravi.
Kvadrat je pravokutnik kojemu su sve stranice jednakih duljina.
Romb je paralelogram kojemu su sve stranice jednakih duljina.