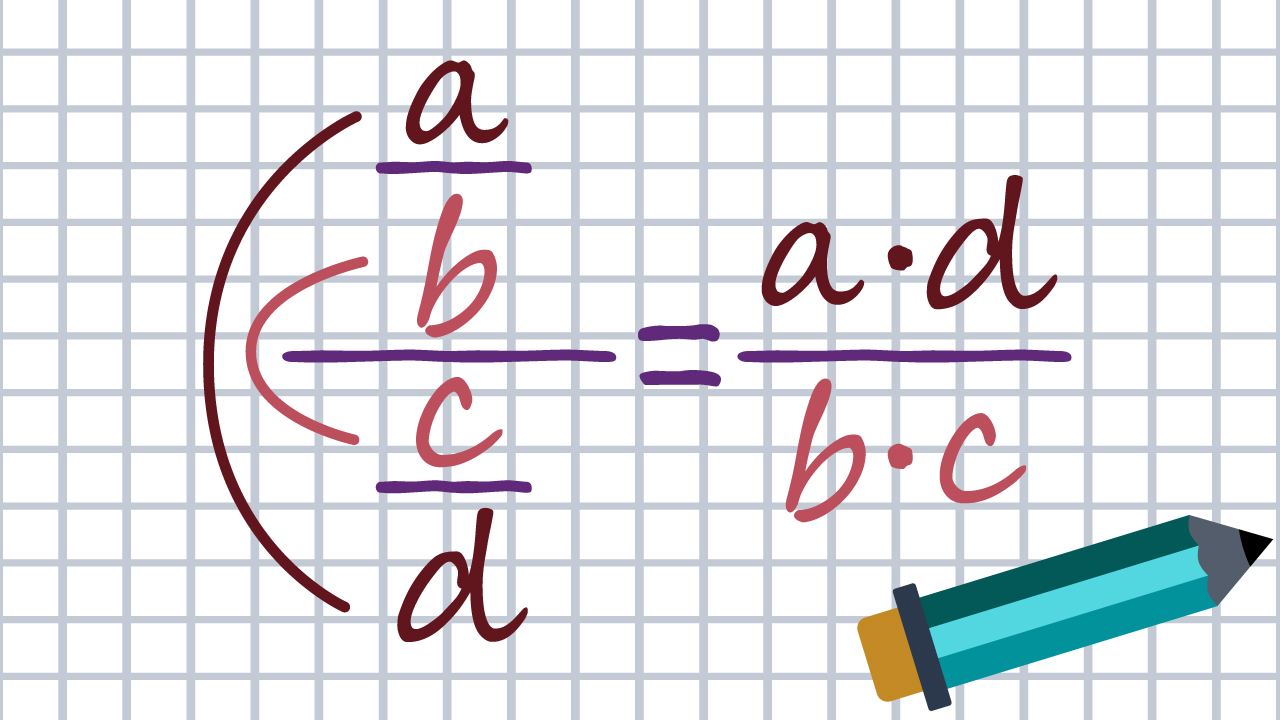


Nakon kratkog ponavljanja istraži kakvi su to dvojni i verižni razlomci te riješi nekoliko problemskih zadataka. Znatiželjni mogu pokušati riješiti i jednostavne algebarske razlomke. Za kraj, riješi križaljku matematičkih pojmova.
Rješavanjem zadataka ponovi osnovno o računanju s razlomcima.
Dobivena rješenja i postupke usporedi i raspravi s prijateljima. Podijeli svoje znanje s njima ili, ako trebaš, zatraži pomoć.
Istražimo
Razmisli i pokušaj izračunati vrijednost dvojnog razlomka Najprije pokušaj samostalno, a zatim, provjeri svoja razmišljanja u rješenju.
Razlomačka crta znači dijeljenje. Kao što vidimo iz zadatka, dvojni razlomak je razlomak koji u brojniku i nazivniku također ima razlomke. Podijelimo ih.
Razmisli, dopuni rečenicu i poredaj korake rješavanja dvojnog razlomka po redu.
Dvojni razlomak je
Pomoć:
Dopuni rečenicu tako da ima smisla.
Dvojni razlomak oblika
rješavamo tako da podijelimo brojnik s nazivnikom. Poredaj korake po redoslijedu rješavanja.
Pomoć:
Razlomačka crta znači dijeljenje.
Postupak:
Razlomke dijelimo tako da dijeljenik pomnožimo s recipročnim djeliteljem.
Zaključi i na kartici provjeri kako možemo kraće riješiti dvojni razlomak.
Uvježbaj rješavanje jednostavnih dvojnih razlomaka.
Verižni razlomak je razlomak koji se zapisuje u obliku zbroja cijelog broja i razlomka koji u nazivniku ima zbroj cijelog broja i razlomka koji, opet, u nazivniku ima zbroj cijelog broja i razlomka i tako dalje. Verižni razlomak može biti konačan i beskonačan. Svaki racionalni broj može se zapisati u obliku konačnog verižnog razlomka. Ti razlomci imaju primjenu u rješavanju jednadžbi, a matematičari se njima bave još od Euklida (300 g. pr. Kr.).
Razmisli i pokušaj samostalno riješiti verižni razlomak
U ponuđenom rješenju zadatka provjeri svoja razmišljanja, točnost postupka i konačnu vrijednost zadanog verižnog razlomka.
Kod ovakvih zadataka treba pisati uredno i pregledno. Zadatak se rješava "odozdo prema gore", poštujući redoslijed računskih radnji. Pritom, razlomačka crta odvaja računske radnje kao i zagrada.
Izračunaj vrijednost verižnog razlomka
Složite se u grupe i zadajte si međusobno još nekoliko verižnih razlomaka te ih riješite. Ako ste spremni na još veće izazove, probajte ići obrnutim redom i neki razlomak
prikažite kao verižni razlomak
(primjerice
).
Sve svoje uratke prikažite prezentacijom pred cijelim razredom ili napravite izložbu na razrednom ili školskom panou.
Roditelji zarađuju
kn mjesečno i za račune odvajaju
primanja,
primanja odvajaju za otplatu stambenog kredita,
izdvajaju za hranu i higijenske potrepštine,
za prijevoz. Izračunaj koliko toj obitelji mjesečno ostane za ostale troškove. Mogu li mjesečno nešto novca staviti sa strane i uštedjeti?
Mjesečno obitelj za račune potroši
kn, za otplatu kredita izdvoji
kn,
kn potroše na hranu i potrepštine, te
kn na prijevoz. Ostane im
kn, pa mogu malo i uštedjeti, ako žele.
Pitajte u svojoj obitelji kolika su im primanja, koliki su redoviti mjesečni troškovi i razgovarajte o mogućoj štednji. Na satu razrednika ili matematike možete razgovarati o toj temi, ali nemojte javno iznositi primanja i troškove svoje obitelji. Možete se podijeliti u grupe i izračunati prosječna primanja obitelji unutar vaše grupe, prosječne redovne mjesečne troškove i izračunati koliko prosječno ostaje za ostale troškove. Da ne biste javno iznosili primanja i troškove napišite iznose na papiriće i stavite u jednu kutijicu iz koje ćete nasumično vaditi podatke. Usporedite podatke svih grupa.
U jednom dućanu sa cipelama su ponudili popust pri plaćanju u sljedećem obliku: ako kupiš jedan par cipela, popust je
ako kupiš dva para popust na ukupan iznos je
a ako kupiš tri para cipela, popust na ukupan iznos je
Katarini se sviđaju troje cipele čije su cijene
kn,
kn i
kn. Pomozi joj izračunati koliko bi uštedjela ako kupi samo jedne cipele po
kn, koliko ako kupi dvoje po
kn i
kn, ili sve troje.
od
kn je
kn, znači, pri kupnji jednih cipela od
kn, uštedjela bi
kn. Ako kupi dvoje cipele po cijeni od
kn i
kn, ušteda bi bila
kn, a ako kupi sve troje cipele uštedjela bi
kn.
Izračunaj uštede u svim kombinacijama kupnje jednog ili dva para tih cipela. Primjerice, koliko bi uštedjela ako kupi samo cipele čija je cijena
kn, a koliko kupi li jedne cipele po cijeni od
kn, a druge po cijeni od
kn. Izračunaj uštede i za sve ostale kombinacije.
Baršun, brokat i til su vrste tkanina. Ako te zanima više o tkaninama i šivanju, možeš pogledati ovdje.
Krojač naručuje tkaninu za kostime u kazalištu. Naručio je
crvenog baršuna po cijeni
kn po metru određene širine,
zlatnog brokata po cijeni
kn po metru iste širine te
bijelog tila po cijeni
kn po metru uobičajene širine. Koliko je platio cijelu narudžbu, ako je još dobio
popusta na ukupnu cijenu narudžbe?
Cijena ukupne narudžbe je
kn.
Iznos popusta je
kn,
a konačna cijena s tim popustom je
kn.
Pokušaj pojednostaviti nekoliko algebarskih razlomaka. To su razlomci koji u brojniku ili nazivniku imaju algebarske izraze. S algebarskim razlomcima računamo isto kao i s običnim razlomcima.
Za kraj, riješi križaljku matematičkih pojmova. U označenim poljima dobit ćeš još jedan pojam.