Definicija niza

U matematici ćemo promatrati nizove realnih brojeva. Niz realnih brojeva dobit ćemo kada neke brojeve poredamo po određenom redu, nanižemo. Za svaki broj možemo reći koji je po redu u tom nizu, odnosno koji je njegov redni broj.

Primjer 1.

Promotrite niz brojeva: $2,$ $7,$ $11,$ $34,$ $12,$ $25,$ $15,$ $19,$ $7 .$ Koji je broj peti po redu? Koji je po redu broj $11 ?$ A koji je po redu broj $7 ?$

Peti je broj $12,$ broj $11$ je treći, a $7$ drugi i deveti.

Pogledajmo kako ćemo preciznije, matematičkim jezikom, definirati niz.

Primjer 2.

Marko je tijekom školske godine deset puta bio ocijenjen iz matematike. Promotrite animaciju.

00:00

U Primjeru 2 promatrali smo niz od deset ocjena. Da bismo opisali koja je po redu neka od tih ocjena, trebao nam je skup $\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} .$ Mi ćemo često promatrati beskonačne nizove realnih brojeva. Da bismo opisali koji je po redu neki broj u beskonačnom nizu, trebat će nam skup prirodnih brojeva.

Niz realnih brojeva

Funkciju $a : N \to R$ zovemo niz realnih brojeva.

Broj $a (1)$ prvi je član niza. Označavamo ga kraće $a_{1} .$

Broj $a (2)$ drugi je član niza. Označavamo ga kraće $a_{2} .$

Broj $a (n)$ $n$ -ti je član niza. Označavamo ga kraće $a_{n}$ i zovemo opći član niza.

Niz $a$ označavamo $(a_{n}), n \in N .$

Zadatak 2.

Promotrite niz $a$ neparnih brojeva $1,$ $3,$ $5,$ $7,$ $9,$ $. . .$ pa riješite zadatke.

a. $a_{3} = 5$

Da

Ne

null

b. Označite točne odgovore.

$a_{9} = 9$

$a_{5} = 9$

$a_{9} = 5$

$a_{9} = 17$

null

Opisno zadani nizovi

Nizove možemo zadati opisom, na primjer niz svih neparnih prirodnih brojeva od najmanjeg prema većima.

Zadatak 3.

Niz $a$ je niz svih prostih brojeva od manjih prema većima. Odredite koji je član niza:

a. Peti član niza

$a$ je

.

null

b.

$a_{7} =$

.

null

Rekurzivno zadani nizovi

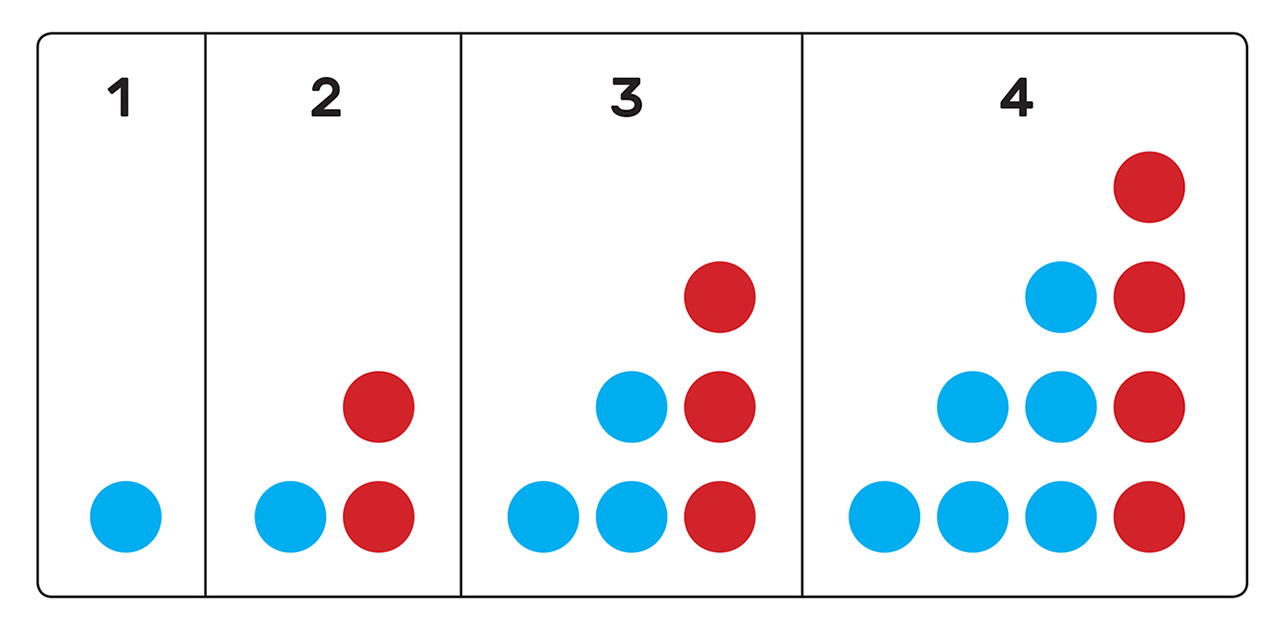
Na prvoj je slici jedan kružić, na drugoj slici su desno od tog jednog postavljena dva nova pa ih je ukupno tri. Na trećoj slici su desno od ta tri dodana još tri pa ih je ukupno šest. Na četvrtoj slici su desno od tih šest postavljena još četiri nova pa ih je ukupno deset. — Rekrurzivno zadani niz

Promotrite kružiće na slikama pa riješite zadatke.

Kolekcija zadataka #1

Na prvoj je slici prikazan

kružić.

Zapisujemo

$a_{1} = 1 .$

null

Na drugoj smo slici dodali

nova

kružića pa ih je ukupno

.

Zapisujemo

$a_{2} = a_{1} + 2 = 1 + 2 = 3 .$

null

Na trećoj smo slici dodali

nova kružića pa ih je ukupno

.

Zapisujemo

$a_{3} = a_{2} + 3 = 3 + 3 = 6 .$

null

Na četvrtoj smo slici dodali

nova

kružića pa ih je ukupno

. Zapisujemo

$a_{4} = a_{3} + 4 = 6 + 4 = 10 .$

null

Ako bismo nastavili crtati kružiće na isti način, koliko bismo kružića dodali na petoj slici? Koliko bi ih bilo ukupno na petoj slici? Kako biste to zapisali?

Na petoj bismo slici dodali pet kružića, ukupno bi ih bilo petnaest. Zapisujemo $a_{5} = a_{4} + 5 = 10 + 5 = 15 .$

Na desetoj slici bismo broju kružića na

slici

dodali

kružića.

Zapisujemo

$a_{10} = a_{9} + 10 .$

null

Na $n$ -toj slici bismo broju kružića na slici

dodali

kružić.

Zapisujemo

$a_{n} = a_{n - 1} + n .$

null

U prethodnom smo primjeru znali broj kružića na prvoj slici, a zatim smo broj kružića na nekoj slici računali pomoću broja kružića na prethodnoj slici. Matematičkim simbolima možemo zapisati: zadan je $a_{1}$ i $a_{n} = a_{n - 1} + n .$ Jasno je da na ovaj način možemo izračunati broj kružića na bilo kojoj slici. Kažemo da je niz zadan rekurzivno.

Rekurzivno zadani niz

Kažemo da je niz $a$ zadan rekurzivno ako je zadano nekoliko prvih članova i pravilo po kojemu se $a_{n}$ računa pomoću nekoliko prethodnih članova niza.

Zanimljivost

Predočavanje brojeva točkicama potječe od Babilonaca, a često su se tim načinom koristili Pitagorejci. Razlikovali su trokutaste, kvadratne, peterokutne i šesterokutne brojeve, a jednim su ih imenom nazivali figurativni brojevi. Trokutasti su brojevi $1,$ $3,$ $6,$ $10,$ ... jer se mogu prikazati točkicama raspoređenim u trokut. Kvadratni su brojevi $1,$ $4,$ $9,$ $16,$ ... jer se mogu prikazati točkicama raspoređenim u kvadrate. Tvrdnje vezane uz figurativne brojeve dokazivali su crtežima. Jedna od tvrdnji koje se na taj način mogu pokazati jest: Zbroj dvaju uzastopnih trokutastih brojeva je kvadratni broj. Nacrtajte sliku i provjerite.

Zadatak 4.

Niz je zadan rekurzivno: $a_{1} = 3,$ $a_{n} = 2 a_{n - 1} - 1 .$ Popunite tablicu u bilježnici.

$n$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$a_{n}$

$n$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$a_{n}$	$3$	$5$	$9$	$17$	$33$	$65$	$129$	$257$	$513$

Nizovi zadani formulom za opći član

Promotrimo ponovno primjer s kružićima. Kako biste izračunali koliko je kružića na stotoj slici? A na tisućitoj? Je li to jednostavno izračunati? Pronađimo lakši način.

Na prvoj slici su dva kružića, na drugoj slici ih je šest složenih u pravokutnik tri puta dva. Pravokutnik se sastoji od dva trokuta s po tri kuglice svaki. Na trećoj ih je dvanaest složenih u pravokutnik četiri puta tri. Pravokutnik se sastoji od dva trokuta s po šest kružića svaki. Na četvrtoj ih je dvadeset, složenih u pravokutnik pet puta četiri koji se sastoji od dva trokuta s po deset kružića svaki. — Niz zadan formulom za opći član

Zadatak 5.

Odredite broj kružića na prvoj, drugoj, trećoj i četvrtoj slici.

Na prvoj su dva kružića: $b_{1} = 2 .$

Na drugoj ih je šest: $b_{2} = 3 \cdot 2 = 6 .$

Na trećoj ih je dvanaest: $b_{3} = 4 \cdot 3 = 12 .$

Na četvrtoj ih je dvadeset: $b_{4} = 5 \cdot 4 = 20 .$

Zadatak 6.

Ako bismo nastavili crtati kružiće na isti način, koliko bi ih bilo na petoj slici? A na desetoj? Koliko bi ih bilo na stotoj? A na $n$ -toj? Zapišite odgovore matematičkim simbolima.

Na petoj bi bilo trideset kružića: $b_{5} = 6 \cdot 5 = 30 .$

Na desetoj bi ih bilo: $b_{10} = 11 \cdot 10 = 110 .$

Na stotoj bi ih bilo: $b_{100} = 101 \cdot 100 = 10 100 .$

Na $n$ -toj bi ih bilo: $b_{n} = (n + 1) \cdot n = n^{2} + n .$

Na prvoj je slici jedan kružić, na drugoj slici su desno od tog jednog postavljena dva nova pa ih je ukupno tri. Na trećoj slici su desno od ta tri postavljena još tri nova pa ih je ukupno šest. Na četvrtoj slici su desno od tih šest postavljena još četiri nova pa ih je ukupno deset. — Rekrurzivno zadani niz

Zadatak 7.

Usporedite nizove $a$ i $b$ koji predstavljaju broj kružića na slikama. Postoji li među njima neka veza? Izrazite $a_{n}$ pomoću $b_{n}$ i pomoću $n .$

$a_{n} = \frac{1}{2} b_{n} = \frac{(n + 1) n}{2}$

U prethodnim smo zadatcima niz odredili pomoću formule za opći član. Ako je zadana formula za opći član i redni broj člana, možemo lako izračunati traženi član. Ako je niz zadan rekurzivno, treba izračunati sve članove do traženog što za članove s velikim rednim brojem može biti zahtjevno.

Zadatak 8.

Neka je $a_{n} = n^{2} - 10 n .$ Izračunajte traženi član.

$a_{5} =$

.

null

$a_{105} =$

.

null

...i na kraju

Zadatak 9.

Razvrstajte nizove prema načinu na koji su zadani.

niz kvadrata prirodnih brojeva

Zadani opisno

Zadani rekurzivno

Zadani formulom za opći član

null

$a_{1} = 1,$ $a_{n} = a_{n - 1} + 2$	$a_{2} = 9$
zbroj prvih $n$ neparnih prirodnih brojeva	$a_{5} = 9$
$a_{n} = {(n + 1)}^{2}$	$a_{5} = 25$

$a_{5} = a_{4} +$	$99$
$a_{4} =$	$2 n - 1$
$a_{n} = a_{n - 1} +$	$16$
$a_{10} =$	$9$
$a_{50} = a_{49} +$	$100$
$a_{n} =$	$n^{2}$

2.1 Pojam niza

Na početku...

Zadatak 1.

Praktična vježba

Definicija niza

Primjer 1.

Primjer 2.

Niz realnih brojeva

Zadatak 2.

Opisno zadani nizovi

Zadatak 3.

Rekurzivno zadani nizovi

Kolekcija zadataka #1

Rekurzivno zadani niz

Zanimljivost

Zadatak 4.

Nizovi zadani formulom za opći član

Zadatak 5.

Zadatak 6.

Zadatak 7.

Zadatak 8.

...i na kraju

Zadatak 9.

Zadani opisno

Zadani rekurzivno

Zadani formulom za opći član

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: