Prisjetite se jednostavnog kamatnog računa. Koji su pojmovi vezani uz jednostavni kamatni račun? Riješite zadatke.
Jednostavni kamatni račun
Jednostavni kamatni račun primjenjujemo kad se kamate računaju na nepromijenjeni iznos glavnice. Kamate računamo po formuli:
pri čemu je iznos glavnice, godišnja kamatna stopa, vrijeme u godinama, a iznos kamata.
Istražimo
Tena je oročila kn na rok od godina uz kamatnu stopu od Kamate se na oročenu štednju svake godine obračunavaju i dodaju na glavnicu. Koliko će novca Tena imati na računu nakon pet godina? Riješite zadatke.
Primjer 1.
Iznos od kn oročen je na rok od godina uz kamatnu stopu od U prethodnom smo zadatku izračunali iznose na računu za svaku godinu te tako dobili iznos koji će biti na računu nakon pet godina. Možemo li računati brže?
Pogledajmo.
Označimo početni iznos s a s iznos na računu nakon godina.
Izračunajte iznos na računu nakon pet godina koristeći se formulom Jeste li dobili istu vrijednost kao u prethodnom zadatku? Što možete reći o nizu brojeva
Dobivamo istu vrijednost na oba načina. Niz brojeva je geometrijski s kvocijentom
Provedimo ovaj postupak općenito. Označimo:
– početni iznos
– godišnja kamatna stopa
– vrijeme u godinama
– iznos nakon
godina.
Neka se kamate obračunavaju po složenom kamatnom računu uz godišnju kamatnu stopu izraženu u postotcima. Početni iznos nakon godina narast će na iznos
Primjer 2.
Izračunajmo na koji će iznos narasti iznos od kn na kraju osme godine i kolike su ukupne kamate ako je godišnja kamatna stopa a obračun kamata godišnji. Koji su podatci zadani? Zadan je početni iznos
Treba izračunati
kn.
Ukupne su kamate razlika između iznosa na kraju osme godine i početnog iznosa:
kn.
Vratimo se na uvodni primjer koji sada znamo riješiti.
Roditelji žele oročiti kn dječje štednje na rok od godina. Banka nudi kamatnu stopu od a račun kamata je složen. Koliko će novca biti na računu nakon godina?
kn
Riješite zadatke.
Marko je uštedio
kn i želi kupiti električni bicikl. Cijena bicikla je
kn. Pronašao je banku koja za oročenu štednju nudi kamatnu stopu od
Na koliko bi godina morao oročiti svoju ušteđevinu?
Ušteđevinu bi morao oročiti na
godina.
Prepišite tablicu u bilježnicu, izračunajte vrijednosti koje nedostaju pa ih upišite u tablicu u bilježnici.
| Ukupne kamate | ||||
|---|---|---|---|---|
Što možete zaključiti na osnovi dobivenih vrijednosti u tablici?
| Ukupne kamate | ||||
|---|---|---|---|---|
U prethodnim se primjerima godišnja kamatna stopa pripisivala jedanput godišnje. Koristili smo se formulom za računanje iznosa nakon
godina:
Pripisivanje kamate može biti i polugodišnje, kvartalno ili mjesečno. U tom slučaju možemo se koristiti formulom
u kojoj je
godišnji broj pripisivanja kamate, a godišnja kamatna stopa
svedena je na odgovarajuću polugodišnju, kvartalnu ili mjesečnu. Pogledajmo na primjeru.
Iznos od
kn uložen je na
godina uz godišnju kamatnu stopu od
i složeni kamatni račun. Riješite zadatke.
U prethodnom smo zadatku računali iznose na računu nakon deset godina uz godišnje, polugodišnje, kvartalno i mjesečno ukamaćivanje.
U kojem smo slučaju dobili najveći iznos? Možemo pretpostaviti da su iznosi veći ako je ukamaćivanje češće.
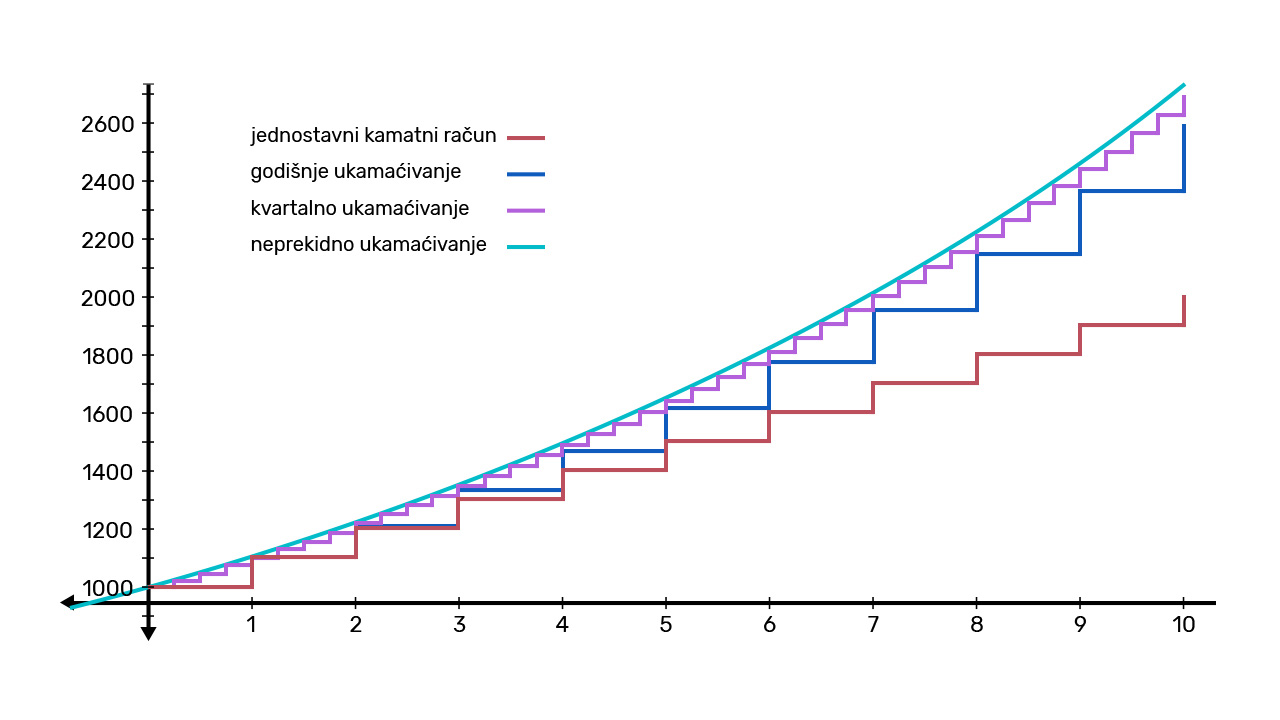
Promotrite sliku. Na slici su grafovi koji prikazuju iznos na računu u periodu od deset godina. Kamatna stopa je
a početna vrijednost (glavnica) je
kn.
Prvi graf prikazuje iznos pri jednostavnom kamatnom računu, drugi i treći pri složenom uz godišnje i kvartalno ukamaćivanje. Možete li pomoću grafova i u ovom slučaju potvrditi da su iznosi veći ako je ukamaćivanje češće?
Četvrti graf prikazuje neprekidno ukamaćivanje. Što je neprekidno ukamaćivanje proučit ćete u Aktivnostima za samostalno učenje.