


Tangenta u nekoj točki krivulje jest pravac koji u toj točki samo dodiruje tu krivulju. Pri tome pravac može sjeći krivulju u nekoj drugoj točki kao, primjerice, na sljedećoj slici.
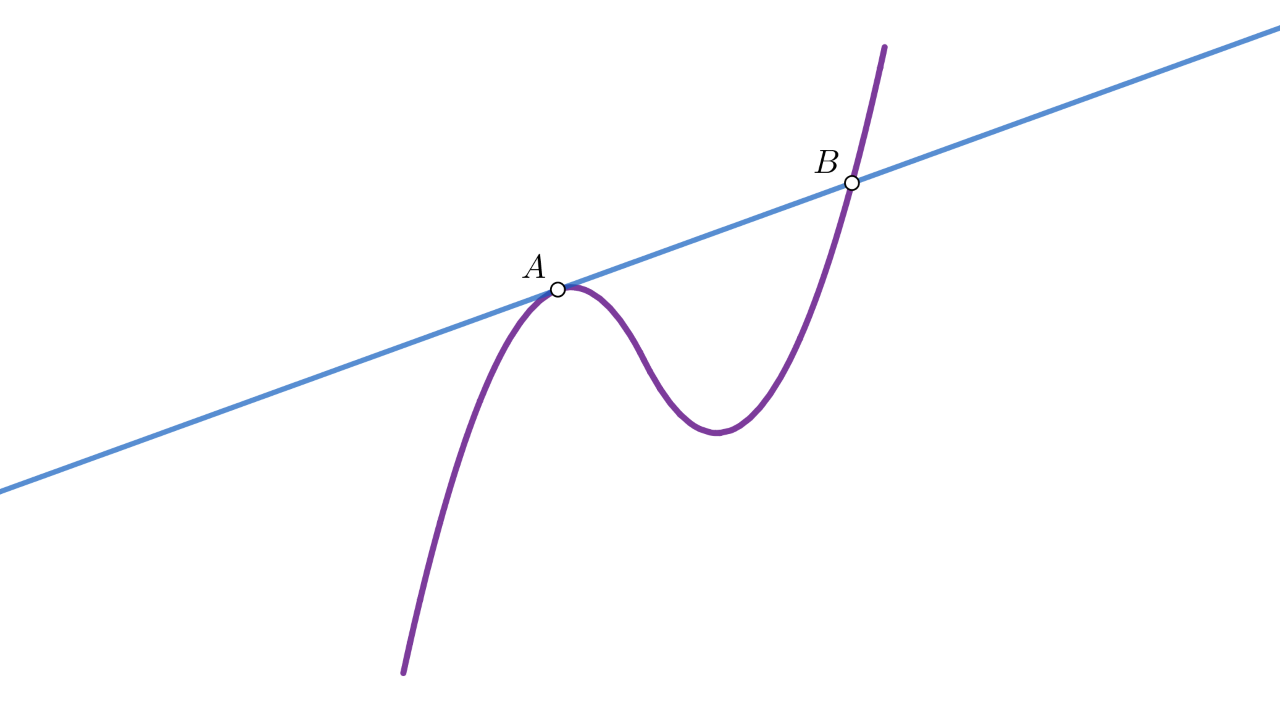
Kako odrediti jednadžbu tangente na neku krivulju? Ponovimo prvo neke pojmove.
Podsjetimo se.
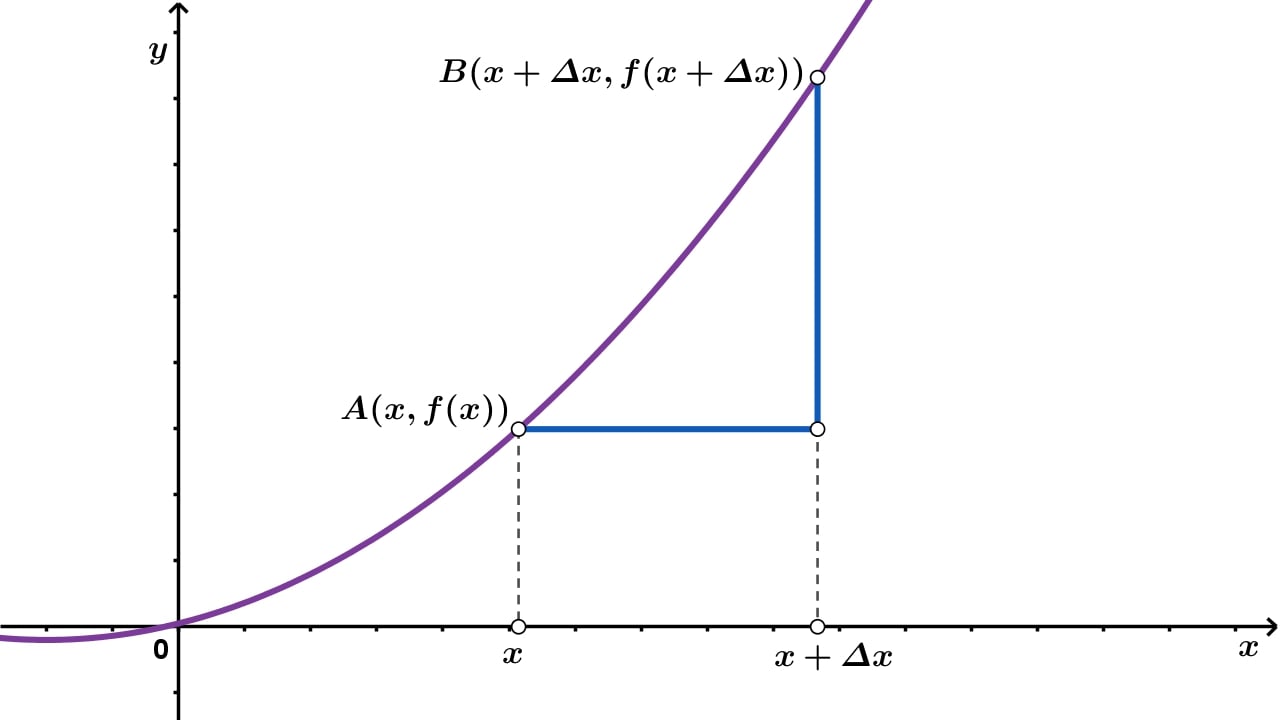
Neka je zadana neka funkcija Označimo početnu vrijednost nezavisne varijable, odnosno argumenta s a novu vrijednost argumenta s Broj
Označite prirast argumenta i prirast funkcije na grafu.
Diferencijalni račun grana je matematike koja je nastala u 17
stoljeću. Sir Isaac Newton (1643. – 1727.) i Gottfried von Leibnitz (1646. – 1716.) zaslužni su za važan iskorak u razmišljanju potrebnom za razvoj diferencijalnog računa. Oba matematičara pokušavala su pronaći algebarsku metodu za računanje koeficijenta smjera tangente u proizvoljnoj točki krivulje i računanje brzine promjene jedne varijable u odnosu na drugu.
|
|
|
|
|
|
|
|
|
|
|
Pravac koji siječe krivulju u dvije točke zove se sekanta. Promotrimo dvije točke i na krivulji. Povucimo sekantu tim dvjema točkama.
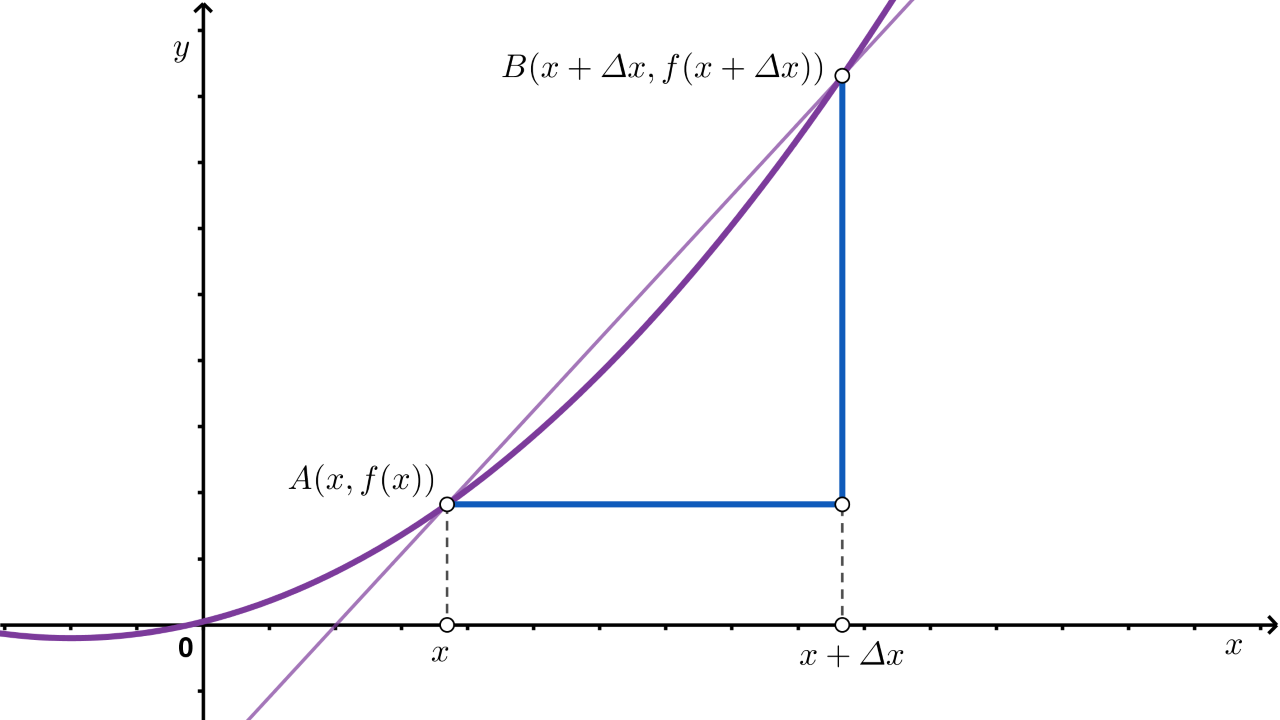
Odredimo koeficijent smjera prikazane sekante.
Istražimo
Proučite sljedeću interakciju. Što se događa kada se točka približava točki
Zato je koeficijent smjera tangente jednak
Primjer 1.
Odredimo koeficijent smjera tangente na graf funkcije u točki
.
Koja je jednadžba te tangente?
Izračunali smo koeficijent smjera
i dana je točka
pa lako izračunamo jednadžbu tangente
Riješite sljedeće zadatke.
Koja je jednadžba tangente na graf funkcije u točki
Što primjećujete? Možete li poopćiti tvrdnju?
Koeficijent smjera tangente je pa je tangenta odnosno taj isti pravac, pa on s grafom ima sve točke zajedničke.
Općenito za linearnu funkciju
vrijedi da je njezina tangenta