


Visina alepskoga bora u metrima može se opisati formulom pri čemu je broj godina nakon što je mladica bora posađena.
Koliko je bila visoka mladica bora?
Kojom brzinom bor raste godinu i pol dana nakon što je mladica posađena, a kojom nakon
godina?
Naučili ste da derivacija funkcije u točki predstavlja brzinu promjene funkcije u toj točki. Budući da je potrebno odrediti brzinu promjene funkcije u i u godina, to znači da treba izračunati i Učinite to!
Što znače dobivene vrijednosti? Koja im je mjerna jedinica?
znači da alepski bor raste brzinom od metra godišnje godinu i pol dana nakon što je posađen, a brzinom od metra godišnje deset godina nakon što je posađen.
Podsjetimo se: derivacija funkcije u nekoj točki predstavlja brzinu promjene te funkcije u toj točki.
Ako funkciju u maloj okolini oko te točke aproksimiramo pravcem, taj će pravac biti
Riješite sljedeće zadatke.
Ako je nekom funkcijom opisana promjena položaja nekoga tijela koje se giba pravocrtno, tada derivacija funkcije predstavlja trenutnu brzinu kojom se to tijelo giba.
Primjer 1.
Automobil vozi po ravnoj cesti. Položaj automobila u odnosu na polaznu točku, izražen u kilometrima, opisuje funkcija pri čemu je vrijeme u satima od početka mjerenja.
- Koji je položaj automobila minuta od početka mjerenja?
- Kolika je brzina automobila u trenutku minuta, minuta?
Što možete zaključiti o gibanju automobila?
Po danoj je funkciji brzina automobila
cijelo vrijeme
, znači možemo zaključiti da se automobil giba jednoliko.
Pogledajmo sada malo drukčiji slučaj.
Primjer 2.
Položaj nekoga tijela na pravcu u centimetrima, u odnosu na zadanu točku opisuje funkcija pri čemu je vrijeme u sekundama,
Pogledajmo animaciju.
Kako se giba tijelo? Tijelo je
Odredimo funkciju koja računa brzinu tijela u bilo kojem trenutku.
Trenutna brzina tijela u trenutku iznosi
Vidimo da je tijelo povećalo brzinu, odnosno ubrzalo je. Koliko iznosi ta promjena brzine?
Iz fizike nam je poznato da je ubrzanje ili akceleracija brzina promjene trenutne brzine nekoga tijela pa možemo zaključiti da je akceleracija derivacija funkcije brzine po vremenu ili druga derivacija funkcije položaja po vremenu.
Odredite funkciju akceleracije!
Zaključujemo da se tijelo giba jednoliko ubrzano.
Primijenite u sljedećim zadatcima.
Znate li kako se računalo prije nego što su postojala računala?
Izvođenje osnovnih računskih radnji relativno je jednostavno, međutim korjenovanje, a naročito računanje vrijednosti eksponencijalnih, logaritamskih i trigonometrijskih funkcija nemoguće je ako želimo dobiti točne rezultate. Zbog toga računamo približno, a teorijska osnova za približno računanje jesu derivacije. Pogledajmo.
Ne koristeći se računalom, izračunajmo približnu vrijednost
U tu svrhu promotrimo funkciju Ona za daje odgovor koji tražimo, Za tu funkciju znamo izračunati bez računala. Primijetimo da dalje računamo a je blizu za koji je poznata vrijednost funkcije
Funkciju
ćemo aproksimirati linearnom funkcijom
koja prolazi točkom
i najbolje se "priljubljuje" grafu funkcije
To je očito tangenta na graf funkcije u točki
Jednadžbu tangente znamo odrediti, njezin koeficijent smjera (vodeći koeficijent
u pravilu pridruživanja funkcije) jednak je derivaciji u zadanoj točki
Provjerite sami da je
Sada ćemo lagano izračunati
Slično možemo nastaviti i dalje, odredit ćemo kvadratnu funkciju koja će najbolje aproksimirati funkciju
Razumno je definirati kvadratnu aproksimaciju funkcije
kao kvadratnu funkciju
za koju je
i
Kolika je sada približna vrijednost
Mogli ste uočiti da je
Očito će aproksimacija biti bolja ako nastavimo i odredimo polinom trećeg, četvrtog,... stupnja.
Općenito vrijedi da funkciju možemo aproksimirati Taylorovim polinomom
U svakome području iz stvarnoga života u kojemu dolazi do promjena pojam derivacije je važan. Pogledajmo jedan zanimljiv primjer iz medicine:
Ateroskleroza je bolest krvožilnog sustava koju karakterizira nakupljanje lipida (masnih stanica) na stijenkama krvnih žila. Pretpostavimo da je presjek aorte krug polumjera i da će debljina naslaga masnih stanica na stijenki aorte, mjerena u centimetrima, nakon godina iznositi Odredite kojom će se brzinom smanjivati protočno područje aorte za godine.
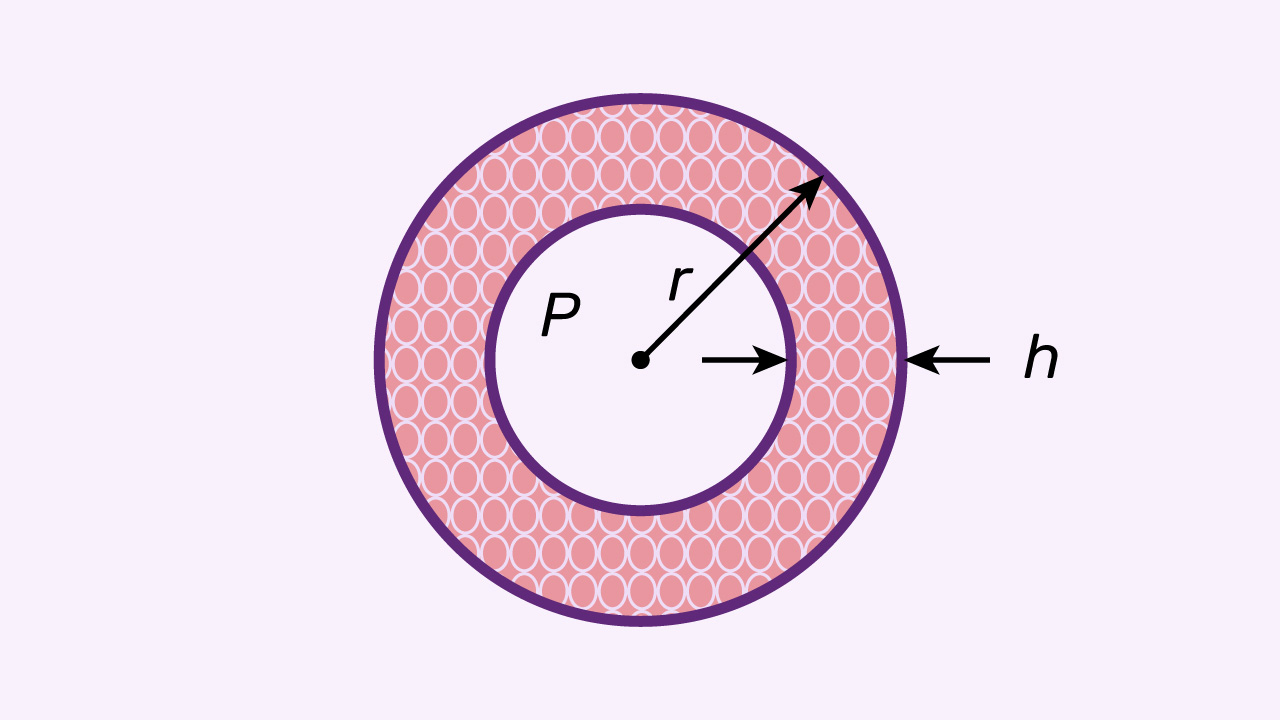
Protočno područje aorte krug je površine Uvrštavanjem danih podataka dobivamo funkciju
Sređivanjem i kvadriranjem izraza slijedi
Funkciju
deriviramo:
Uvrstimo
pa je
odnosno protočno područje aorte za
godine smanjivat će se brzinom od
godišnje.