Postoje li beskonačne sume?

Odgovorit ćemo na pitanja iz uvodnog primjera. Riješite zadatke.

Pogled odozgo na veliku, srednju i malu kocku koje su složene jedna na drugu. — Rješenje uvodnog djela

Pokus

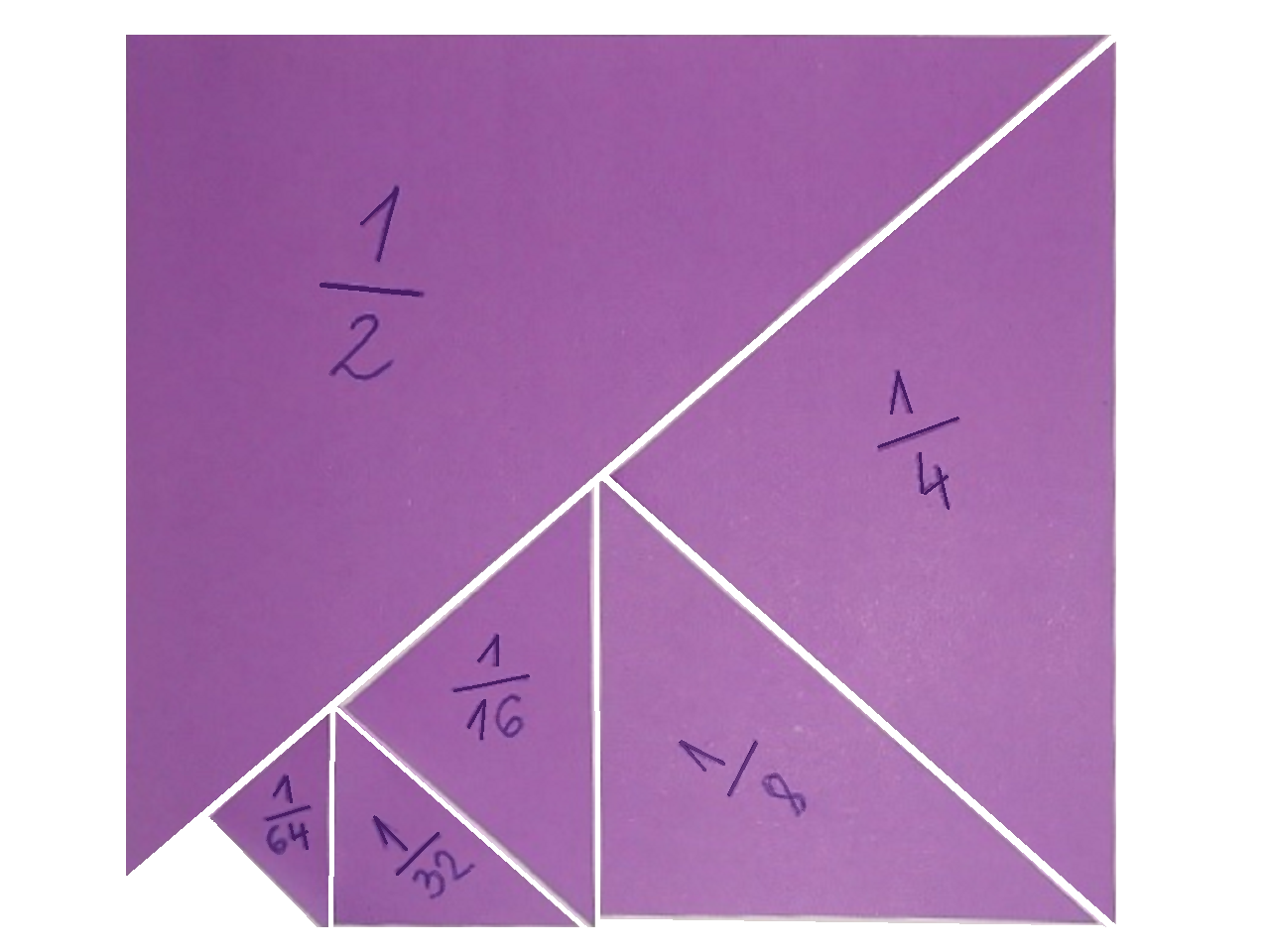
Izrežite kvadrat sa stranicom duljine $1 dm$ od papira. Prerežite ga po dijagonali. Označite na jednom od dobivenih trokuta njegovu površinu u ${dm}^{2} .$ Prerežite drugi trokut tako da dobijete dva sukladna pravokutna trokuta. Na jednom od njih zapišite njegovu površinu, a drugi ponovno prerežite. Ponavljajte ovaj postupak što duže možete. Složite trokute na koje ste zapisali površinu u kvadrat. Jeste li popunili cijeli kvadrat? Zapišite zbroj površina trokuta. Koji ste broj dobili? Kakav biste broj dobili kad bi broj trokuta bio jako velik? Ako zamislimo da ih je beskonačno mnogo, koliki bi bio zbroj svih površina?

Zbroj površina trokuta na slici iznosi: $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} = \frac{63}{64} .$

Ako je broj trokuta iznimno velik, dio koji nedostaje do kvadrata izrazito je mali pa je zbroj površina približno $1 .$ Pokažimo da ćemo do istog zaključka doći i ako računamo zbroj površina trokuta.

Zbrajamo članove geometrijskog niza čiji je prvi član $a_{1} = \frac{1}{2}$ i kvocijent $q = \frac{1}{2} .$ Zbroj prvih $n$ članova je $S_{n} = a_{1} \cdot \frac{q^{n} - 1}{q - 1} = \frac{1}{2} \cdot \frac{{(\frac{1}{2})}^{n} - 1}{\frac{1}{2} - 1} = 1 - {(\frac{1}{2})}^{n} .$ Kad je $n$ jako velik, broj ${(\frac{1}{2})}^{n}$ je blizu $0$ pa je $S_{n} \approx 1 .$

Kad bi trokuta bilo beskonačno mnogo, pokrili bi cijeli kvadrat pa bi zbroj njihovih površina bio $1 .$

Želimo li izračunati tu površinu, treba odrediti limes niza $S_{n} :$

$\lim_{n \to \infty} S_{n} = \lim_{n \to \infty} (1 - {(\frac{1}{2})}^{n}) = 1 - 0 = 1 .$

Kvadrat razrezan na niz sličnih pravokutnih jednakokračnih trokuta. — Geometrijski red

Zadatak 1.

Zamislimo da je u uvodnom primjeru beskonačno mnogo kocaka složeno u toranj.

a. Kolika je ukupna visina tornja?

b. Koliki je ukupni obujam kocaka?

a. Neka je $a_{n}$ duljina stranice $n$ -te kocke. Niz je geometrijski, prvi je član $a_{1} = 1,$ a kvocijent je $q = \frac{1}{2} .$ Zbroj prvih $n$ članova niza iznosi $S_{n} = a_{1} \frac{q^{n} - 1}{q - 1} = \frac{{(\frac{1}{2})}^{n} - 1}{\frac{1}{2} - 1} = 2 (1 - {(\frac{1}{2})}^{n}) .$

Ukupna visina tornja iznosi $\lim_{n \to \infty} S_{n} = \lim_{n \to \infty} 2 (1 - {(\frac{1}{2})}^{n}) = 2 (1 - 0) = 2 .$

b. Neka je $V_{n}$ obujam $n$ -te kocke. Kocke su međusobno slične, $a_{n} : a_{n - 1} = 1 : 2$ pa je $V_{n} : V_{n - 1} = 1 : 2^{3} = 1 : 8 .$ Niz je geometrijski, prvi je član $V_{1} = 1,$ a kvocijent je $q = \frac{1}{8} .$ Zbroj prvih $n$ članova niza iznosi $S_{n} = V_{1} \frac{q^{n} - 1}{q - 1} = \frac{{(\frac{1}{8})}^{n} - 1}{\frac{1}{8} - 1} = \frac{8}{7} (1 - {(\frac{1}{8})}^{n}) .$

Ukupni obujam kocaka iznosi $\lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \frac{8}{7} (1 - {(\frac{1}{8})}^{n}) = \frac{8}{7} (1 - 0) = \frac{8}{7} .$

Primjer 1.

Izračunajmo sumu $2 + \frac{2}{5} + \frac{2}{25} + \frac{2}{125} + . . . + \frac{2}{5^{n}} + . . .$

Pribrojnici čine geometrijski niz jer svaki sljedeći pribrojnik nastaje tako da prethodni množimo s $\frac{1}{5} .$ Prvi je član $a_{1} = 2,$ a kvocijent $q = \frac{1}{5} .$ Zbroj prvih $n$ članova niza iznosi:

$S_{n} = a_{1} \frac{q^{n} - 1}{q - 1} = 2 \cdot \frac{{(\frac{1}{5})}^{n} - 1}{\frac{1}{5} - 1} = \frac{5}{2} (1 - {(\frac{1}{5})}^{n}) .$

Zbroj svih članova niza iznosi:

$\lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \frac{5}{2} (1 - {(\frac{1}{5})}^{n}) = \frac{5}{2} .$

Zadatak 2.

Uparite elemente tako da vrijedi znak jednakosti.

$\frac{3}{4} + \frac{1}{2} + \frac{1}{3} + \frac{2}{9} + \frac{4}{27} + . . . =$	$\frac{4}{9}$
$5 + 1 + \frac{1}{5} + \frac{1}{25} + . . . =$	$\frac{25}{4}$
$3 - 2 + \frac{4}{3} - \frac{8}{9} + \frac{16}{27} - . . . =$	$\frac{9}{4}$
$\frac{2}{3} - \frac{1}{3} + \frac{1}{6} - \frac{1}{12} + . . . =$	$\frac{9}{5}$

null

Ponovimo

U ovoj ste jedinici učili o nizovima. Riješite zadatke vezane uz nizove.

Kolekcija zadataka #2

Razvrstajte nizove $(a_{n})$ s obzirom na njihovu vrstu ako formule vrijede za sve $n \in N .$

$a_{n + 1} = a_{n} + 2 n$

Aritmetički

Geometrijski

Ostalo

null

Niz $(a_{n})$ je aritmetički, a niz $(b_{n})$ geometrijski. Uparite odgovarajuće tvrdnje.

$a_{21} = 55,$ $a_{15} - a_{3} = 36$	$b_{8} = 0.5$
$a_{5} + a_{9} = 40,$ $a_{7} + a_{13} = 58$	$b_{5} = 16$
$b_{2} + b_{5} = 36,$ $b_{2} - b_{5} = 28$	$a_{21} = 62$
$b_{8} + b_{3} = 132,$ $b_{8} \cdot b_{3} = 512,$ rastući niz	$a_{10} = 22$

null

Izračunajte limese i rješenje zapišite kao decimalni broj:

a.

$\lim_{n \to \infty} \frac{3 n - 2}{5 n + 1} =$

b.

$\lim_{n \to \infty} \frac{5 n - 4}{n^{2} + n} =$

.

null

Plaća zaposlenika iznosi $8 000$ kn. Plaće su rasle tri puta po $2 % .$ Nova plaća zaposlenika iznosi

$8 480$ kn

$8 489.66$ kn

$8 640$ kn

null

Neprekidno ukamaćivanje

U jedinici 2.6. računali ste kamate složenim kamatnim računom. Prisjetimo se.

Kolekcija zadataka #3

Iznos od $2 000$ kn uložen je uz kamatnu stopu od $2.5 % .$ Obračun kamata je složen. Odredite iznos nakon $5$ godina ako je

a. pripisivanje kamata godišnje

b. mjesečno

c. dnevno

d. svaki sat.

a.

$C_{5} =$

.

null

b.

$C_{5} =$

.

Pomoć:

Godina ima dvanaest mjeseci pa se u jednoj godini kamata pripisuje dvanaest puta.

null

c.

$C_{5} =$

.

Pomoć:

Godina ima $365$ dana pa će se kamata u jednoj godini pripisati $365$ puta.

null

d.

$C_{5} =$

.

Pomoć:

U jednom danu su $24$ sata pa će u jednoj godini biti $365 \cdot 24 = 8 760$ pripisivanja kamate.

null

U prethodnom se zadatku broj ukamaćivanja povećava pa očekujemo da će iznos nakon pet godina rasti. Mogli bismo očekivati da će iznos biti mnogo veći za veliki broj ukamaćivanja, ali to se nije dogodilo. Vrijednosti su približno $2 266 .$ Pri tome razlike postoje, ali su male.

Primjer 2.

Zamislimo da je iznos od $1$ kn uložen uz stopu od $100 % .$ Popunite u bilježnici tablicu. Rezultate zapišite na pet decimalnih mjesta.

broj ukamaćivanja $k$
iznos $C_{1}$

$1$

$12$

$365$

$1 000$

$10 000$

$100 000$

$1 000 000$

broj ukamaćivanja $k$	iznos $C_{1}$
$1$
$12$
$365$
$1 000$
$10 000$
$100 000$
$1 000 000$

broj ukamaćivanja $k$	iznos $C_{1}$
$1$	$2$
$12$	$2.61304$
$365$	$2.71457$
$1 000$	$2.71692$
$10 000$	$2.71815$
$100 000$	$2.71827$
$1 000 000$	$2.71828$

U prethodnom ste primjeru računali vrijednosti izraza ${(1 + \frac{1}{k})}^{k}$ za različite prirodne brojeve $k .$ Na osnovi rezultata možemo pretpostaviti da se vrijednosti izraza ${(1 + \frac{1}{k})}^{k}$ povećavaju kad se povećava broj $k .$ Također možemo pretpostaviti da ne prelaze neku vrijednost, na primjer, možemo reći da su svi dobiveni brojevi manji od 3. To bi značilo da je niz $a_{k} = {(1 + \frac{1}{k})}^{k}$ rastući i omeđen. Obje se tvrdnje mogu dokazati.

Niz $a_{k} = {(1 + \frac{1}{k})}^{k}$ monoton je i omeđen.

U jedinici 2.5. Limes niza zaključili smo da je konvergentan niz koji je monoton i omeđen, odnosno da omeđen i monoton niz ima limes. Budući da je niz $a_{n} = {(1 + \frac{1}{n})}^{n}$ važan u matematici i primjenama, uvodimo oznaku za njegov limes.

Broj e

Limes niza $a_{n} = {(1 + \frac{1}{n})}^{n}$ nazivamo $e .$

$\lim_{n \to \infty} = {(1 + \frac{1}{n})}^{n} = e$

Primjer 3.

Neka je obračun kamata složen s godišnjom kamatnom stopom $p$ i $k$ godišnji broj pripisivanja kamata. Iznos $C_{n}$ nakon $n$ godina računamo formulom $C_{n} = C_{0} {(1 + \frac{p}{k})}^{n k} .$ Zamislimo da broj pripisivanja $k$ postaje jako velik, odnosno da $k$ teži u beskonačno. Ukamaćivanje pod ovim uvjetima zove se neprekidno ukamaćivanje. Iznos nakon $n$ godina u tom bi slučaju bio $\lim_{k \to \infty} C_{0} {(1 + \frac{p}{k})}^{n k} .$ Uočite niz čiji je limes koji treba izračunati sličan nizu $a_{k} = {(1 + \frac{1}{k})}^{k}$ pa će se u rješenju pojaviti broj $e .$

Iznos $C_{n}$ nakon $n$ godina uz početni iznos $C_{0},$ godišnju kamatnu stopu $p$ i neprekidno ukamaćivanje računamo formulom $C_{n} = C_{0} e^{n p} .$

Zadatak 3.

Iznos od $2 000$ kn uložen je uz kamatnu stopu od $2.5 % .$ Odredite iznos nakon $5$ godina uz neprekidno ukamaćivanje. Usporedite dobiveni iznos s iznosima iz zadatka na početku ovog poglavlja.

$C_{n} = C_{0} e^{n p},$ $C_{5} = 2 000 \cdot e^{5 \cdot 0.025} = 2 000 e^{0.125}$

Računamo džepnim računalom i dobivamo $C_{5} = 2 266.2969 \approx 2 266.30$ kn.

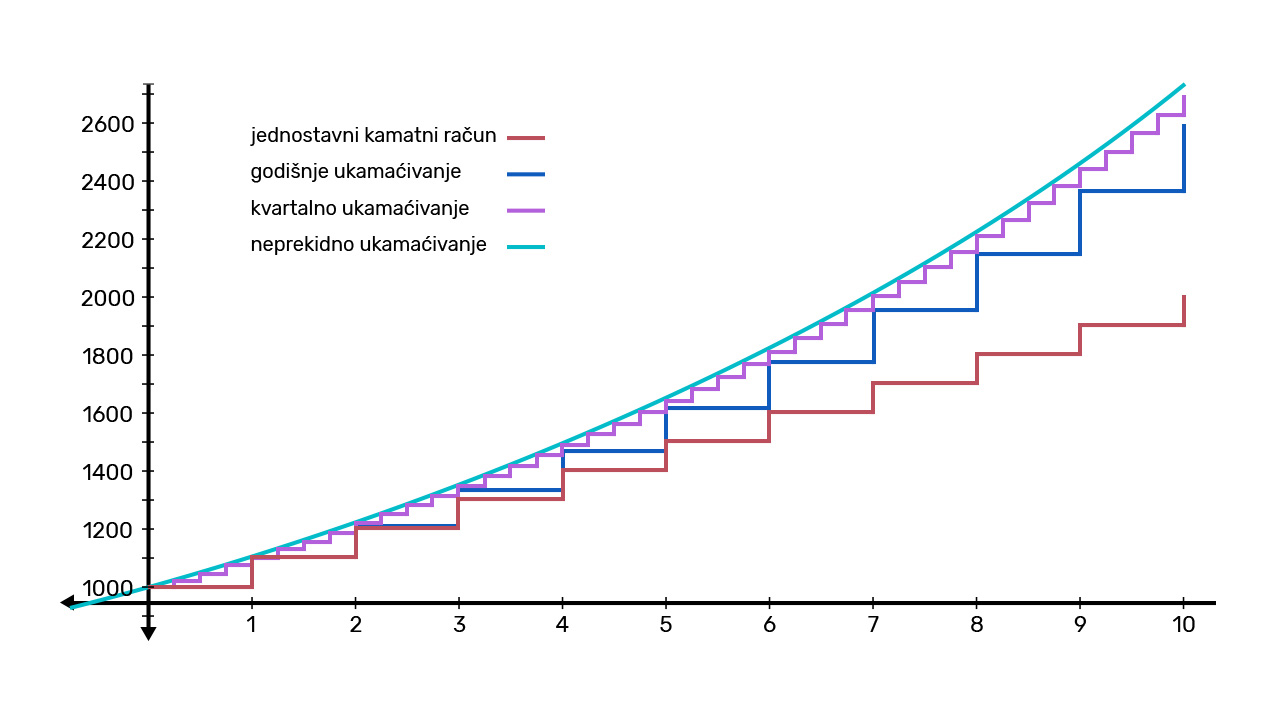
Ako je neki niz rastući i ima limes, svi će članovi niza biti manji od limesa ili jednaki njemu. Primijenimo ovaj zaključak na složeno ukamaćivanje uz $k$ godišnjih pripisivanja kamata i neprekidno ukamaćivanje uz istu početnu vrijednost i kamatnu stopu. Možemo zaključiti da će iznosi uz složeno ukamaćivanje uvijek biti manji od iznosa uz neprekidno ukamaćivanje. Tako nam neprekidno ukamaćivanje može poslužiti pri određivanju najvećeg iznosa koji možemo dobiti uz iste početne vrijednosti i kamatnu stopu bez obzira na broj ukamaćivanja. Ovo možemo uočiti na grafovima na slici. Grafovi koji prikazuju jednostavni i složeni kamatni račun nalaze se ispod grafa koji prikazuje neprekidno ukamaćivanje.

Grafovi prikazuju ovisnost iznosa o godinama za jednostavni kamatni račun, složeni kamatni račun s godišnjim i kvartalnim ukamaćivanjem i neprekidno ukamaćivanje. — Usporedba ukamaćivanja s različitom frekvencijom

Kutak za znatiželjne

Koristeći se $\lim_{n \to \infty} = {(1 + \frac{1}{n})}^{n} = e,$ dokažite da je $\lim_{k \to \infty} C_{0} {(1 + \frac{p}{k})}^{n k} = C_{0} e^{n p} .$ Kojim ste se svojstvima limesa koristili? Istražite vrijede li ta svojstva.

...i na kraju

Višnja i Marko planiraju podići kredit za školarinu u iznosu od $7 000$ eura na rok od $8$ godina. Čuli su da banka nudi takve kredite uz godišnju kamatnu stopu od $4.65 %$ i da se kredit vraća u mjesečnim anuitetima. Zanimalo ih je koliki je iznos anuiteta pa su ga pokušali izračunati.

Višnja je računala ovako:

Posuđujem $7 000$ eura na rok od $8$ godina. Izračunat ću ukupni iznos otplate i podijeliti ga s brojem mjeseci. Dobit ću iznos koji treba plaćati mjesečno:

$C_{8} = 7 000 \cdot {1.0465}^{8} = 10 069.59$ eura, $\frac{10 069.59}{96} = 104.89$ eura. Mjesečno ću plaćati $104.89$ eura.

Marko je računao ovako:

Posuđujem $7 000$ eura na rok od $8$ godina. Podijelit ću iznos koji posuđujem s brojem mjeseci. Tom ću iznosu pribrojiti mjesečne kamate i tako dobiti iznos koji treba plaćati mjesečno.

$\frac{7 000}{96} = 72.92$ eura, $72.92 \cdot {(1 + \frac{0.0465}{12})}^{1} = 73.20 .$

Budući da su dobili različite vrijednosti, potražili su kreditni kalkulator na internetu i upisali podatke. Kalkulator je izračunao da je mjesečni anuitet $87.46$ eura.

Projekt

Istražite kako se računa mjesečni anuitet.

Procijenite svoje znanje

Zbroj svih brojeva djeljivih s tri koji su manji od $1 000$ iznosi

$165 834$

$166 833$

$167 832$

null

Zbroj prvih triju članova geometrijskog niza iznosi

$26,$ a zbroj idućih triju iznosi

$702 .$ Deseti član tog niza je

.

null

Uparite niz i njegov limes.

$\frac{2 n - 5}{4 + n}$
${(\frac{3}{7})}^{n}$
$3 + \frac{4}{3 n}$
$\frac{2 (1 + 2 + . . . + n)}{n^{2}}$

Pomoć:

$1 + 2 + . . . + n$ je zbroj prvih $n$ članova aritmetičkog niza. Primijenite formulu za $S_{n} .$

null

Automobil čija je cijena $98 000$ kn gubi godišnje $16 %$ vrijednosti. Vrijednost automobila, zaokružena na cijeli broj, nakon tri godine iznosi

.

null

Ako se kamate obračunavaju složenim kamatnim računom, iznos oročen uz godišnju kamatnu stopu od

$2 %$ udvostručit će se nakon

godina.

null

2.7 Aktivnosti za samostalno učenje

Na početku...

Postoje li beskonačne sume?

Kolekcija zadataka #1

Pokus

Zadatak 1.

Primjer 1.

Zadatak 2.

Ponovimo

Kolekcija zadataka #2

Aritmetički

Geometrijski

Ostalo

Neprekidno ukamaćivanje

Kolekcija zadataka #3

Primjer 2.

Broj e

Primjer 3.

Zadatak 3.

Kutak za znatiželjne

...i na kraju

Projekt

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: