

Girolamo Cardano, matematičar iz 16. stoljeća, napisao je knjigu Liber de Ludo Aleae (Knjiga o bacanju kocke). U knjizi je zapisao: „Dakle, postoji jedno opće pravilo, naime, trebamo razmatrati cijeli 'krug' (ukupan broj jednako mogućih događaja) i broj bacanja koja predstavljaju broj načina na koje se povoljan rezultat može dogoditi te usporediti taj broj s ostatkom od 'kruga' i na temelju te proporcije potrebno je donijeti uzajamnu okladu tako da se svatko može natjecati pod jednakim uvjetima.“ Jedan od problema koje je riješio je ovaj: Kolika je šansa da se pri bacanju triju kocki dobije zbroj a kolika da se dobije zbroj

Prisjetimo se definicije vjerojatnosti.
Neka je
konačni prostor elementarnih događaja i neka su svi elementarni događaji jednako mogući. Neka je
događaj. Omjer broja elementarnih događaja povoljnih za
i ukupnog broja elementarnih događaja zovemo vjerojatnost događaja
Uočite da su u definiciji dvije bitne pretpostavke o prostoru elementarnih događaja:
Ako je pokus takav da ima beskonačno mnogo elementarnih ishoda, tada vjerojatnost nećemo moći računati po ovoj definciji. Na drugu pretpostavku treba paziti pri opisu elementarnih događaja za neki pokus. Naime, ponekad je moguće na više načina opisati elementarne događaje, a mi ćemo, ako je to moguće, birati onaj pri kojemu su elementarni ishodi jednako mogući.
Primjer 1.
Na slučajan način biramo jednu znamenku. Kolika je vjerojatnost da je djeljiva s tri?
Odredimo najprije prostor elementarnih događaja i broj elemenata skupa
Elementarnih je ishoda konačno mnogo. Svi su jednako mogući jer u zadatku piše da se znamenke biraju na slučajan način.
Događaj čija se vjerojatnost traži, je pa je
Vjerojatnost događaja je
Na slučajan način biramo dvije različite znamenke. Kolika je vjerojatnost da su obje djeljive s tri?
Redoslijed biranja znamenki nije bitan, a važno je da su znamenke različite. Prostor elementarnih događaja je skup
Odredimo broj elemenata skupa
Na koliko načina možemo iz skupa od
elemenata odabrati
Prisjetite se kombinacija i binomnih koeficijenata:
označava broj načina na koji možemo iz skupa od
elemenata odabrati
elemenata.
Stoga je
Odredimo događaj
Obje odabrane znamenke trebaju biti djeljive s tri. To znači da iz skupa
biramo dva pa je
Vjerojatnost događaja
je
Na slučajan način biramo šifru koja se sastoji od dviju znamenki. Kolika je vjerojatnost da su obje znamenke djeljive s tri?
U ovom je zadatku redoslijed znamenaka bitan jer se, naprimjer, šifre i razlikuju. Znamenke se mogu ponavljati, a prva od njih može biti
Odredimo broj elemenata skupa Na koliko načina možemo izabrati dvije znamenke uzimajući u obzir redoslijed? Prisjetite se varijacija. Prvu znamenku možemo odabrati na načina, drugu također na Stoga je
Odredimo događaj Obje odabrane znamenke trebaju biti djeljive s tri. To znači da prvu možemo odabrati na načina, drugu također na pa je Vjerojatnost događaja je
Odredite vjerojatnosti u zadatcima s kockama.
Riješimo uvodni zadatak. Kolika je vjerojatnost da se pri bacanju triju kocki dobije zbroj a kolika da se dobije zbroj Riješite zadatak, a rješenje provjerite u videozapisu.
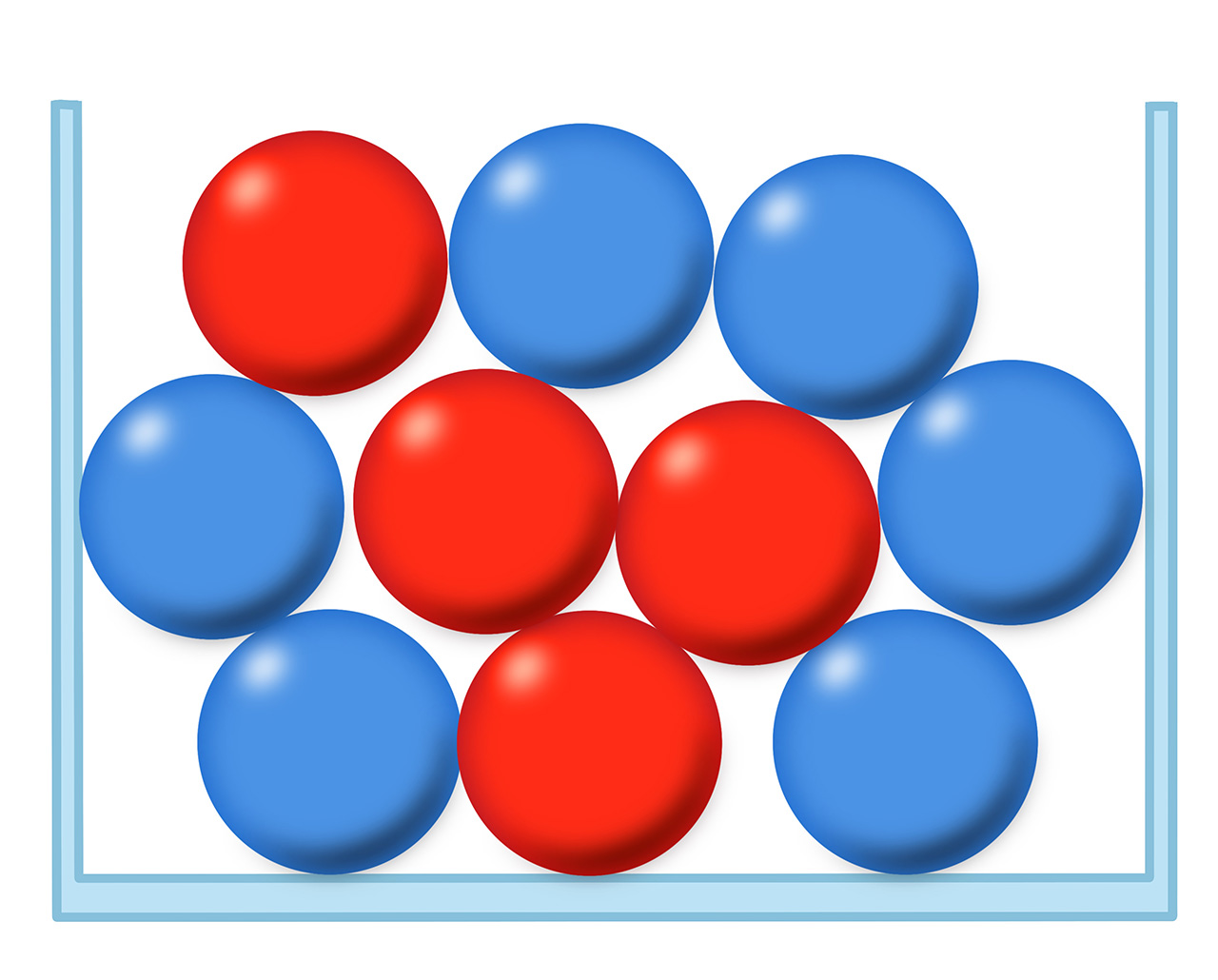
U posudi se nalaze četiri crvene i šest plavih kuglica. Nasumice izvlačimo jednu. Kolika je vjerojatnost da je izvučena plava kuglica.
U posudi se nalaze četiri crvene i šest plavih kuglica. Nasumice izvlačimo dvije odjednom. Kolika je vjerojatnost da su obje kuglice plave?
U posudi se nalaze četiri crvene i šest plavih kuglica. Nasumice izvlačimo tri. Kolika je vjerojatnost da su izvučene dvije plave kuglice i jedna crvena?
Kako računamo vjerojatnost unije dvaju događaja? Odgovorite na pitanja.
Zaključimo prethodna razmatranja.
Vjerojatnost unije
Za proizvoljne skupove i vjerojatnost unije računamo kao
Ako je onda vrijedi
Primjer 2.
Jednom bacamo kocku. Kolika je vjerojatnost da je pao neparan broj ili broj djeljiv s tri? Označimo događaje koji se pojavljuju u pitanju:
Treba odrediti S obzirom na to da postoji broj koji je neparan i djeljiv s događaji i imaju neprazni presjek pa vjerojatnost unije računamo formulom
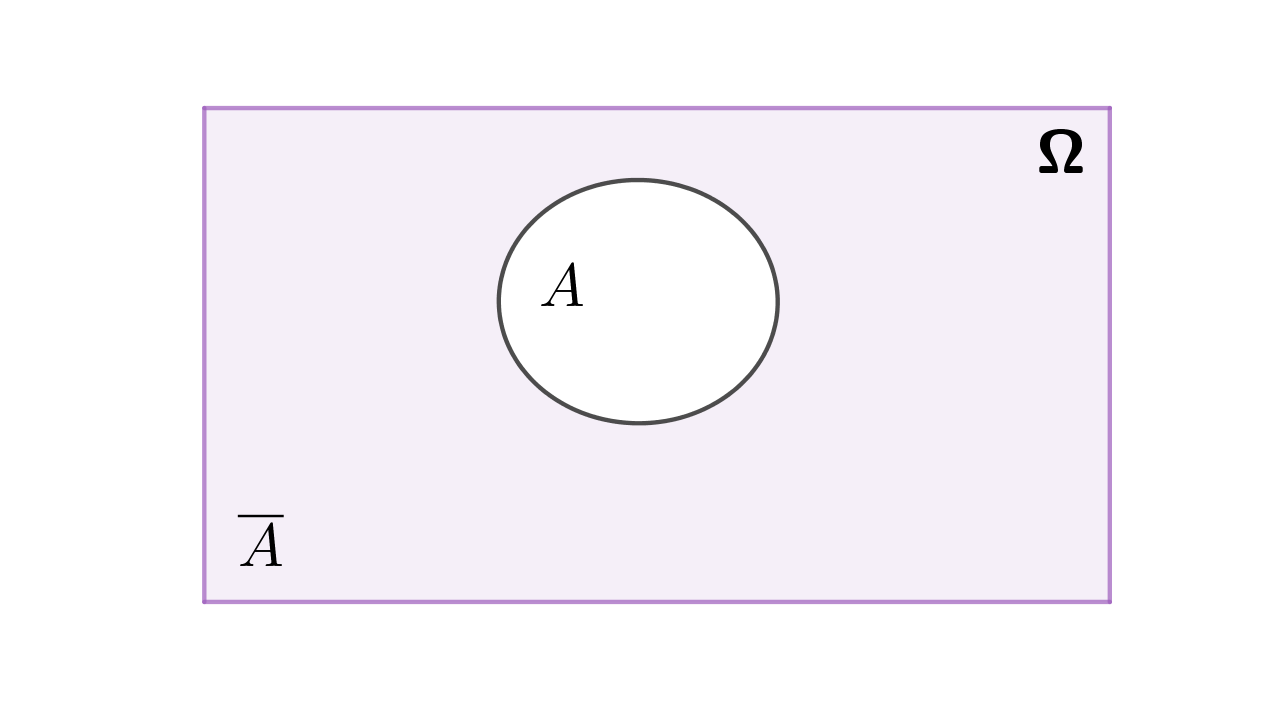
Kako su povezani događaj i njegov komplement, a kako njihove vjerojatnosti?
Poredajte korake izvoda.
Pomoć:
Zapišimo dobivenu formulu.
Vjerojatnost komplementa
Vjerojatnost komplementa računamo kao
U izvodu smo izračunali vjerojatnost
Odaberite u interakciji pokus s kockama ili kuglicama. Odaberite broj kockica ili broj kuglica plave i crvene boje. Izračunajte vjerojatnost zadanog događaja, upišite dobiveni broj pa provjerite rješenje. Odabirom novog zadatka pojavit će se novi događaj.