

U testu iz Geografije je
pitanja na koje Tin može odgovoriti samo s da ili ne. Kako zbog bolesti dugo nije bio na nastavi i ne zna ništa od sadržaja koje se ispituje, pitao se je li pogađanje odgovora dobra strategija.
Pokus
Tin je odlučio upotrijebiti simulaciju bacanja novčića. Na pitanje iz testa će odgovoriti s Ne ako pri bacanju novčića padne glava, a odgovorit će s Da ako padne pismo. Može upotrijebiti interakciju u kojoj se za svako pitanje baca kovanica od 2 kune. U prvom redu tablice je niz točnih odgovora za test iz geografije. Odgovor Da je pogođen ako je na novčiću palo pismo ("broj 2"), a odgovor Ne je pogođen ako je na novčiću pala glava ("riba"). Za pogođeni odgovor u tablici se bilježi znak a ako odgovor nije pogođen znak Broj pogođenih odgovora se bilježi u zadnjem stupcu.
Što će Tin odlučiti ako je za prolaznu ocjenu potrebno najmanje sedam točnih odgovora?
Izračunajte vjerojatnost da Tin
a. dobije prolaznu ocjenu na testu
b. dobije prolaznu ocjenu na testu ako na prva dva pitanja zna točan odgovor.
a. Računamo vjerojatnost događaja koji se ponavljaju, odnosno da se uspjeh desi bar sedam puta:
b. Ako Tin zna odgovore na prva dva pitanja, računamo vjerojatnost da točno odgovori na bar pet pitanja od preostalih osam:
U sljedećim zadatcima ponovit ćete različite prikaze prostora elementarnih događaja i računanje vjerojatnosti korištenjem tih prikaza.
U trgovini odjećom veste se prodaju u bijeloj (B) i plavoj (P) boji te u četiri različite veličine (S, M, L, XL). Ustanovljeno je da kupci biraju boje u omjeru
a veličine ovisno o boji.
Bijele biraju u omjeru
a plave u omjeru
Prikažite prostor elementarnih događaja upotrebljavajući vjerojatnosno stablo.
Upotrebljavajući vjerojatnosno stablo riješite zadatke koji slijede.

Ana na slučajan način slaže četiri knjige, A, B, C i D na policu. Odredite prostor elementarnih događaja, odnosno ispišite listu svih elementarnih događaja i izračunajte vjerojatnost događaja:
a.
b.
c.
a.
b.
c.
Za događaje i vrijedi da je i
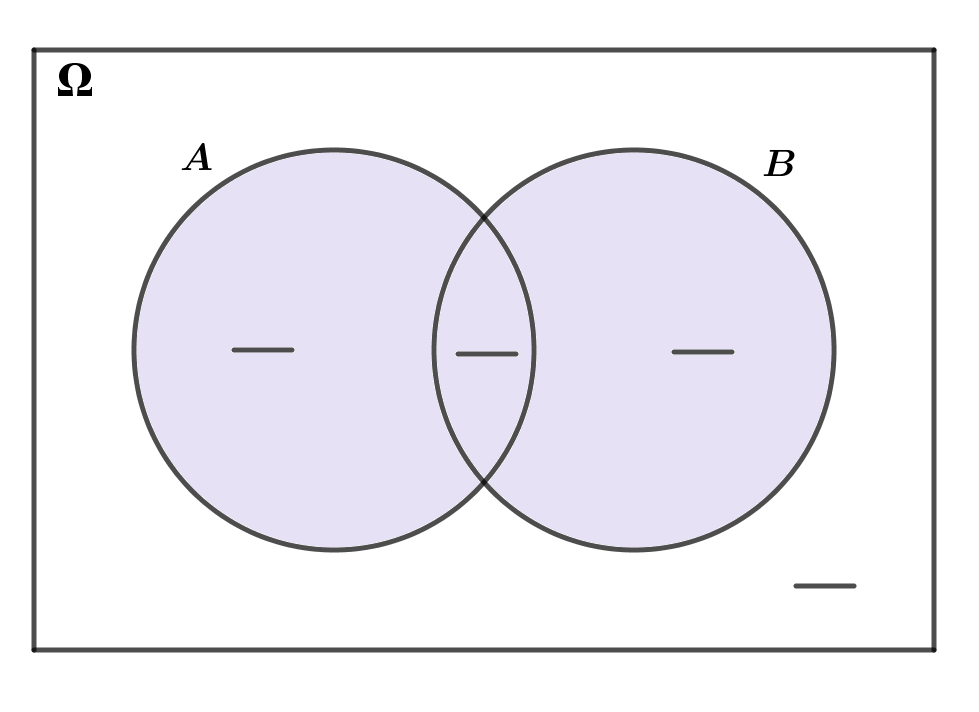
Na sljedećoj slici je Vennov dijagram. Dopunite, povlačenjem na označena mjesta, tako da on prikazuje događaje
i
a zatim riješite zadatke koji slijede.
Postupak:
Odredite sljedeće vjerojatnosti (u decimalnom zapisu):
Istražimo
Za dijagnosticiranje bolesti X otkriven je novi test. Kako bi se provjerila njegova pouzdanost, provedeno je testiranje na pacijenata za koje se zna da njih ima bolest X, a njih nema. Rezultati testiranja dani su sljedećom tablicom.
| Pozitivan rezultat testa |
Negativan rezultat testa |
|
|---|---|---|
| Ima bolest X | ||
| Nema bolest X |
Test je pouzdan ako s velikom vjerojatnošću daje pozitivan rezultat kod pacijenata koji imaju bolest X, a negativan kod onih koji je nemaju. Liječnik će se koristiti testom ako je njegova pouzdanost veća od
Istražite pouzdanost testa za bolest X.
Koristeći se tablicom, odgovorite na sljedeća pitanja.

Imaju li u tvom razredu barem dvije osobe rođendan istog dana? Izračunajte vjerojatnost da barem dvije osobe u grupi od pet imaju rođendan istoga dana? Istražite kako vjerojatnost da barem dvije osobe u grupi imaju rođendan istoga dana ovisi o broju osoba
u grupi. Koji je najmanji broj osoba u grupi za koju je ta vjerojatnost veća od
Jeste li očekivali takav rezultat?
Ako niste riješili zadatak, pogledajte rješenje u sljedećem videozapisu.
Primjer 1.
Tena i Ante odlučili su odigrati sljedeću igru. Stavili su u kutiju četiri bijela i dva crna žetona. Svatko od njih na slučajan način uzima jedan žeton (bez vraćanja). Tena pobjeđuje ako su oba žetona iste boje, a Ante ako su različite boje. Je li igra pravedna? Ako nije, tko ima veće šanse za pobjedu?
Kažemo da je igra pravedna ako svi imaju jednaku šansu za pobjedu, odnosno vjerojatnost pobjede svakog igrača je jednaka.
Izračunajmo vjerojatnost da je pobjedila Tena odnosno da je pobjedio Ante.
Prikazat ćemo ishode koristeći se vjerojatnosnim stablom.
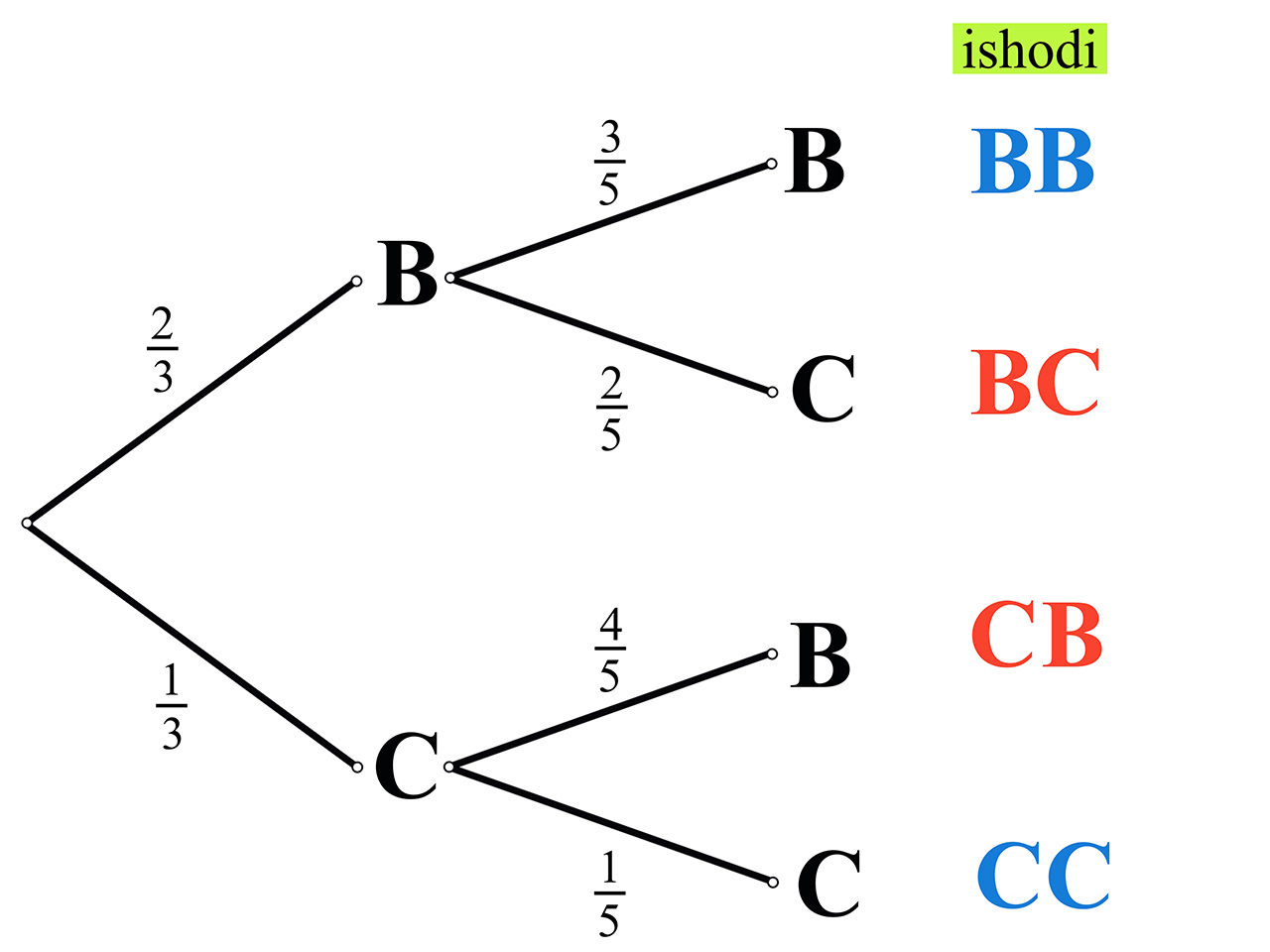
Koristeći se vjerojatnosnim stablom uparite sljedeće vjerojatnosti.
|
|
|
|
|
Veće šanse za pobjedu ima
Postupak:
Kako je vjerojatnost da izvučemo žetone različite boje veća od vjerojatnosti da izvučemo žetone iste boje, igra nije pravedna. Ante ima veće šanse za pobjedu.
Istražimo
Kako bismo popravili igru tako da ona bude pravedna?
Koliko žetona od svake boje treba staviti u kutiju kako bi igra bila pravedna? Pokušajte pronaći bar jedan primjer.
Na primjer, igra je pravedna ako u kutiju stavimo:
crna i
bijeli žeton,
crnih i
bijela žetona,
crnih i
bijelih žetona...
Svaka od nabrojenih mogućnosti vrijedi i ako zamijenimo boje.
Odredite općenito uvjet na broj crnih žetona i broj bijelih žetona tako da igra koju igraju Tena i Ante bude pravedna.
Jedna od igara u zabavnom parku je kolo sreće s osam jednakih dijelova označenih brojevima od do Igrač dobiva žetone koje može iskoristiti za bilo koju igru u zabavnom parku. Broj žetona koji će igrač dobiti ovisi o broju na kojem se zaustavi kolo sreće, kao što je dano u tablici.
| Broj | ||||||||
| Dobitak |
Kako bi igrač jednom zavrtio kolo sreće mora dati pet žetona.
Je li igra pravedna?
Ako nije, kako biste organizirali igru da bude pravedna, a kako da igrač pobjeđuje s vjerojatnošću od
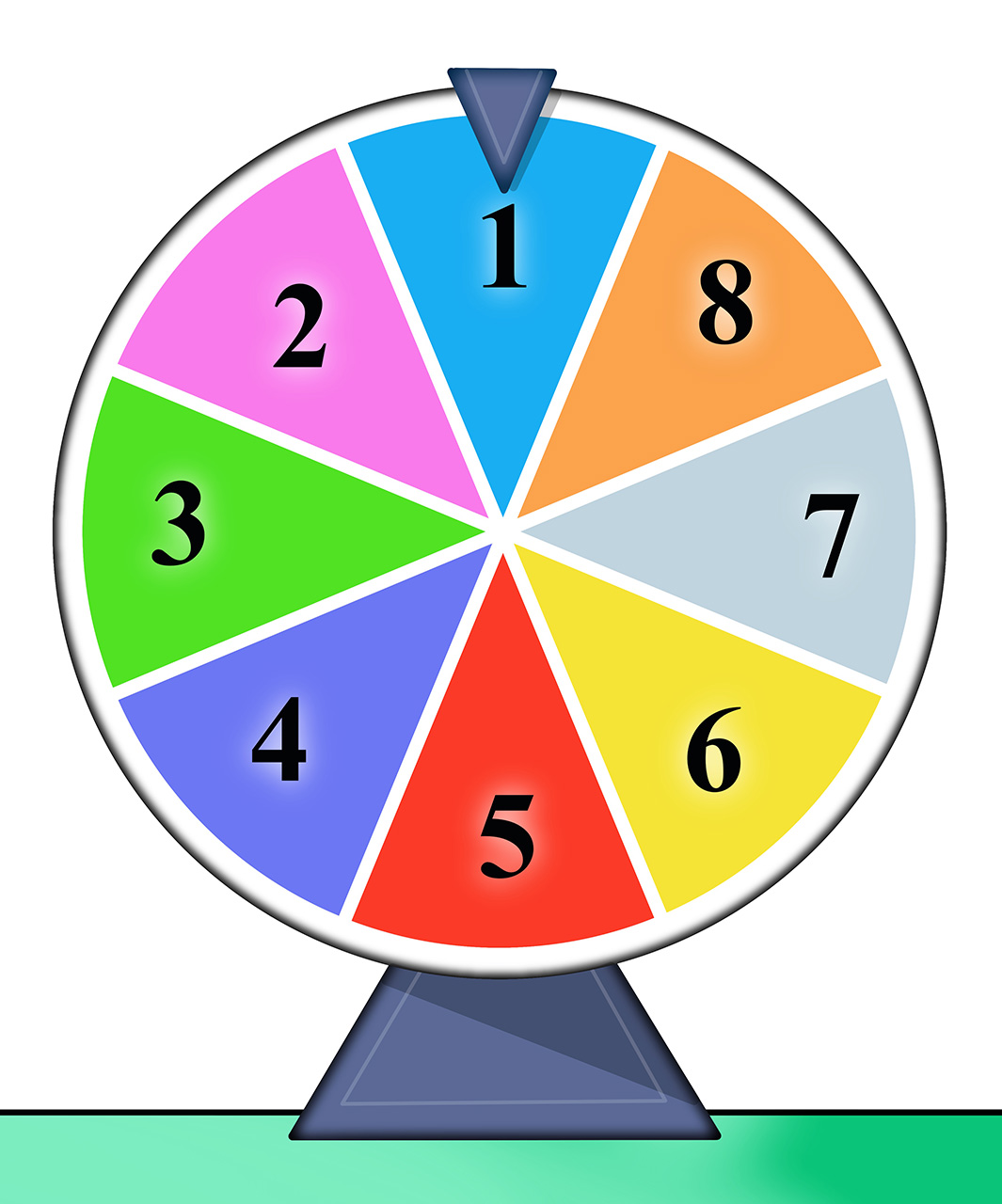
Vjerojatnost da se okrene jedan od osam brojeva je pa u jednoj vrtnji očekujemo dobitak od
žetona.
Ako moramo uložiti pet žetona, očekivano je da ćemo biti na gubitku jedan žeton, što znači da igra nije pravedna.
Kako biste igru učinili pravednom, povećajte broj žetona na nekim poljima, primjerice na svakom polju povećajte za jedan žeton.