

Vjerojatnost da će padati kiša je Ako pada kiša, vjerojatnost da će Marko igrati nogomet je Ako ne pada kiša, vjerojatnost da će Marko igrati nogomet je
Neka je događaj
i događaj
Nacrtajte vjerojatnosno stablo za događaje i
Jesu li događaji
i
nezavisni?
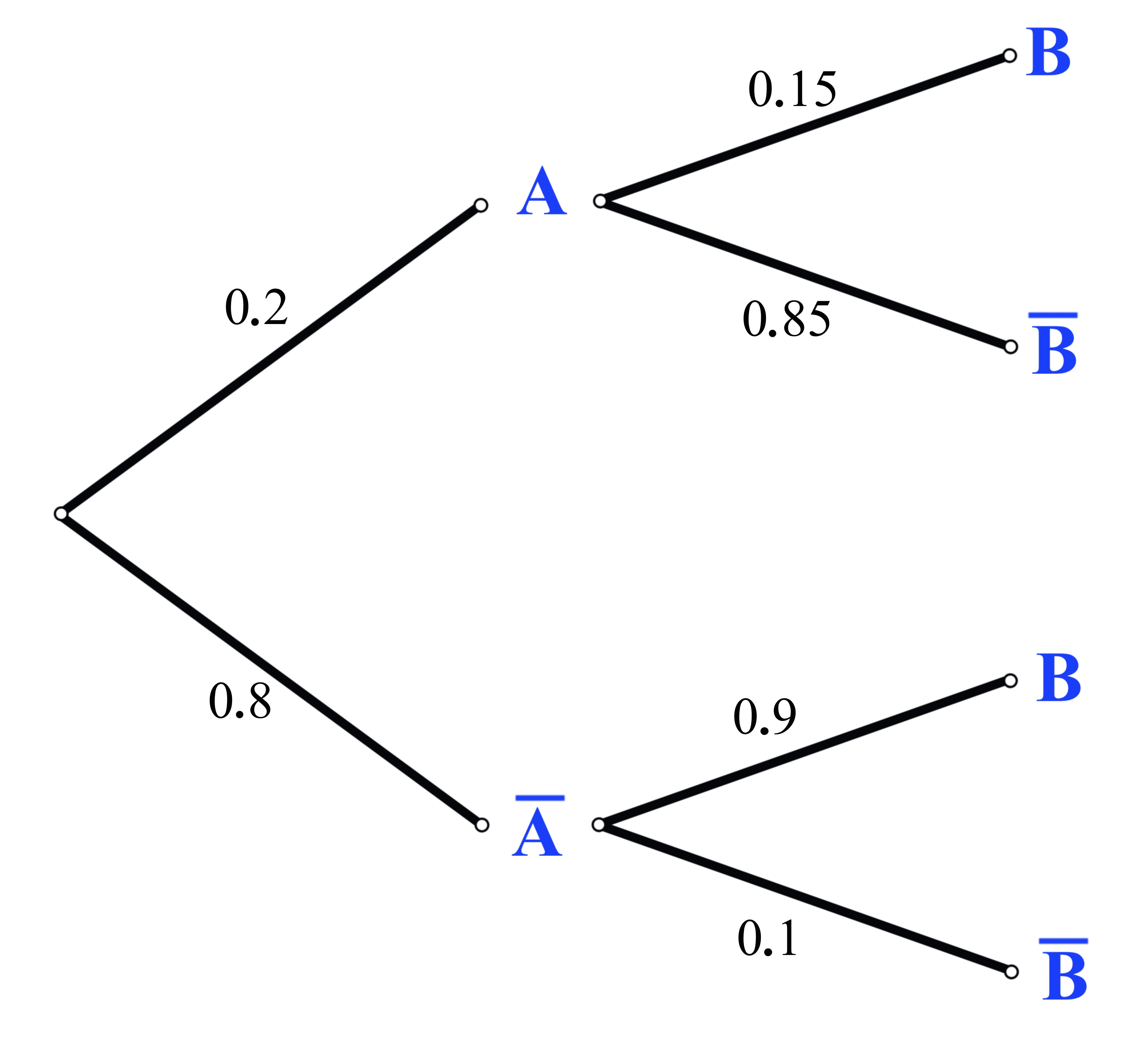
Kolika je vjerojatnost da Marko ne igra nogomet ako pada kiša?

Očito događaji i nisu nezavisni, vjerojatnost da Marko igra nogomet ovisi o tome pada li kiša ili ne.
Vjerojatnost da Marko ne igra nogomet ako pada kiša je
Vjerojatnost događaja uz uvjet da se dogodio događaj označavamo i zovemo uvjetna vjerojatnost.
Označimo uvjetne vjerojatnosti na vjerojatnosnome stablu.
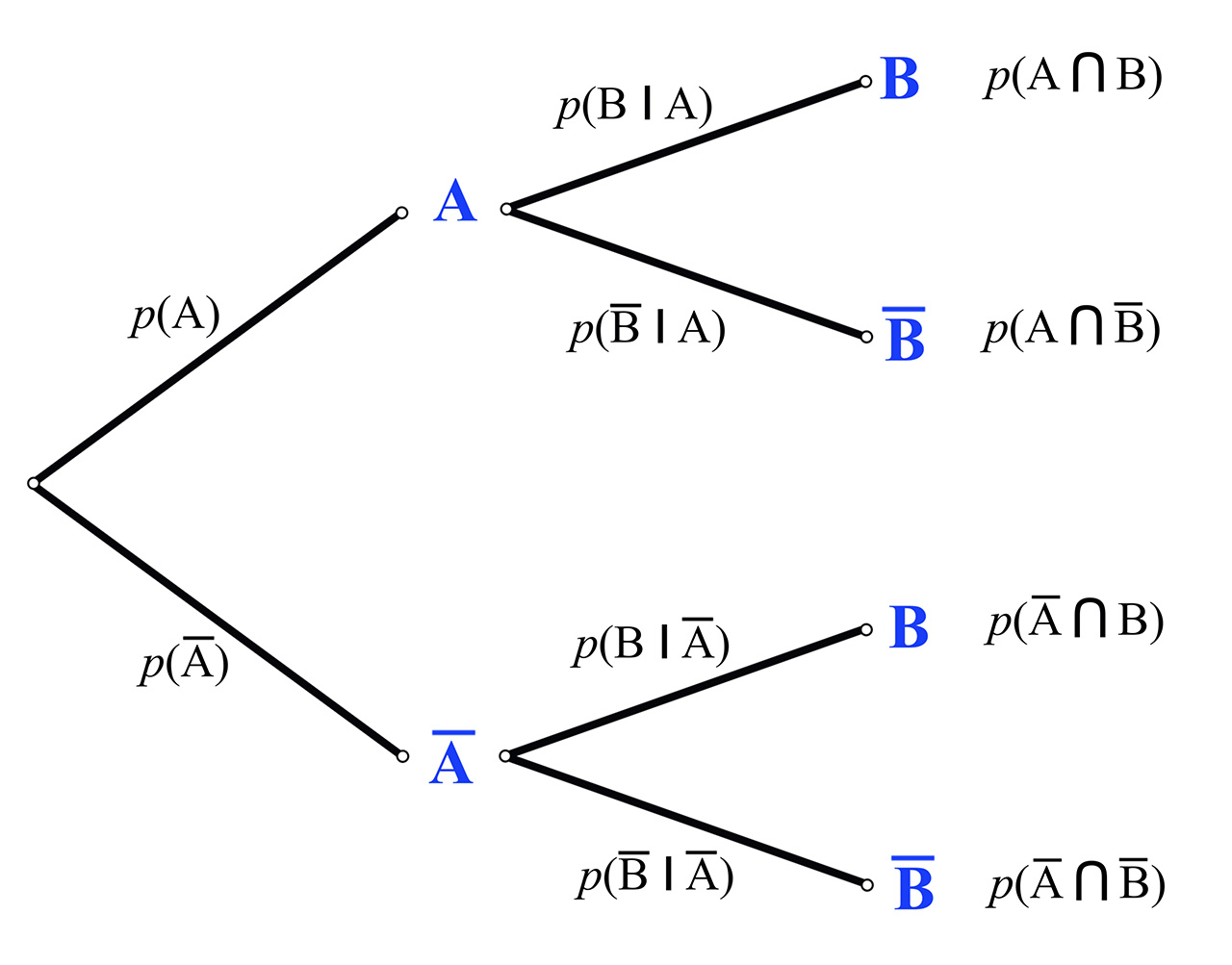
Množimo li duž grane vjerojatnosti za događaj i događaj dobivamo
odnosno
Neka su
i
proizvoljni događaji takvi da je
Uvjetna vjerojatnost događaja
uz uvjet da se ostvario događaj
jest
Pogledajmo još jedan primjer.
Primjer 1.
U posudi je zelenih i plavih kuglica. Na slučajan način izvlačimo dvije kuglice, jednu po jednu. Nacrtajmo vjerojatnosno stablo. Kolika je vjerojatnost da je druga izvučena kuglica plava ako je prva isto bila plava?
Moramo razlikovati dva slučaja.
1. Ako prvu kuglicu nakon izvlačenja vraćamo u posudu, onda su to dva nezavisna događaja.
2. Ako prvu kuglicu nakon izvlačenja ne vraćamo u posudu, onda u drugom izvlačenju imamo ukupno jednu kuglicu manje. Ako smo u prvom izvlačenju izvukli jednu plavu kuglicu, za drugo je izvlačenje preostalo plavih kuglica.
U sljedećem ćemo primjeru primijeniti formulu.
Primjer 2.
U jednom je razredu od ukupno učenika njih dobilo odličan na maturi iz Matematike, a je dobilo odličan iz Matematike i Hrvatskog jezika. Kolika je vjerojatnost da je slučajno odabrani učenik toga razreda dobio odličan iz Hrvatskog jezika ako je poznato da je dobio odličan iz Matematike?
Označimo događaje:
i
Sada je po formuli za uvjetnu vjerojatnost:
Za računanje uvjetne vjerojatnosti možemo se koristiti Vennovim dijagramima.
Primjer 3.
Sonja je istraživala postoji li veza između visine učenika i njihove ljubavi prema košarci. Anketirala je učenika, učenika su viša od učenika voli košarku, a je učenika niže od i ne vole košarku.
Nacrtajmo Vennov dijagram.
Kolika je vjerojatnost da nasumice izabrani učenik voli košarku ako se zna da je viši od
Označimo događaje
i
Neka je broj učenika koji su viši od i voli košarku.
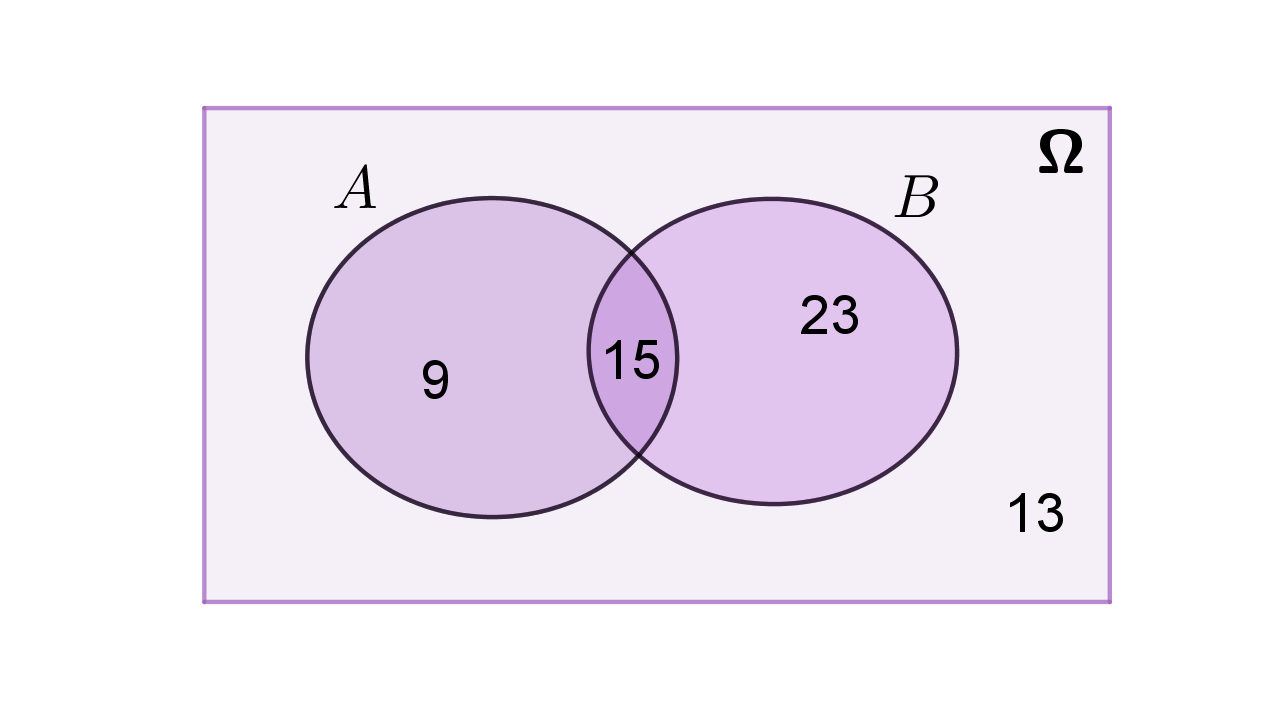
Nacrtajmo Vennov dijagram.
Vjerojatnost da učenik voli košarku ako se zna da je viši od
iznosi
Bacamo kocku. Kolika je vjerojatnost da je pao paran broj ako znamo da je pao broj manji od
U sljedećim zadatcima s bacanjem dvije kocke upotrebljavate dani prikaz prostora elementarnih događaja.

Monty Hall problem je poznat i kao problem s troja vrata:
U igranoj emisiji Let's Make a Deal nalaze se troja vrata. Iza jednih je vrata automobil, dok su iza preostalih dvoja vrata koze. Nakon što odaberete jedna vrata, otvaraju se jedna od preostalih vrata iza kojih je koza. Sada vam se daje mogućnost da se držite svog prvobitnog odabira ili se predomislite i odaberete druga vrata.
Što je vjerojatnije?
(a) Osvojiti automobil ako se držite prvobitnog odabira vrata?
(b) Osvojiti automobil ako promijenite svoje mišljenje i odaberete druga vrata?
Pogledajmo rješenje.