Matematika 4 - 3.3 Parnost i neparnost funkcije

Potencije

Promotrimo funkcije zadane pravilom pridruživanja $f (x) = x^{n},$ $f (x) = x^{n},$ $n \in N$ $n \in N$ i neka njihova svojstva.

Istražimo

U bilježnici popunite tablicu:

$x$ $x$ $- 3$ $- 3$ $- 2$ $- 2$ $- 1$ $- 1$ $1$ $1$ $2$ $2$ $3$ $3$

$f (x)$ $f (x)$ $=$ $=$ $x^{2}$ $x^{2}$

$g (x)$ $g (x)$ $=$ $=$ $x^{4}$ $x^{4}$

Promotrite predznake brojeva u tablici. Zapišite što vrijedi za brojeve i funkcije u tablici. Pronađite još neke brojeve za koje vrijedi isto svojstvo pa ga zapišite. Vrijedi li svojstvo za svaki broj $x ?$ $x ?$ Koristeći se zaključcima, označite točne odgovore za funkcije $f$ $f$ i $g .$ $g .$

Kolekcija zadataka #1

Uparite jednake vrijednosti.

$g (- 3) =$ $g (- 3) =$	$g (3)$ $g (3)$
$f (- 3) =$ $f (- 3) =$	$f (1)$ $f (1)$
$f (- 2) =$ $f (- 2) =$	$f (2)$ $f (2)$
$f (- 1) =$ $f (- 1) =$	$f (3)$ $f (3)$
$g (- 2) =$ $g (- 2) =$	$g (2)$ $g (2)$

null

Za svaki realni broj $x$ $x$ vrijedi: $f (- x)$ $f (- x)$

f (x),

$f (x),$

g (- x)

$g (- x)$

g (x) .

$g (x) .$

null

Označite funkcije za koje vrijedi: $f (- x) = f (x)$ $f (- x) = f (x)$ za svaki realni broj $x .$ $x .$

f (x) = x

$f (x) = x$

f (x) = x^{2}

$f (x) = x^{2}$

f (x) = x^{3}

$f (x) = x^{3}$

f (x) = x^{4}

$f (x) = x^{4}$

f (x) = x^{5}

$f (x) = x^{5}$

f (x) = x^{6}

$f (x) = x^{6}$

f (x) = x^{7}

$f (x) = x^{7}$

f (x) = x^{8}

$f (x) = x^{8}$

null

Zadana je funkcija $f (x) = x^{n} .$ $f (x) = x^{n} .$ Ako za svaki realni broj $x$ $x$ vrijedi $f (- x) = f (x),$ $f (- x) = f (x),$ onda je eksponent $n$ $n$

paran

neparan.

null

Parne funkcije

U prethodnim smo zadatcima promatrali funkcije $f (x) = x^{n} .$ $f (x) = x^{n} .$ Vidjeli smo da za parne ekponente $n$ $n$ vrijedi: za svaki realni broj $x$ $x$ je $f (- x) = f (x) .$ $f (- x) = f (x) .$ Zato ćemo za sve funkcije koje imaju to svojstvo reći da su parne.

Parne funkcije

Za funkciju $f$ $f$ kažemo da je parna ako je za svaki $x$ $x$ iz domene funkcije $f$ $f$ i $- x$ $- x$ u domeni i vrijedi $f (- x) = f (x) .$ $f (- x) = f (x) .$

Zadatak 1.

Promotrite elementarne funkcije: $f (x) = | x |,$ $f (x) = |x|,$ $g (x) = \sqrt{x},$ $g (x) = \sqrt{x},$ $h (x) = \frac{1}{x},$ $h (x) = \frac{1}{x},$ $i (x) = a^{x},$ $i (x) = a^{x},$ $j (x) = {log}_{a} x,$ $j (x) = \log_{a} x,$ $k (x) = sin x,$ $k (x) = \sin x,$ $l (x) = cos x,$ $l (x) = \cos x,$ $m (x) = tg x .$ $m (x) = tg x .$ Koje su od njih parne?

Parne su $f (x) = | x |$ $f (x) = |x|$ i $l (x) = cos x$ $l (x) = \cos x$ .

Primjer 1.

Provjerimo je li funkcija zadana s $f (x) = x^{2} + cos x$ $f (x) = x^{2} + \cos x$ parna. Funkcija je definirana za svaki realni broj $x .$ $x .$ Računamo:

$f (- x) = {(- x)}^{2} + cos (- x) = x^{2} + cos x = f (x) .$ $f (- x) = {(- x)}^{2} + \cos (- x) = x^{2} + \cos x = f (x) .$

Funkcija je parna.

Je li funkcija zadana s $f (x) = \frac{2 x^{2}}{1 + x^{4}}$ $f (x) = \frac{2 x^{2}}{1 + x^{4}}$ parna?

Da

Ne

null

Je li funkcija zadana s $f (x) = \frac{x^{2} + x^{3}}{1 + x^{4}}$ $f (x) = \frac{x^{2} + x^{3}}{1 + x^{4}}$ parna?

Da

Ne

null

Graf parne funkcije

Istražimo

Promotrite grafove parnih funkcija. Uočavate li neko zajedničko svojstvo?

Graf kvadratne funkcije 1/3

Graf funkcije apsolutne vrijednosti 2/3

Graf funkcije kosinus 3/3

Vrijedi li isto svojstvo za sve parne funkcije? Pogledajte u animaciji.

Zaključujemo da se na grafu parne funkcije nalaze točke $(- x, y)$ $(- x, y)$ i $(x, y)$ $(x, y)$ za svaki broj $x$ $x$ iz domene funkcije.

Graf parne funkcije simetričan je s obzirom na os ordinata.

Kolekcija zadataka #2

Je li funkcija čiji je graf na slici parna?

Da

Ne

null

Je li funkcija čiji je graf na slici parna?

Da

Ne

null

Je li funkcija čiji je graf na slici parna?

Da

Ne

null

Je li funkcija čiji je graf na slici parna?

Da

Ne

null

Neparne funkcije

Istražimo

Promatrali smo funkcije zadane pravilom pridruživanja $f (x) = x^{n}$ $f (x) = x^{n}$ pri čemu je $n$ $n$ bio paran broj. Što vrijedi za funkcije s neparnim eksponentom $n$ $n$ ? Ispitajte na primjeru funkcije $f (x) = x^{3} .$ $f (x) = x^{3} .$

Ako je $n$ $n$ neparan, vrijednosti $f (- x)$ $f (- x)$ i $f (x)$ $f (x)$ bit će suprotni brojevi, odnosno vrijedi $f (- x) = - f (x) .$ $f (- x) = - f (x) .$

Neparna funkcija

Za funkciju $f$ $f$ kažemo da je neparna ako je za svaki $x$ $x$ iz domene funkcije $f$ $f$ i $- x$ $- x$ u domeni i vrijedi $f (- x) = - f (x) .$ $f (- x) = - f (x) .$

Zadatak 2.

Promotrite elementarne funkcije: $f (x) = | x |,$ $f (x) = |x|,$ $g (x) = \sqrt{x},$ $g (x) = \sqrt{x},$ $h (x) = \frac{1}{x},$ $h (x) = \frac{1}{x},$ $i (x) = a^{x},$ $i (x) = a^{x},$ $j (x) = {log}_{a} x,$ $j (x) = \log_{a} x,$ $k (x) = sin x,$ $k (x) = \sin x,$ $l (x) = cos x,$ $l (x) = \cos x,$ $m (x) = tg x .$ $m (x) = tg x .$ Koje su od njih neparne?

Neparne su funkcije $f (x) = x,$ $f (x) = x,$ $h (x) = \frac{1}{x},$ $h (x) = \frac{1}{x},$ $k (x) = sin x,$ $k (x) = \sin x,$ $m (x) = tg x .$ $m (x) = tg x .$ Neparne su i sve potencije neparnoga eksponenta.

Primjer 2.

Provjerimo je li funkcija zadana s $f (x) = x^{3} + x^{2} sin x$ $f (x) = x^{3} + x^{2} \sin x$ neparna. Funkcija je definirana za svaki realni broj $x .$ $x .$

Računamo:

$\begin{matrix} f (- x) & = {(- x)}^{3} + {(- x)}^{2} sin (- x) = - x^{3} + x^{2} \cdot (- sin x) = = - x^{3} - x^{2} sin x = - (x^{3} + x^{2} sin x) = - f (x) \end{matrix} .$ $\begin{array}{ll} f (- x) & = {(- x)}^{3} + {(- x)}^{2} \sin (- x) = - x^{3} + x^{2} \cdot (- \sin x) = \\ = - x^{3} - x^{2} \sin x = - (x^{3} + x^{2} \sin x) = - f (x) \end{array} .$

Funkcija je neparna.

Zadatak 3.

Pokažite da je funkcija $f (x) = \frac{x + tg x}{x^{2}}$ $f (x) = \frac{x + tg x}{x^{2}}$ neparna.

$f (- x) = \frac{- x + tg (- x)}{{(- x)}^{2}} = \frac{- x - tg x}{x^{2}} = - \frac{x + tg x}{x^{2}} = - f (x)$

Graf neparne funkcije

Zadatak 4.

Promotrite grafove neparnih funkcija. Koje svojstvo uočavate? Pokažite da uočeno svojstvo vrijedi za sve neparne funkcije.

Graf neparne funkcije 1/2

Graf neparne funkcije 2/2

Za neparnu funkciju vrijedi $f (- x) = - f (x)$ pa se na grafu funkcije nalaze točke $(- x, y)$ i $(x, - y) .$ Graf funkcije je simetričan s obzirom na ishodište.

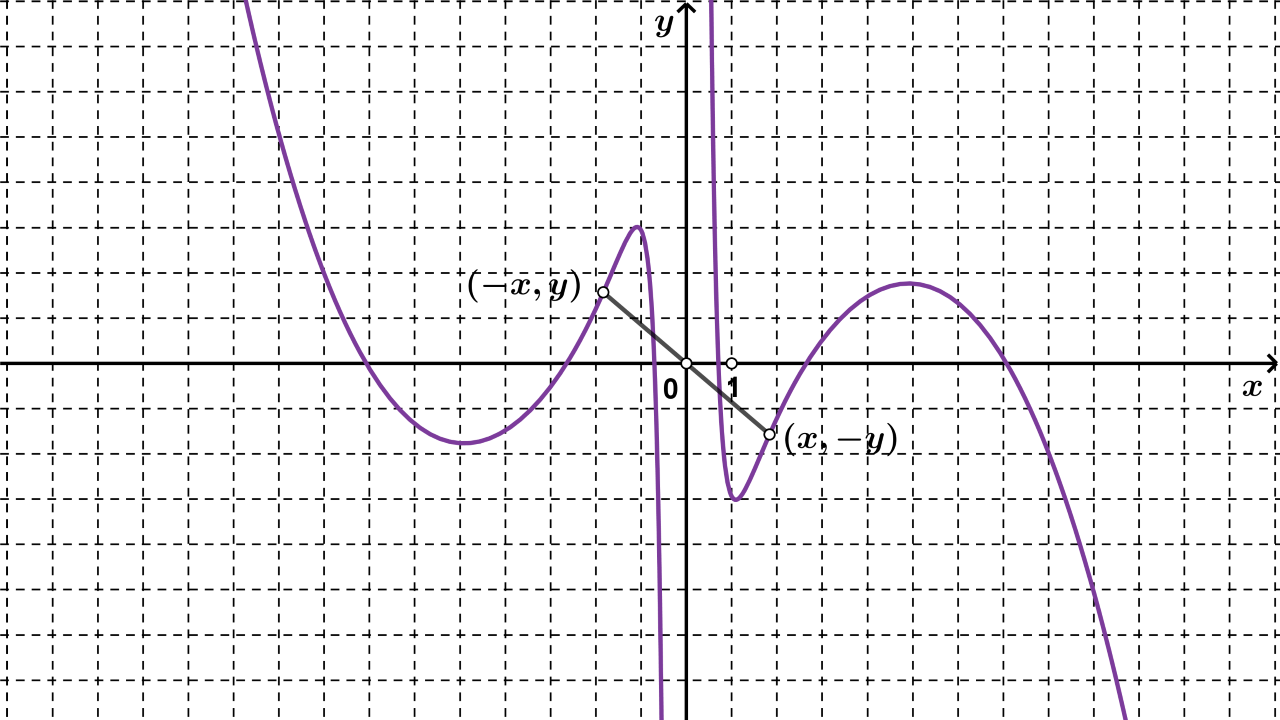
Graf neparne funkcije simetričan je s obzirom na ishodište.

Zadatak 5.

Označite grafove neparnih funkcija.

a.

b.

c.

d.

null

Zadatak 6.

Funkcija $f$ nije parna. Je li neparna?

Funkcija koja nije parna može, ali ne mora biti neparna. Mnoge funkcije nisu ni parne ni neparne. To možemo lako pokazati grafovima. Graf parne funkcije simetričan je s obzirom na os ordinata, graf neparne s obzirom na ishodište. Postoje grafovi koji nisu simetrični, na primjer graf funkcije $f (x) = x + 1 .$

Primjer 3.

Provjerimo je li parna ili neparna funkcija $f (x) = x^{2} + x .$ Odredimo $f (- x) :$

$f (- x) = {(- x)}^{2} + (- x) = x^{2} - x .$

Provjerimo parnost. Vidimo da je $f (- x) \neq f (x)$ pa funkcija nije parna.

Provjerimo neparnost. Budući da je $- f (x) = - x^{2} - x$ vidimo da je $f (- x) \neq - f (x)$ pa funkcija nije neparna.

Zaključujemo da funkcija nije niti parna niti neparna.

Kutak za znatiželjne

Neka su funkcije $f$ i $g$ parne. Što možemo zaključiti o funkcijama $f + g$ i $f \cdot g ?$

Što možemo zaključiti o zbroju i umnošku dviju neparnih funkcija? Što možemo zaključiti o zbroju i umnošku jedne parne i jedne neparne funkcije?

...i na kraju

Razvrstajte pravila pridruživanja prema parnosti/neparnosti.

$f (x) = x^{2} + x^{3}$

Parne funkcije

Neparne funkcije

Ni parne ni neparne

null

$x$ $x$	$- 3$ $- 3$	$- 2$ $- 2$	$- 1$ $- 1$	$1$ $1$	$2$ $2$	$3$ $3$
$f (x)$ $f (x)$ $=$ $=$ $x^{2}$ $x^{2}$
$g (x)$ $g (x)$ $=$ $=$ $x^{4}$ $x^{4}$

Na početku...

Potencije

Istražimo

Kolekcija zadataka #1

Parne funkcije

Parne funkcije

Zadatak 1.

Primjer 1.

Graf parne funkcije

Istražimo

Kolekcija zadataka #2

Neparne funkcije

Istražimo

Neparna funkcija

Zadatak 2.

Primjer 2.

Zadatak 3.

Graf neparne funkcije

Zadatak 4.

Zadatak 5.

Zadatak 6.

Primjer 3.

Kutak za znatiželjne

...i na kraju

Parne funkcije

Neparne funkcije

Ni parne ni neparne