Matematika 3 - 1.1 Potencije s racionalnim eksponentima

Na početku...

Što znači riječ KORIJEN?

Prisjetimo se uporabe te riječi u raznim područjima znanosti i života. Napišite na papir riječ KORIJEN i pojmove s kojima je povezana.

Pogledajte u nastavku animaciju s primjerima primjene te riječi.

Životne okolnosti uvjetovale su računanje potencija $($ npr. zakon poluraspada nekog elementa računamo formulom $N = N_{0} \cdot 2^{- \frac{t}{T_{1 / 2}}})$ i korijena $($ npr. određivanje duljine stranice pločice kvadratnog oblika kojoj znamo površinu, $a = \sqrt{P}) .$ Još su matematičari iz Babilona usporedno s tablicama za množenje napravili i tablice "obrnutih" veličina. Tablice "obrnutih" veličina prikazuju kvadratne korijene brojeva.

Rješavanjem sve složenijih algebarskih zadataka pojavila se potreba za uopćavanjem i proširivanjem pojma potencije prirodnih eksponenata, preko nule i negativnih brojeva, do eksponenata u obliku razlomaka.

U ovom modulu otkrit ćemo vezu potencija racionalnog eksponenta s korijenima višeg stupnja te naučiti računati s istima.

Povijesna oznaka korijena, slovo R s prekriženom crticom — Povijesna oznaka korijena

Zanimljivost

Na slici možete vidjeti staru oznaku za korijen. Simbol koji sliči slovu $R$ s prekriženom crticom. Ovu oznaku uvodi talijanski matematičar Leonardo Fibonacci iz Pise (oko 1175. - oko 1240.), još davne 1220. godine, kao oznaku za korijen. Simbol najvjerojatnije dolazi kao kratica $R$ od latinske riječi radix (korijen). Istražite povijesni razvoj znaka za korijen.

Prisjetimo se

Ponovimo značenje potencije te računanje s nulom i jedinicom.

Kolekcija zadataka #1

Povežite jednake izraze.

$1 \cdot a^{n} =$	$a$
$a^{0} =$	$a^{m}$
$a^{1} =$	$a^{n}$
$\underset{m faktora}{\underset{⏟}{a \cdot a \cdot . . . \cdot a}}$	$\frac{1}{a}$
$a^{- 1} =$	$1$

null

Povežite jednake izraze.

$3 \cdot 3 \cdot 3 \cdot 3$	$a^{5}$
$a \cdot a \cdot a \cdot a \cdot a$	$3^{4}$
$3^{4}$	$81$

null

Povežite jednake izraze.

${(\frac{1}{3})}^{4}$	${(\frac{1}{3})}^{4}$
$\frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3}$	$3^{- 4}$
$\frac{1}{3}$	$3^{- 1}$

null

Veza između potencija i korijena

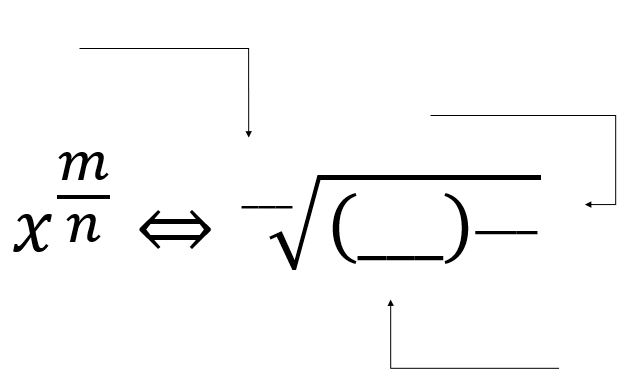
Povežimo oznake za potenciju i korijen. Istaknut je drugi korijen radi lakše poveznice s kvadratom. Inače se broj $2$ kod drugog korijena ne piše.

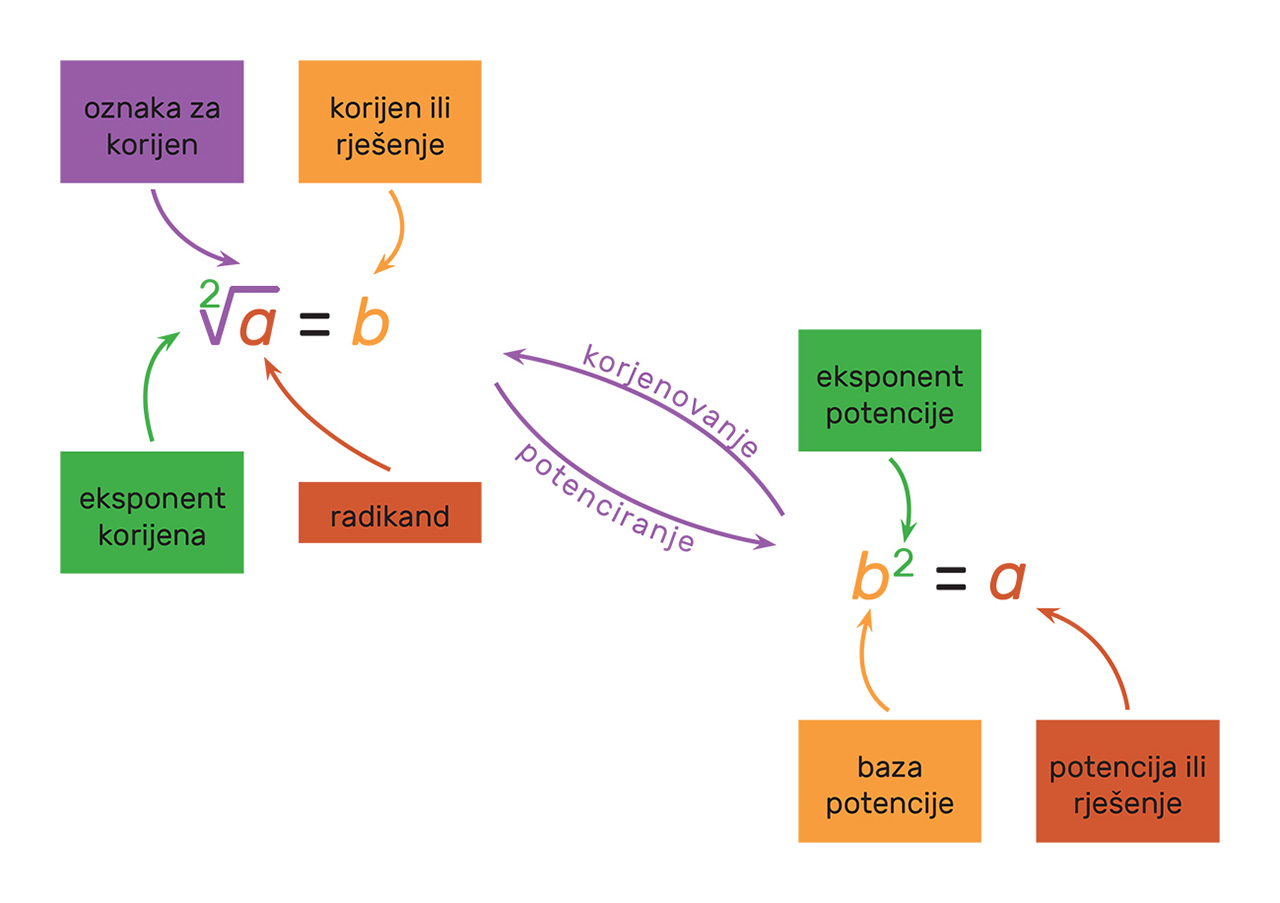
Oznake i nazivi korijena i potencije te njihova povezanost. — Veza korijena i potencije

Zadatak 1.

Pokušajte po analogiji s prethodnom ilustracijom napraviti vezu korijena i potencije s eksponentom $n .$

Oznake i nazivi korijena i potencije s eksponentom n te njihova povezanost. — Veza korijena i potencije s eksponentom n

Primjer 1.

Znamo da je $2^{4} = 16$ i pripadajući $4 .$ korijen je $\sqrt[4]{16} = 2 .$

Možemo li, koristeći se ovom vezom između potencija i korijena, izračunati $\sqrt[5]{32} ?$

$\sqrt[5]{32} = b \Leftrightarrow b^{5} = 32$

$b = 2$

Primjer 2.

Koristeći se vezom korijena i potencija, izraze na lijevoj strani jednakosti zapišimo kao potenciju ili korijen desne strane jednakosti.

$\sqrt[4]{a^{5}} = b$

$\sqrt[6]{\frac{3 x^{5}}{2 y^{2}}} = z$

${(\frac{3 a}{5})}^{4} = b$

${(7 x^{3})}^{5} = y$

U prva dva zadatka prikažimo jednakost pomoću potencije koristeći se vezom potencija i korijena.

$a^{5} = b^{4} .$

Možemo li sada prikazati nepoznanicu $a$ pomoću $b ?$

Uočimo da je eksponent uz $a$ jednak $5$ te jednadžbu korjenujemo tim eksponetom $(5 .$ korijenom). Dobijemo: $a = \sqrt[5]{b^{4}} .$
$\frac{3 x^{5}}{2 y^{2}} = z^{6} .$

Razmislite kako biste prikazali $x$ ili $y$ pomoću ostalih dviju nepoznanica.
$\frac{3 a}{5} = \sqrt[4]{b} .$

Čemu je jednako $a$ ?
$7 x^{3} = \sqrt[5]{y} .$

Prikažimo $x$ pomoću $y .$ Podijelimo dobivenu jednakost sa $7 .$ Kako je uz $x$ eksponent $3,$ jednadžbu korjenujemo $3 .$ korijenom i konačno imamo $x = \sqrt[3]{\frac{\sqrt[5]{y}}{7}} .$

Razmislimo!

Jesmo li mogli prethodni zadatak s dvostrukim korijenom riješiti drugačije? Kako izbjeći dva korijena?

Pokušajmo u nastavku pronaći odgovor na ta pitanja.

Pravila potenciranja

Ponovimo pravila potenciranja iz prvog razreda.

Pronađite parove tako da dobijete pravila potenciranja.

$a^{n} \cdot b^{n} =$	$a^{m \cdot n}$
$a^{n} : b^{n} =$	${(a \cdot b)}^{n}$
$a^{m} : a^{n} =$	$a^{m - n}$
$a^{m} \cdot a^{n} =$	$a^{m + n}$
${(a^{m})}^{n} =$	${(a : b)}^{n}$

null

Što s potencijom koja u eksponentu ima razlomak?

Primjer 3.

Primjenom pravila množenja potencija iste baze, izračunajmo:

$4^{\frac{1}{2}} \cdot 4^{\frac{1}{2}},$

$2^{\frac{1}{3}} \cdot 2^{\frac{1}{3}} \cdot 2^{\frac{1}{3}},$

$3^{\frac{1}{4}} \cdot 3^{\frac{1}{4}} \cdot 3^{\frac{1}{4}} \cdot 3^{\frac{1}{4}} .$

$4^{\frac{1}{2}} \cdot 4^{\frac{1}{2}} = 4^{\frac{1}{2} + \frac{1}{2}} = 4^{1} = 4,$
$2^{\frac{1}{3}} \cdot 2^{\frac{1}{3}} \cdot 2^{\frac{1}{3}} = 2^{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}} = 2,$
$3^{\frac{1}{4}} \cdot 3^{\frac{1}{4}} \cdot 3^{\frac{1}{4}} \cdot 3^{\frac{1}{4}} = 3^{\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4}} = 3 .$

Znamo da umnožak istih faktora možemo napisati kraće pomoću potencije pa za potenciju iz prethodnog zadatka vrijedi:

$4^{\frac{1}{2}} \cdot 4^{\frac{1}{2}} = {(4^{\frac{1}{2}})}^{2} = 4^{\frac{1}{2} \cdot 2} = 4 .$

S druge strane znamo da je ${(\sqrt{4})}^{2} = \sqrt{4} \cdot \sqrt{4} = 4 .$

Na isti način zaključite što vrijedi za preostala dva slučaja u prethodnom zadatku.

Možete li izvesti zaključak što predstavlja izraz $a^{\frac{1}{n}} ?$

Potražite jednake izraze.

$a^{\frac{1}{n}}$	$\sqrt[3]{2}$
$3^{\frac{1}{4}}$	$\sqrt[4]{3}$
$2^{\frac{1}{3}}$	$\sqrt{4}$
$4^{\frac{1}{2}}$	$\sqrt[n]{a}$

null

Dakle, eksponent $\frac{1}{n}$ u izrazu $a^{\frac{1}{n}}$ govori nam koliki je $n$ -ti korijen pozitivnog realnog broja $a$ . Odnosno, $n$ je broj kojim treba potencirati izraz $a^{\frac{1}{n}}$ kako bismo dobili bazu $a .$

Provjerite koliko ste razumjeli pojam potencije.

Množenje je skraćeno

Potenciranje je skraćeno

U potenciji

x^{r},

x

a racionalni broj $r$ je

x^{r}

računamo tako da, ako je cijeli broj

r > 0,

bazu

x

r

puta, odnosno ako je cijeli broj

r < 0,

broj

1

bazom pomnoženom

r

puta. Ako je

r = \frac{m}{n}

racionalni eksponent tada

x^{r}

računamo tako da bazu

x

m

te potenciju

x^{m}

n

-tim korijenom.

Primjenom pravila potenciranja potencije lako zaključujemo da je ${(x^{\frac{1}{n}})}^{m} = x^{\frac{1}{n} \cdot m} = x^{\frac{m}{n}} .$

Povežimo konačno potenciju s racionalnim eksponentom s pripadajućim korijenom.

Potencije s racionalnim eksponentom

Razmislite i odgovorite koji zapis pomoću korijena odgovara zadanoj potenciji.

Potencija $x^{\frac{m}{n}}$ može se zapisati i u obliku:

\sqrt{x^{\frac{m}{n}}}

Ne radi se o drugom (kvadratnom) korijenu.

\sqrt[m]{x^{n}}

Razmislite, koje je slovo u nazivniku eksponenta?

\sqrt[n]{x^{m}}

Bravo, odlično ste zaključili.

\sqrt[x]{\frac{m}{n}}

$x$ je baza pa nikako ne može biti eksponent korijena.

null

Za realni broj $x,$ $x \geq 0,$ cijeli broj $m$ i prirodni broj $n,$ $n \geq 2$ vrijedi $x^{\frac{m}{n}} = \sqrt[n]{x^{m}} .$

Za potencije s racionalnim eksponentima vrijede ista pravila kao i za potencije s cijelim eksponentima.

Riješite zadatke koristeći se pravilima potenciranja.

Kolekcija zadataka #2

Pomnožite.

$a^{\frac{2}{3}} \cdot a^{- \frac{1}{2}}$
$9^{\frac{5}{2}} \cdot 9^{- \frac{1}{2}}$

$a^{\frac{2}{3} - \frac{1}{2}} = a^{\frac{1}{6}}$
$9^{2} = 81$

Podijelite.

$b^{- \frac{3}{4}} : b^{- \frac{1}{2}}$
$4^{\frac{7}{3}} : 4^{- \frac{2}{3}}$

$b^{- \frac{1}{4}} = \frac{1}{b^{\frac{1}{4}}}$
$4^{\frac{7}{3} + \frac{2}{3}} = 4^{3} = 64$

Potencirajte.

${(x^{\frac{3}{2}})}^{\frac{1}{6}}$
${(y^{\frac{1}{2}} \cdot z^{- \frac{3}{4}})}^{\frac{4}{3}}$

$x^{\frac{1}{4}}$
$y^{\frac{1}{2} \cdot \frac{4}{3}} \cdot z^{- \frac{3}{4} \cdot \frac{4}{3}} = y^{\frac{2}{3}} \cdot z^{- 1} = \frac{y^{\frac{2}{3}}}{z}$

Korijeni ili potencije?

Primjer 4.

Prikažimo izraz ${(\frac{2}{3})}^{- \frac{1}{4}}$ pomoću korijena.

Najprije se riješimo negativnog eksponenta: ${(\frac{2}{3})}^{- \frac{1}{4}} = {(\frac{3}{2})}^{\frac{1}{4}} .$

Sada ćemo lako primijeniti prikaz pomoću korijena: ${(\frac{3}{2})}^{\frac{1}{4}} = \sqrt[4]{\frac{3}{2}} .$

Primjer 5.

Prikažimo izraz $\sqrt[3]{12 x^{6} y^{9}}$ pomoću potencije.

Najprije 3. korijen pretvorimo u racionalni eksponent: $\sqrt[3]{12 x^{6} y^{9}} = {(12 x^{6} y^{9})}^{\frac{1}{3}} .$

Primijenimo pravilo potenciranja potencije i skratimo razlomak u eksponentu do kraja.

${(12 x^{6} y^{9})}^{\frac{1}{3}} = 12^{\frac{1}{3}} \cdot x^{6 \cdot \frac{1}{3}} \cdot y^{9 \cdot \frac{1}{3}} = 12^{\frac{1}{3}} \cdot x^{2} \cdot y^{3} .$

U sljedećim zadatcima primijenite prikaz potencija pomoću korijena ili obrnuto.

Kolekcija zadataka #3

Uparite potenciju s pripadajućim korijenom.

$3^{\frac{2}{3}}$	$\sqrt[5]{x^{3}}$
$x^{\frac{5}{3}}$	$\sqrt[5]{3}$
$3^{\frac{1}{5}}$	$\sqrt[3]{9}$
$5^{\frac{1}{3}}$	$\sqrt[2]{27}$
$3^{\frac{3}{2}}$	$\sqrt[3]{x^{5}}$
$x^{\frac{3}{5}}$	$\sqrt[3]{5}$

null

Pretvorite korijen u potenciju i izračunajte sljedeće izraze. Konačno rješenje prikažite u obliku korijena.

$\sqrt[3]{9} : \sqrt[]{3}$
$\sqrt[3]{\sqrt[]{64}}$
$16 \cdot 8^{\frac{1}{3}} \cdot \sqrt[3]{2} \cdot 4^{- \frac{1}{2}}$

$\sqrt[3]{9} : \sqrt{3} = {(3^{2})}^{\frac{1}{3}} : 3^{\frac{1}{2}} = 3^{\frac{2}{3} - \frac{1}{2}} = 3^{\frac{1}{6}} = \sqrt[6]{3}$
$\sqrt[3]{\sqrt{64}} = {({(2^{6})}^{\frac{1}{2}})}^{\frac{1}{3}} = 2^{6 \cdot \frac{1}{2} \cdot \frac{1}{3}} = 2$
$16 \cdot 8^{\frac{1}{3}} \cdot \sqrt[3]{2} \cdot 4^{- \frac{1}{2}} = 2^{4} \cdot 2^{3 \cdot \frac{1}{3}} \cdot 2^{\frac{1}{3}} \cdot 2^{2 \cdot (- \frac{1}{2})} =$

$= 2^{4 + 1 + \frac{1}{3} - 1} = 2^{\frac{13}{3}} = \sqrt[3]{2^{13}} = \sqrt[3]{2^{12} \cdot 2} = 16 \sqrt[3]{2}$

Zadane izraze prikažite u obliku korijena, bez negativnog eksponenta.

${(\frac{x}{2})}^{- 1.5}$
${(x^{2} - y^{2})}^{\frac{1}{2}}$
${(8 - b^{3})}^{- \frac{5}{3}}$

$\sqrt{\frac{8}{x^{3}}}$
$\sqrt{x^{2} - y^{2}}$
$\frac{1}{\sqrt[3]{{(8 - b^{3})}^{5}}}$

Koristeći se pravilima potenciranja uspješno smo riješili složenije zadatke s korijenom.

Zadatak 2.

Vratite se na Primjer 2.d) ${(7 x^{3})}^{5} = y$ i prikažite broj $x$ pomoću $y$ uz pomoć samo jednog korijena.

$7^{5} {(x^{3})}^{5} = y \Rightarrow x^{15} = \frac{y}{7^{5}} \Rightarrow x = \sqrt[15]{\frac{y}{7^{5}}}$

...i na kraju

Možemo li odgovoriti na pitanje: korijeni ili potencije?

Prikaz korijena pomoću potencija iskoristili smo za rješavanje složenijih zadataka s korijenom. No, mogu li korijeni bez potencija? Postoje li možda neka pravila i za računanje s korijenima?

Na to pitanje potražite odgovor u sljedećim jedinicama.

Prije nastavka ponovimo još jedanput što smo naučili o prikazu korijena pomoću potencije.

Složite oznake i nazive na mjesta označena crtom.

Veza potencija i korijena (predložak za dopunjavanje s oznakama i nazivima)

m

n

x

eksponent korijena

eksponent potencije

radikand

null