Matematika 3 - Aktivnosti za samostalno učenje

Na početku...

Ne bi li se glazba mogla opisati kao matematika osjećaja, a matematika kao glazba uma?

James Sylvester (1814. - 1897.)

Ovako je matematiku doživio James Sylvester, engleski matematičar s kraja 19. stoljeća (bavio se teorijom brojeva) i profesor matematike u Oxfordu.

Pokušajmo i mi zasvirati s matematikom.

Engleski matematičar James Sylvester — James Sylvester

Matematika i glazba

Korelacija

Glazbena ljestvica je niz tonova razvrstanih u oktave. Oktava je glazbeni interval od osam tonova. Svaka viša oktava ima dvostruko veću frekvenciju od niže. Omjer frekvencije bilo kojih dvaju titraja koji proizvode oktavu iznosi $1 : 2 .$ Između tih dvaju tonova frekvencije u pravilu razlikujemo $12$ polutonova.

Ako između dviju bijelih tipaka imamo crnu, govorimo o cijelom tonu, a ako crne nema, govorimo o polutonu.

Ako osnovni ton ima frekvenciju $x,$ sljedeći ton za oktavu više ima frekvenciju $2 x .$ Manji intervali od oktave jesu kvinta i kvarta.

Istražimo

Istražite što su kvinta, kvarta i oktava. Što je dur i mol? Doznajte više o pitagorejskoj ljestvici. Nakon što se upoznate s ovim osnovnim pojmovima, pokušajte otkriti kakve glazba ima veze s $\sqrt[12]{2} .$

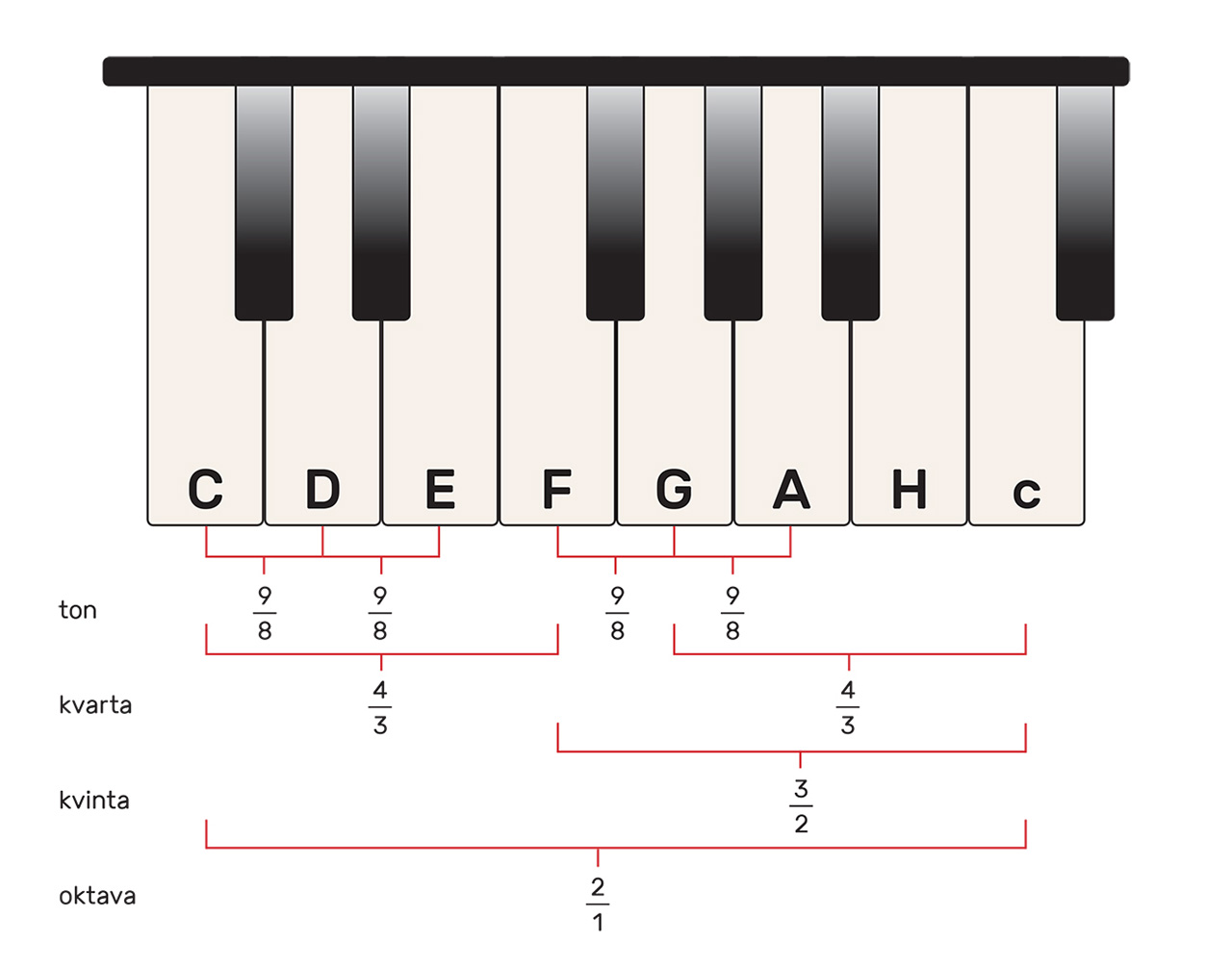
Pogledajmo sljedeću podjelu tonova jedne oktave.

Oktava s 12 tonova (7 bijelih tipki i 5 crnih) i pripadajućim intervalima (ton, kvarta, kvinta, oktava) — Oktava s 12 tonova i pripadajućim intervalima

Fotografija koja prikazuje Pitagoru. — Pitagorina bista u rimskom muzeju Capitolini

Zanimljivost

Prolazeći ispred radionice kovača, Pitagora je slušajući udarce o nakovanj raspoznao intervale kvarte, kvinte i oktave. Pretpostavljajući da su razlike u zvukovima povezane s veličinom čekića, izmjerio je njihovu masu i otkrio da je onaj koji je proizvodio oktavu upola lakši od najtežeg, onaj koji je proizvodio kvintu za dvije trećine lakši, a onaj koji je proizvodio kvartu za tri četvrtine lakši.

Pričvrstivši strunu na monokord i podijelivši je na četiri jednaka dijela, otkrio je da pri proizvodnji zvuka tri dijela strune i jedna polovina daju interval kvinte; cijela struna i struna pričvršćena na tri četvrtine interval kvarte; struna i njezina polovina interval oktave.

Istražite više o Pitagorinoj ljestvici.

Uzmimo da je frekvencija osnovnog tona C jednaka $x$ . Postavite zadane frekvencije na pravo mjesto u danoj oktavi.

\frac{9}{8} x

\frac{27}{16} x

\frac{4}{3} x

\frac{243}{128} x

\frac{81}{64} x

\frac{3}{2} x

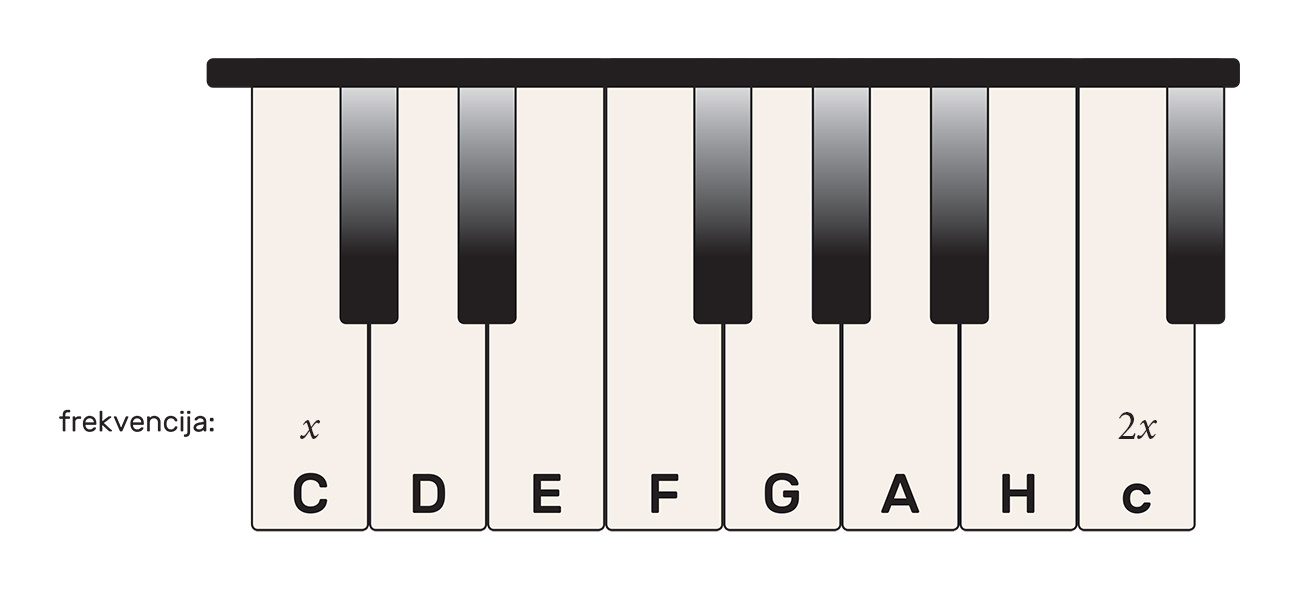
Pomoć:

Omjere postavite iznad slova.

Postupak:

Pogledajte u prethodnoj ilustraciji veličine tonova, kvarte, kvinte i oktave te postavite zadane omjere. Npr. za ton A vrijedi da je omjer $\frac{A}{G} = \frac{9}{8} i \frac{G}{C} = \frac{3}{2} \Rightarrow \frac{A}{C} = \frac{9}{8} \cdot \frac{3}{2} = \frac{27}{64} \Rightarrow A= \frac{27}{64} x .$

Što ako je ljestvica u nekom drugom duru? Pokušajmo odrediti frekvenciju susjednih tonova ako je prvi ton ljestvice "D". S obzirom na to da je omjer između dvaju susjednih tonova uvijek jednak, a ton "D" ima frekvenciju $\frac{9}{8} x,$ ton nakon njega ("E") mora biti $\frac{9}{8}$ puta veći. Dakle, u novom duru, ton "E" ima frekvenciju $\frac{9}{8} \cdot \frac{9}{8} x = \frac{81}{64} x .$

Kolekcija zadataka #1

Kolika je razlika između frekvencije tona "D" u C-duru u odnosu na D-dur? (Zaokružite rezultat na $4$ decimale.)

\frac{81}{64} - \frac{5}{4} =

Podijelite svaki razlomak pa oduzmite rezultat.

Dakle, razlika je zanemarivo malena, ali ipak postoji.
Kako odrediti isti ton s različitim frekvencijama? Rješenje je u tome da se razmak između dviju oktava ne podijeli na

7,

već na

12

tonova i to tako da je omjer između susjednih dvaju tonova uvijek jednak. Podjelu na

12

tonova (polustepena) označavaju crne tipke na klavijaturi.

null

Pokušajmo otkriti koliki je taj omjer.
Neka je početna frekvencija osnovnog (prvog) tona u oktavi jednaka

, dok ton za oktavu više (visoki osnovni ton) ima frekvenciju

. Između osnovnog i visokog tona (unutar jedne oktave) ima

polustepenskih razmaka i svi imaju

omjer ili kvocijent, $k .$

12

isti

x

2 x

null

Budući da se kvocijent (omjer) dvaju susjednih tonova (polustepena) od osnovnog tona oktave do visokog početnog tona oktave ponavlja $12$ puta, možemo reći da je kvocijent između njih jednak

12 \cdot k

Pripazite, radi se o umnošku

12

omjera, a ne zbrajanju svih omjera dvaju susjednih polutonova.

12 + k

Pripazite,

12

puta ponavljamo isti omjer, k susjednih polutonova.

\frac{12}{k}

k^{12}

12^{k}

Razmislite, ponavlja li se

12 .

k

puta ili se omjer $k$ ponavlja

12

puta?

null

Omjer frekvencija osnovnog i visokog početnog tona između kojih je $12$ tonova (polustepenskih razmaka) iznosi:

\frac{2 x}{x} = k

Pripazite, između dva početna tona, odnosno u jednoj oktavi je

12

jednakih omjera.

\frac{2 x}{x} = 12 k

Pripazite,

12

puta imamo isti omjer (ne zbrajamo ga

12

puta).

\frac{2 x}{x} = k^{12}

Bravo!

\frac{2 x}{x} = 12^{k}

Pripazite, nemamo

k

puta omjer veličine

12 .

null

Konačno možemo odgovoriti na pitanje koliki je omjer između susjednih polustepenskih razmaka u oktavi.

Ako s $k$ označimo omjer između sujednih tonova u oktavi podijeljenoj na $12$ tonova, tada vrijedi:

k = \sqrt[12]{2}

k = 2^{12}

k = \sqrt{12}

k = 2 \cdot 12 = 24

null

Potencije racionalnog eksponenta u nazivniku

Naučili smo racionalizirati nazivnik s $n$ -tim korijenom.

Pogledajmo kako se riješiti racionalnog eksponenta u nazivniku.

Primjer 1.

Racionalizirajmo nazivnik razlomka $\frac{x}{y z^{\frac{1}{2}}} .$

1. način

Potenciju zapišimo u obliku korijena i racionalizirajmo po već poznatom pravilu: $\frac{x}{y z^{\frac{1}{2}}} = \frac{x}{y \sqrt{z}} \cdot \frac{\sqrt{z}}{\sqrt{z}} = \frac{x \sqrt{z}}{y z} .$

2. način

Pokušajmo dobiti isti rezultat bez primjene korijena. Uočimo da je $\sqrt{z} = z^{\frac{1}{2}} .$

$\frac{x}{y z^{\frac{1}{2}}} \cdot \frac{z^{\frac{1}{2}}}{z^{\frac{1}{2}}} = \frac{x z^{\frac{1}{2}}}{y z}$

Zadatak 3.

Racionalizirajte nazivnik i konačno rješenje prikažite u obliku korijena.

$\frac{8}{15 \cdot 2^{\frac{7}{3}}}$
$\frac{n}{n^{\frac{1}{n}}}$

$\frac{8}{15 \cdot 2^{\frac{7}{3}}} = \frac{8}{15 \cdot 2^{2} \cdot 2^{\frac{1}{3}}} \cdot \frac{2^{\frac{2}{3}}}{2^{\frac{2}{3}}} = \frac{8 \cdot 2^{\frac{2}{3}}}{15 \cdot 2^{3}} = \frac{2^{\frac{2}{3}}}{15} = \frac{\sqrt[3]{4}}{15}$
$n^{\frac{n - 1}{n}} = \sqrt[n]{n^{n - 1}}$

Kutak za znatiželjne

Racionalizirajmo nazivnik.

$\frac{a - 1}{a^{\frac{1}{2}} - 1}$
$\frac{x + y}{x^{\frac{1}{3}} + y^{\frac{1}{3}}}$

Pogledajte video o tome kako riješiti ove zadatke.

Zadatak 4.

Racionalizirajte nazivnik.

$\frac{7^{\frac{1}{2}} + 3^{\frac{1}{2}}}{7^{\frac{1}{2}} - 3^{\frac{1}{2}}}$
$\frac{1}{1 - {(\frac{1}{2})}^{\frac{1}{3}}}$

$\frac{5 + 21^{\frac{1}{2}}}{2}$
Uputa: broj $1$ može se prikazati u obliku bilo koje potencije (može se prilagoditi zadatku). Ovdje primjećujemo da vrijedi: $1 - {(\frac{1}{2})}^{\frac{1}{3}} = 1^{\frac{1}{3}} - {(\frac{1}{2})}^{\frac{1}{3}} .$
Rješenje: $2 + 2^{\frac{2}{3}} + 2^{\frac{1}{3}}$

...i na kraju

Prošle ste se godine upoznali s iracionalnim jednadžbama koje se svode na linearne ili kvadratne jednadžbe.

Pogledajmo za kraj kako riješiti jednadžbe racionalnog eksponenta.

Iracionalne jednadžbe

Iracionalne jednadžbe su jednadžbe u kojima nepoznanica dolazi u bazi potencije s racionalnim eksponentom.

Primjeri iracionalnih jednadžbi: $x^{\frac{1}{2}} = 5$ ; ${(x^{2} + 1)}^{\frac{1}{2}} = 4$ ; $3 x^{\frac{1}{2}} + 2 x^{\frac{1}{2}} = x + 1$ ili $x^{- \frac{1}{2}} + {(x + 1)}^{\frac{1}{2}} = x + 2 .$

Ponuđene jednadžbe razvrstajte po tipovima.

1 + 5^{- 2} x^{2} + 25^{- \frac{1}{2}} x = 0

2^{2} x - 32^{\frac{1}{5}} = 4^{\frac{1}{2}}

2 x + 3 x^{\frac{1}{2}} = 1

64 x^{- 2} + x = 0

x^{2} + 16 = 64^{\frac{1}{2}} x

{(x - 3)}^{3} = 27

x^{\frac{1}{2}} - x + 1 = 0

x^{\frac{1}{3}} - \frac{1}{3} = 0

1 + 8^{\frac{1}{3}} x = x

(x + 1) (x^{\frac{1}{2}} - x) = 0

3^{\frac{1}{2}} x^{2} = 5^{\frac{1}{2}}

Iracionalne jednadžbe

Kvadratne jednadžbe

Linearne jednadžbe

Ostale jednadžbe

null

Primjer 2.

Riješimo iracionalnu jednadžbu $x^{\frac{1}{3}} + 2 x^{\frac{2}{3}} - 3 = 0 .$

Zadatak možemo riješiti metodom supstitucije: $x^{\frac{1}{3}} = t \Rightarrow t + 2 t^{2} - 3 = 0 \Rightarrow 2 t^{2} + t - 3 = 0 .$

Rješavanjem kvadratne jednadžbe dobije se: $t_{1} = 1,$ $t_{2} = - \frac{3}{2} .$
Dakle, $x^{\frac{1}{3}} = 1 (ili \sqrt[3]{x} = 1) \Rightarrow x_{1} = 1^{3} = 1 .$
Provjerimo rješenje uvrštavanjem u početnu jednadžbu.
$1^{\frac{1}{3}} + 2 \cdot 1^{\frac{2}{3}} - 3 = 0 \Rightarrow 3 - 3 = 0 \Rightarrow 0 = 0 .$
Kako je jednakost točna, $1$ je rješenje početne jednadžbe.

Provjerimo drugo rješenje.

$x^{\frac{1}{3}} = - \frac{3}{2} (ili \sqrt[3]{x} = - \frac{3}{2}) \Rightarrow x_{2} = {(- \frac{3}{2})}^{3} = - \frac{27}{8} .$
Uvrstimo u početnu jednadžbu.
${(- \frac{27}{8})}^{\frac{1}{3}} + 2 \cdot {(- \frac{27}{8})}^{\frac{2}{3}} - 3 = 0 \Rightarrow$

${(- \frac{3^{3}}{2^{3}})}^{\frac{1}{3}} + 2 \cdot {(- \frac{3^{3}}{2^{3}})}^{\frac{2}{3}} - 3 = 0 \Rightarrow$

- \frac{3}{2} + 2 \cdot \frac{9}{4} - 3 = 0 \Rightarrow 3 - 3 = 0 \Rightarrow 0 = 0 .

Zaključujemo da je i $- \frac{27}{8}$ rješenje početne jednadžbe.
Kako ne postoje uvjeti na radikanda $(x \in R)$ jer je eksponent korijena neparan, rješenja jednadžbe su: $x_{1} = 1 i x_{2} = - \frac{27}{8} .$

$\frac{3}{\sqrt{2}}$	$\frac{1 + \sqrt{2}}{1 + \sqrt{2}}$
$\frac{1}{1 - \sqrt{2}}$	$\frac{\sqrt[3]{2}}{\sqrt[3]{2}}$
$\frac{2}{\sqrt[3]{2}}$	$\frac{\sqrt[3]{4}}{\sqrt[3]{4}}$
$\frac{3}{1 + \sqrt{2}}$	$\frac{\sqrt{2}}{\sqrt{2}}$
$\frac{\sqrt{2}}{\sqrt{3}}$	$\frac{\sqrt{3}}{\sqrt{3}}$
$\frac{\sqrt{2}}{\sqrt[3]{4}}$	$\frac{1 - \sqrt{2}}{1 - \sqrt{2}}$

$(x - y) (x + y) = x^{2} - y^{2}$
${(x \pm y)}^{2} = x^{2} \pm 2 x y + y^{2}$
$(x - y) (x^{2} + x y + y^{2}) = x^{3} - y^{3}$
$(x + y) (x^{2} - x y + y^{2}) = x^{3} + y^{3}$
${(x \pm y)}^{3} = x^{3} \pm 3 x^{2} y + 3 x y^{2} \pm y^{3}$

1.5 Aktivnosti za samostalno učenje

Na početku...

Matematika i glazba

Korelacija

Istražimo

Zanimljivost

Kolekcija zadataka #1

Racionalizacija nazivnika

Racionalizacija nazivnika

Kolekcija zadataka #2

Kolekcija zadataka #3

Kolekcija zadataka #4

Zadatak 1.

Zadatak 2.

Potencije racionalnog eksponenta u nazivniku

Primjer 1.

Zadatak 3.

Kutak za znatiželjne

Zadatak 4.

...i na kraju

Iracionalne jednadžbe

Iracionalne jednadžbe

Kvadratne jednadžbe

Linearne jednadžbe

Ostale jednadžbe

Primjer 2.