Matematika 3 - 6.1 Rješavanje trigonometrijskih jednadžbi pomoću brojevne kružnice

Na početku...

Slika trigonometrijskih operacija na školskoj ploči. — Trigonometrija u školi

Trigonometrijske funkcije definirali smo pomoću brojevne kružnice. Svakom realnom broju $t$ pridružili smo jednu točku na kružnici. Koordinate te točke predstavljaju vrijednost kosinusa, odnosno sinusa. Tu istu kružnicu iskoristimo kako bismo za danu vrijednost trigonometrijske funkcije pronašli pripadajući kut, odnosno sve realne brojeve koje zadovoljavaju zadanu trigonometrijsku vrijednost.

Pokrenite sljedeću animaciju te uočite koje vrijednosti broja $t$ možemo pridružiti odabranoj vrijednosti sinusa ili kosinusa na intervalu $[0,2 π⟩$ .

Ponovimo

Postavite oznake na odgovarajuću crtu.

x

tg x

ctg x

\sin x

(1, 0)

\cos x

(0, 1)

null

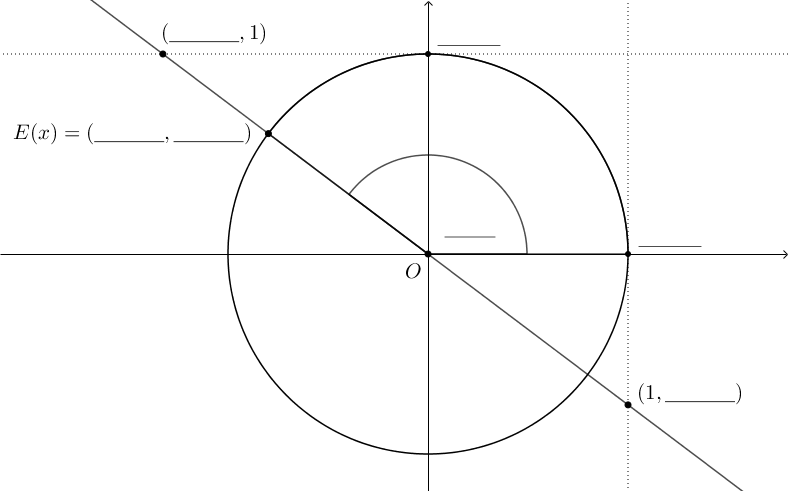
Pridružite pojmove o mjeri kuta pripadajućem svojstvu.

Glavna mjera kuta	$x = x_{0} + 2 k π, k \in Z$
Sve mjere kuta	$x_{0} \in [0, 2 π⟩$

null

Pridružite trigonometrijske funkcije pripadajućim osima na kojima očitavamo njihove vrijednosti.

$\sin x$
$\cos x$
$tg x$
$ctg x$

null

Pridružite trigonometrijske funkcije pripadajućoj domeni.

$ctg x$	$R \ \{\frac{π}{2} + k π, k \in Z\}$
$tg x$	$R \ \{k π, k \in Z\}$
$\sin x, \cos x$	$R$

null

Rasporedite trigonometrijske funkcije s obzirom na pripadajući skup vrijednosti.

tg x

\cos x

ctg x

\sin x

$[- 1, 1]$

$R$

null

Elementarne trigonometrijske jednadžbe

Trigonometrijske jednadžbe

Trigonometrijske jednadžbe jesu jednadžbe u kojima se nepoznanica pojavljuje kao argument neke trigonometrijske funkcije.

Trigonometrijska jednadžba, ako je dobro definirana, na skupu $R$ ima beskonačno mnogo rješenja.

Odredimo rješenja osnovnih trigonometrijskih jednadžbi pomoću brojevne kružnice, glavne mjere kuta, odnosno svojstva periodičnosti.

Zadatak 1.

Za koji će realni broj $a$ elementarna trigonometrijska funkcija imati rješenja?

$\sin x = a$
$\cos x = a$
$tg x = a$
$ctg x = a$

$a \in [- 1, 1]$
$a \in [- 1, 1]$
$a \in R$
$a \in R$

Primjer 1.

Uz pomoć brojevne kružnice riješimo jednadžbu: $\sin x = - \frac{1}{2} .$

Riješimo zadatak uz pomoć brojevne kružnice. S obzirom na to da vrijednost sinusa čitamo na osi ordinata, ovaj zadatak možemo svesti na traženje presjeka brojevne kružnice s pravcem: $y = - \frac{1}{2} .$

Rješenja iz grafičkog prikaza jesu: $x_{1} = \frac{7 π}{6}$ i $x_{2} = \frac{11 π}{6} .$ To su glavne mjere kuta.

Sve mjere ovih kutova čine sva rješenja zadane jednadžbe.

$\{\frac{7 π}{6} + 2 k π : k \in Z\}$ i $\{\frac{11 π}{6} + 2 k π : k \in Z\} .$

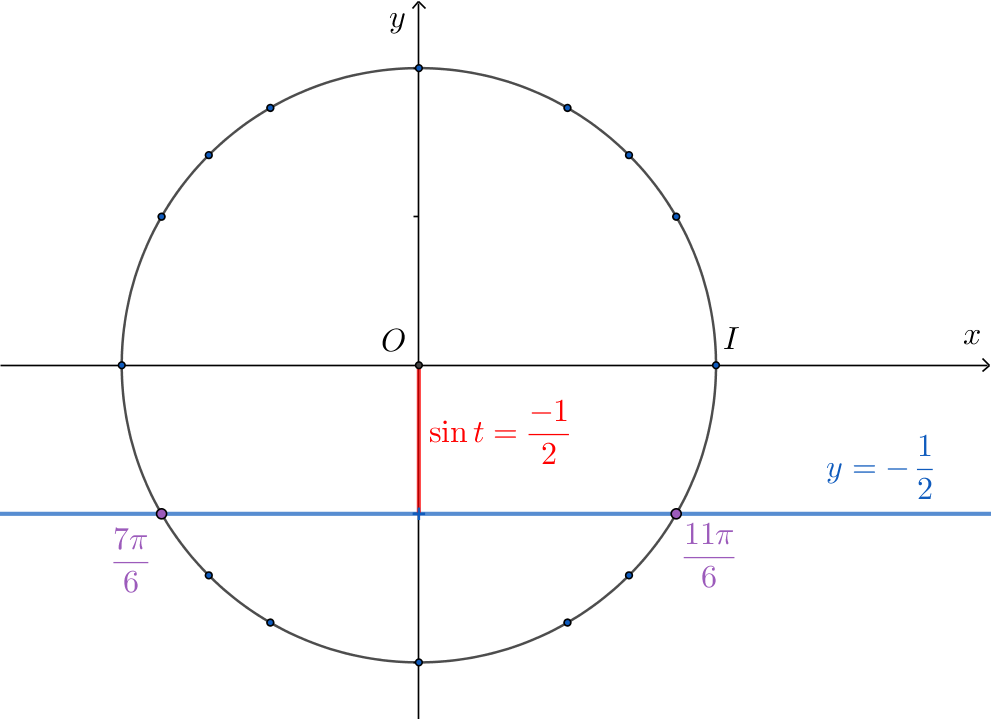
Grafičko rješenje primjera 1. — Rješenje jednadžbe pomoću brojevne kružnice

S obzirom na to da se ne traži samo glavna mjera kuta, već skup svih rješenja, drugu smo vrijednost mogli zapisati i pomoću negativnog realnog broja, pa rješenja možemo zapisati i u obliku: $\{\frac{7 π}{6} + 2 k π : k \in Z\}$ i $\{- \frac{π}{6} + 2 k π : k \in Z\} .$

Uočavate li vezu između brojeva $x_{1}$ i $x_{2} ?$

Vrijedi: $x_{1} + x_{2} = π .$

Analogno riješite zadatke s ostalim elementarnim trigonometrijskim funkcijama.

Kolekcija zadataka #1

Riješite jednadžbu: $\cos x = \frac{\sqrt{3}}{2} .$

$x_{1} = \frac{π}{6}, x_{2} = - \frac{π}{6},$ sva rješenja

$\{\pm \frac{π}{6} + 2 k π : k \in Z\} .$

1. grafičko rješenje Kolekcije zadataka 1 — Rješenje jednadžbe pomoću brojevne kružnice

Riješite jednadžbu: $tg x = \sqrt{3} .$

$x = \frac{π}{3} .$ Drugo je rješenje uvećano za $π$ pa je dovoljno napisati jedno rješenje uz pomoć kojega možemo prikazati sva rješenja: $\{\frac{π}{3} + k π : k \in Z\} .$

2. grafičko rješenje Kolekcije zadataka 1 — Rješenje jednadžbe pomoću brojevne kružnice

Riješite jednadžbu: $ctg x = - \sqrt{3} .$

$x = \frac{5 π}{6}$

Sva rješenja možemo kraće zapisati ovako: $x = \frac{5 π}{6} + k π, k \in Z .$

3. grafičko rješenje Kolekcije zadataka 1 — Rješenje jednadžbe pomoću brojevne kružnice

Trigonometrijske jednadžbe oblika Asin(bx+c)+d=0 i Acos(bx+c)+d=0

Trigonometrijsku jednadžbu oblika $A \sin (b x + c) + d = 0$ napišimo u obliku: $\sin (b x + c) = - \frac{d}{A} .$

Iz ovakvog zapisa rješenje možemo odrediti na brojevnoj kružnici.

Primjer 2.

Uz pomoć brojevne kružnice riješimo jednadžbu: $2 \sin (\frac{x}{2} - \frac{π}{3}) - \sqrt{2} = 0 .$

Nakon sređivanja, jednadžba ima oblik: $\sin (\frac{x}{2} - \frac{π}{3}) = \frac{\sqrt{2}}{2} .$

Kako do kraja riješiti jednadžbu, pogledajte u sljedećem videu.

Riješimo prethodni primjer pomoću interaktivne brojevne kružnice.

Odaberimo najprije tip trigonometrijske jednadžbe. Pomičući plavu točku pomičimo pravac dok ne dobijemo $y = \frac{\sqrt{2}}{2} .$ Pročitajmo presjek kružnice i pravca.

Presjek s kružnicom daje nam rješenja koja izjednačimo s argumentom funkcije sinus te riješimo zadatak do kraja kao što je pokazano u prethodnom videu.

Ovakva interaktivna kružnica može nam pomoći u dobivanju rješenja koja nisu poznata iz tablica.

Riješimo sljedeći zadatak uz pomoć interaktivne kružnice.

Primjer 3.

Riješimo jednadžbu: $- \frac{1}{2} \cos (3 x + \frac{π}{12}) + \frac{1}{3} = 0 .$

$\cos (3 x + \frac{π}{12}) = \frac{2}{3} \Rightarrow 3 x + \frac{π}{12} = 0.8411$

Ovo smo rješenje pročitali na interaktivnoj brojevnoj kružnici. Sada do kraja riješimo linearnu jednadžbu vodeći računa o svim rješenjima trigonometrijske jednadžbe.

Budući da vrijedi $3 x + \frac{π}{12} = \pm 0.8411 + 2 k π,$ sva su rješenja sljedeća: $x_{1} = 0.1931 + \frac{2 k π}{3}, k \in Z$ i $x_{2} = - 0.3676 + \frac{2 k π}{3}, k \in Z .$

Zadatak 2.

Uz pomoć interaktivne kružnice riješite trigonometrijske jednadžbe.

$\frac{1}{2} \sin (2 x + \frac{π}{3}) - \frac{1}{4} = 0$
$\sqrt{2} \cos (0.5 x - \frac{π}{6}) - 1 = 0$
$5 \sin (\frac{x}{3} + \frac{π}{8}) - 4 = 0$
$- \sqrt{3} \cos (1.5 x - \frac{π}{9}) - \sqrt{2} = 0$
$\sin (x - \frac{π}{2}) - 2 = 0$

$x_{1} = - \frac{π}{12} + k π, k \in Z$ i $x_{2} = \frac{π}{4} + k π, k \in Z .$
$x_{1} = \frac{5 π}{6} + 4 k π, k \in Z$ i $x_{2} = - \frac{π}{6} + 4 k π, k \in Z .$
$x_{1} = 1.6 + 6 k π, k \in Z$ i $x_{2} = 5.5 + 6 k π, k \in Z .$
$x_{1} = 1.9 + \frac{4 k π}{3}, k \in Z$ i $x_{2} = - 1.45 + \frac{4 k π}{3}, k \in Z .$
Nema rješenja.

...i na kraju

Ponovimo na kraju kako odrediti sva rješenja trigonometrijskih jednadžbi s obzirom na funkciju kojom su zadane.

Označimo s $x_{0}$ jedno rješenje trigonometrijske jednadžbe iz intervala $[0,2 π] .$ Sva rješenja kraće možemo zapisati bez skupovnih oznaka.

Trigonometrijska funkcija	Moguća rješenja jednadžbe
sinus	$\{x_{0} + 2 k π, π - x_{0} + 2 k π : k \in Z\}$ Specijalni slučajevi: $\{\frac{π}{2} + 2 k π : k \in Z\}$ ili $\{- \frac{π}{2} + 2 k π : k \in Z\}$
kosinus	$\{\pm x_{0} + 2 k π : x_{0} \neq 0, x_{0} \neq π, k \in Z\}$ Specijalni slučajevi: $\{2 k π : k \in Z\}$ ili $\{π + 2 k π : k \in Z\}$
tangens	$\{x_{0} + k π : k \in Z\}$
kotangens	$\{x_{0} + k π : k \in Z\}$

Na početku...

Ponovimo

- 1 , 1

R

Elementarne trigonometrijske jednadžbe

Trigonometrijske jednadžbe

Zadatak 1.

Primjer 1.

Kolekcija zadataka #1

Trigonometrijske jednadžbe oblika Asin(bx+c)+d=0 i Acos(bx+c)+d=0

Primjer 2.

Primjer 3.

Zadatak 2.

...i na kraju

$[- 1, 1]$

$R$