

Osim definicija trigonometrijskih funkcija na brojevnoj kružnici, naučili ste da je svaka trigonometrijska funkcija parna ili neparna.
U ovoj ćemo jedinici otkriti još jedno važno svojstvo trigonometrijskih funkcija.
Pogledajte sljedeće četiri sličice. Što je zanimljivo na svakoj od njih?
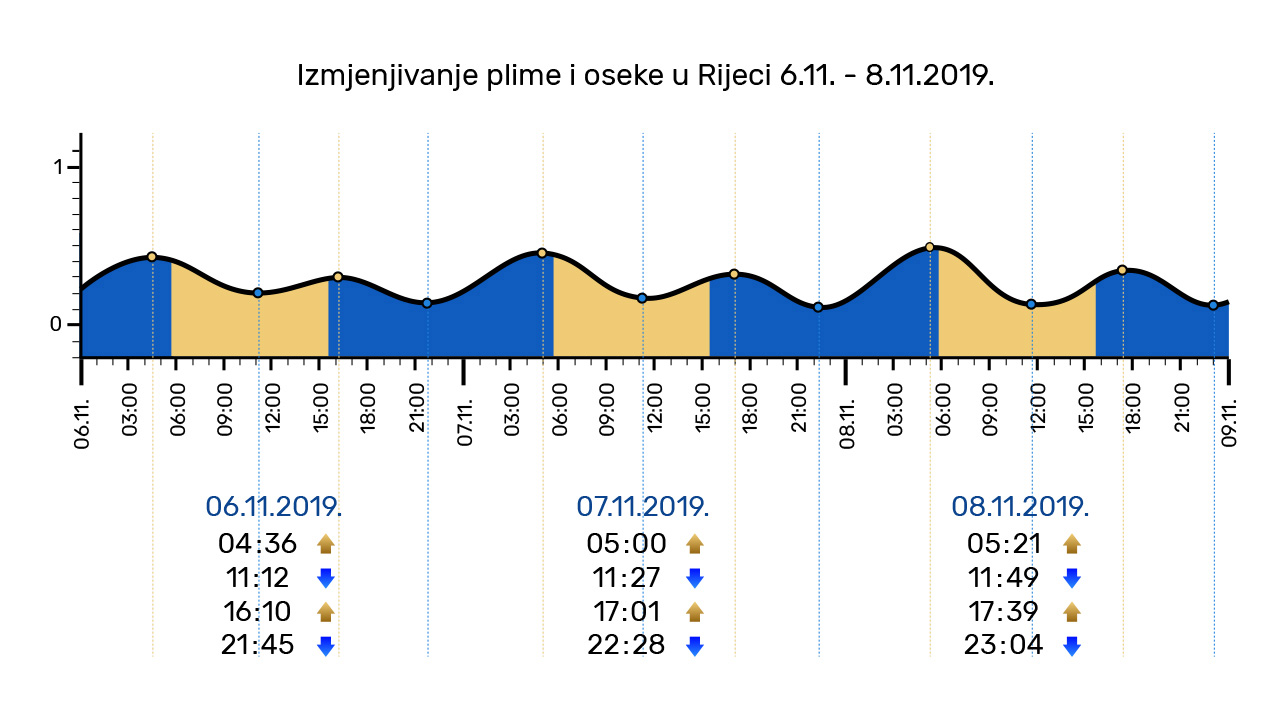
Posljednja slika prikazuje razinu mora (plimu i oseku) u Rijeci od 6. do 8. studenoga 2019. godine. Svjetliji dio označava vrijeme između izlaska i zalaska sunca.
Uočite u kojim se vremenskim intervalima izmjenjuju plima i oseka.
Za funkciju
kažemo da je periodična s periodom
ako vrijedi
Najmanji takav pozitivan broj
naziva se temeljni period.
Pomoću brojevne kružnice istražimo jesu li trigonometrijske funkcije periodične.
Poigrajte se sa sljedećom interakcijom. Pomičite točku po kružnici tako da pomičete klizač u lijevom prozoru. Pratite što se događa s njezinim koordinatama. Zamislite da putujete kružnicom.
Što predstavlja prijeđeni put po kružnici?
Razmislite!
Što se događa kada jedanput prođemo puni krug? Prolazimo li ponovno istim točkama? Što se mijenja? Pomoću prethodne interakcije odgovorite na sljedeća pitanja.
Analogno tome zaključite što vrijedi za kosinus broja
Vratite se na interaktivnu kružnicu. Neka je
Nakon kretanja u pozitivnom smjeru za
došli smo do iste točke, ali je vrijednost broja
Budući da smo glavnu mjeru kuta povezali s točkom na kružnici čije su koordinate vrijednosti sinusa i kosinusa, možemo zaključiti da se te vrijednosti ne mijenjaju ako argument uvećamo ili umanjimo za višekratnik broja
Trigonometrijske funkcije sinus i kosinus periodične su s temeljnim periodom Vrijedi:
Općenito, vrijedi
U sljedećoj animaciji pogledajte jesu li trigonometrijske funkcije tangens i kotangens periodične i ako jesu, koja im je glavna mjera kuta.
a. Trigonometrijska je funkcija tangens periodična, s temeljnim periodom:
b. Trigonometrijska je funkcija kotangens periodična, s temeljnim periodom:
Za trigonometrijske funkcije tangens i kotangens vrijedi:
Tangens i kotangens periodične su funkcije s temeljnim periodom
Pogledajte ponovno sliku plime i oseke s početka jedinice. Pokušajte utvrditi koliki je period plime i oseke, odnosno nakon koliko se sati izmjenjuju plima i oseka.
To ćete lako napraviti ako uočite/pročitate u koje se vrijeme pojavljuje oseka (najniža razina mora) ili plima (najviša razina mora). Koji period treba proći da bi se ponovila oseka ili plima?
Temeljni period trigonometrijskih funkcija
Upamtimo i ovo!
Neka su
Ako trigonometrijska funkcija sinus ili kosinus ima oblik ili njezin je temeljni period
Ako trigonometrijska funkcija tangens ili kotangens ima oblik ili njezin je temeljni perod .
Više o određivanju temeljnog perioda naučit ćete prilikom crtanja trgonometrijskih funkcija.