

Treći ste razred, približava se ispit zrelosti - matura. Koliko naučenog gradiva ste zaboravili?
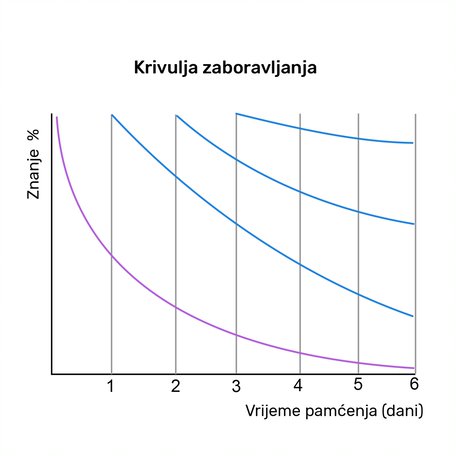
Poznata Ebbinghausova eksponencijalna krivulja zaboravljanja pokazuje da se naučeni materijal neposredno nakon učenja brže zaboravlja, a s vremenom sve sporije. Ponavljanjem gradiva, krivulja zaboravljanja je sve blaža, odnosno vrijeme učenja istog materijala je kraće, u odnosu na prethodno učenje.
Korelacija
Hermann Ebbinghaus je njemački psiholog (1850. - 1909.), utemeljitelj je eksperimentalnog proučavanja pamćenja. Otkrio je krivulju zaboravljanja i efekte razmaka učenja. Prvi je opisao i krivulju učenja. Zaslužan je i za otkrivanje optičke iluzije po njemu nazvane Ebbinghausova iluzija (na slici).
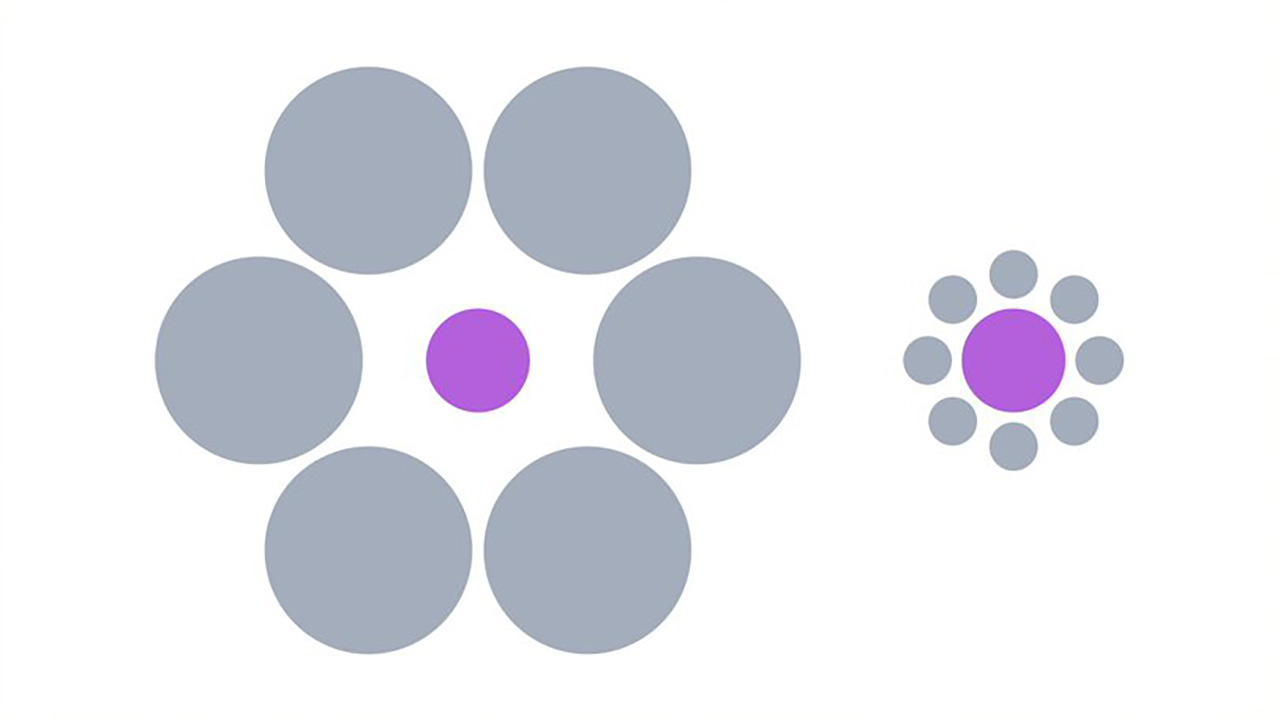
Ljubičasti krug na lijevoj strani se čini manji od onog na desnoj, a zapravo su identični.
Danas vam je na satu pažnja bila prilično loša. Činilo vam se da su svi pojmovi nebitni i u skladu s time ste i pratili nastavu. Vaša krivulja pamćenja dana je formulom
gdje je
vrijeme u minutama, a
količina zapamćenih podataka u postocima (uz pretpostavku da ste ipak sve čuli što se radilo na satu).
Pretpostavlja se da do
minute još uvijek sve znate. Dakle, funkcija je definirana za
Točke koje predstavljaju rješenje potražite u sljedećoj interakciji.
Prije nego što pomoću džepnog računala riješite zadatak, provjerite jeste li razumjeli zadatak.
Riješite prva tri zadatka. Izračunajte pomoću džepnoga računala vrijednosti funkcija za
i
sata.
Nakon
sata ostat će zapamćeno oko
gradiva.
Nakon
sati zaboravit ćete oko
gradiva.
Drugi dan u isto vrijeme znat ćete oko
gradiva.
Prije nego riješimo zadnji zadatak, ponovimo vezu između eksponencijalne i logaritamske funkcije.
Nakon što ste pažljivo pogledali animaciju, odgovorite na sljedeća pitanja.
Konačno, riješimo zadnji dio početnog zadatka.
Ako je
prikažite vrijeme
kao funkciju od
Riješite se nazivnika u jednakosti
i ostavite nepoznanicu na jednoj strani.
Primijenite pravilo koje povezuje potencije i korijene te na kraju pretvorite logaritamsku jednadžbu u eksponencijalni zapis (antilogaritmirajte).
Izračunajte nakon koliko minuta ćete zaboraviti
gradiva.
Možete koristiti prethodno dobivenu formulu, ali se i postepenim uvrštavanjem i računanjem može doći do rješenja.
minuta, što znači da da ćete pola gradiva zaboraviti za manje od jednog školskog sata.
Primjena eksponencijalne i logaritamske funkcije je raširena u svim područjima života, ali i granama znanosti. Pogledajmo još jedan primjer primjene.
je matematička konstanta (Eulerov broj, Napierova konstanta), iracionalan je broj,
Kada je
baza logaritamske funkcije pišemo
Ovakav logaritam nazivamo prirodni logaritam, a broj
zovemo baza prirodnog logaritma. O prirodnim logaritmima ćete nešto više naučiti kasnije.
Korelacija
Kako se penjemo u visine, atmosferski tlak eksponencijalno pada otprilike na svakih Tlak na razini mora (nadmorska visina ) je u prosjeku (ovisno o vremenskim uvjetima).
Neka je eksponencijalni pad dan formulom gdje je tlak na razini mora, konstanta, tlak u i visina u
Iz početnog podatka o tlaku na odredimo najprije konstanu
Izračunajte tlak na vrhu Mount Everesta, našeg najvišeg vrha Dinare i na vrhu Zagrebačke katedrale. Što primjećujete? Pronađite još neke zanimljive vrhove i odredite tlak na tim nadmorskim visinama.
Potrebne podatke potražite
na Internetu.