

Učenici često postavljaju pitanja:
"Odakle nam trigonometrijske vrijednosti u tablicama ili džepnim računalima?"
"Tko ih je izračunao i zašto?"
Vremeplov bi nam dobro došao za ovo istraživanje, jer putovanje počinje davno.
Naše bi istraživanje započelo oko 141 g. pr. Krista na otoku Rodosu. Posjetili bismo astronoma Hiparha.
On je izradio prve tablice povezane s trigonometrijom.
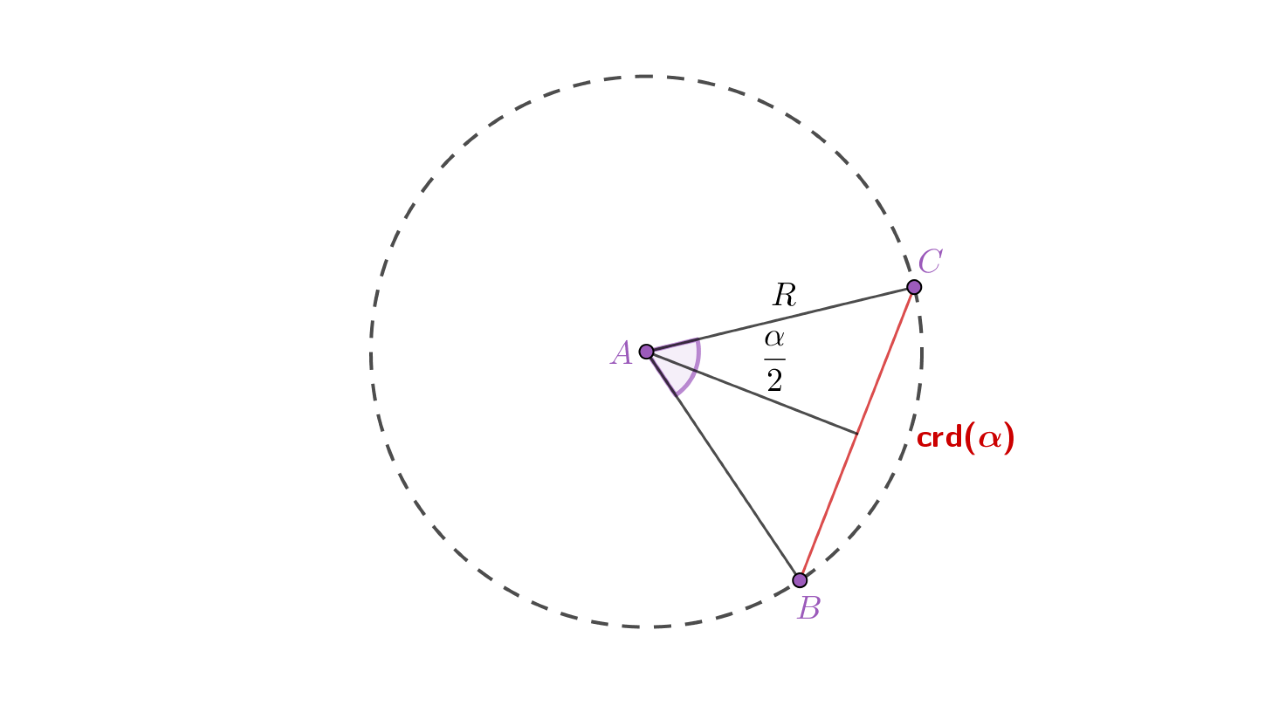
Duljina tetive obilježena je kao Hiparh i poslije Ptolomej dali su tablicu s popisom i za različite vrijednosti kuta koji se temeljio na određenoj vrijednosti radijusa. Povežimo sinus kuta i pomoću crteža.
pa je
Uz slijedi
Hiparhov rad nastavio je Ptolomej, koji je sastavio tablicu za određene kutove koje je izračunao pomoću Pitagorinog poučka, Hiparhove metode i Euklidove geometrije.
| Ptolemy's Table of Chords | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Ptolomejeve tablice daju vrijednost corda za središnje kutove u koracima od po
U tablici su vrijednosti središnjeg kuta (arc) u stupnjevima, „cord” (duljina tetive) i „sixtieths” - vrijednost koju treba dodati cordu za svaku dodatnu minutu kuta. Sixtieths je Ptolomej izračunao uzimajući razliku corda između susjednih lukova i dijeleći ih s
- koristeći se metodom linearne aproksimacije.
Geometrijski dokazi:
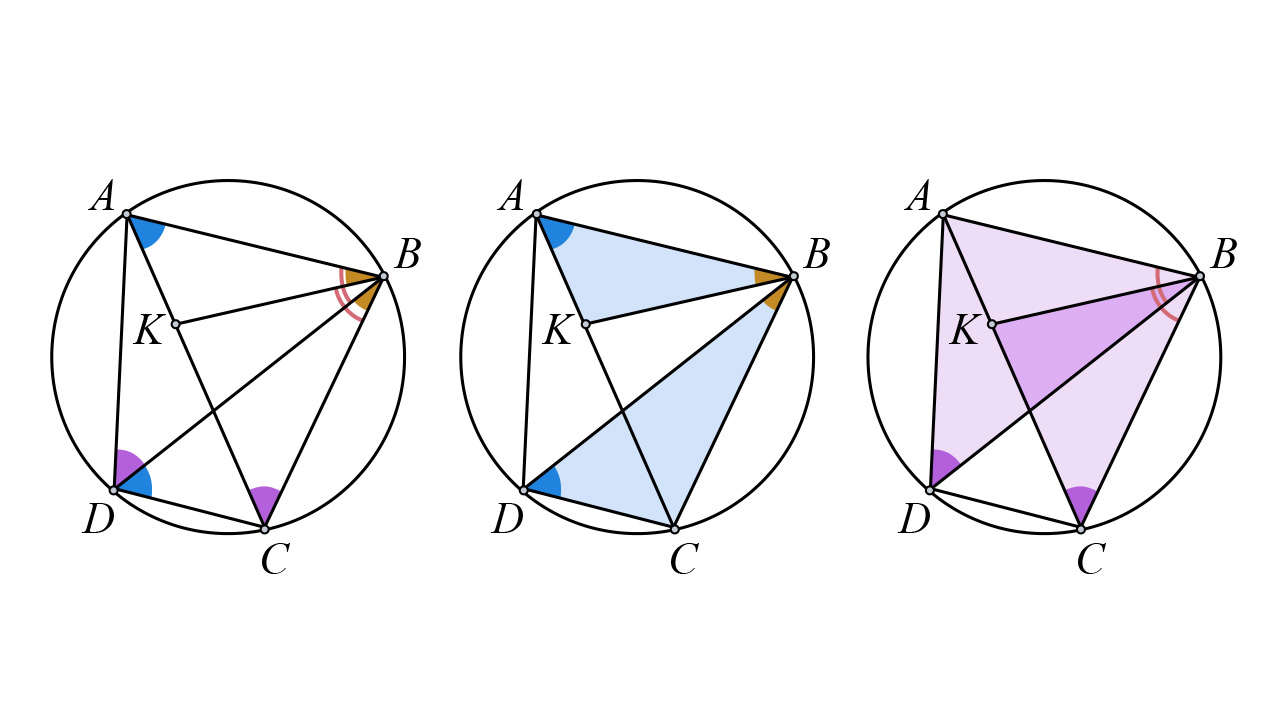
Ptolomej je iz svog poučka izveo tri zaključka, posljedice (Korolara) iz kojih je mogao izračunati cordove za više različitih kutova (ali nije dao formule):
Zaključci su ekvivalentni trigonometrijskim identitetima za sinus razlike, sinus polovičnog kuta i sinus zbroja.
Možemo li gdje su i realni brojevi, prikazati pomoću trigonometrijskih funkcija brojeva i
Prikažimo na brojevnoj kružnici točke i gdje su realni brojevi i iz intervala i
Duljina luka od točke do točke
Koordinate su naznačenih točaka sljedeće:
i
Na jednakost iz prethodnog zadatka primijenite formulu za udaljenost točaka zadanih svojim koordinatama.
Upotrijebite identitet
Što ste zaključili?
Postoji li veza između kosinusa razlike dvaju realnih brojeva i trigonometrijskih funkcija istih brojeva?
Izvedite formulu za kosinus zbroja. Umjesto
upotrijebite
te iskoristite parnost kosinusa i neparnost sinusa.
Pomoću formula za sinus i kosinus zbroja i razlike sinusa i kosinusa moguće je izvesti i formule za tangens i kotangens zbroja i razlike.
Adicijske formule za sinus i kosinus
Za svaka dva realna broja i vrijedi:
Adicijske formule za tangens i kotangens
Za svaka dva realna broja i njihov zbroj i razliku koji su u domeni funkcija tangens i/ili kotanges vrijedi:
Bez kalkulatora, pomoću adicijskih formula izračunajte sljedeće vrijednosti.
Pomoć:
Rastavite
na
Pomoć:
Kut od
rastavite na zbroj kuteva od
i
Pomoć:
Kut od
prikažite kao zbroj kuteva
i