Matematika 3 - 9.1 Jednadžba kružnice

Na početku...

Čarobnjak

Alisa igra igricu. Njezin lik treba uhvatiti i onesposobiti zlog čarobnjaka i njegove male pomoćnike. Alisa je u liku čarobnjaka čiji je domet $6$ metara. Budući da je na zaslonu svaki položaj definiran koordinatama, znamo da su Alisine koordinate $(5, 4) .$ Približila se malim zlim pomoćnicima čiji su položaji redom: Grin $(8, 7),$ Blu $(2, - 1)$ i Red $(9, 0) .$ Koje od tih pomoćnika Alisa može uhvatiti i onesposobiti?

Potrebno je pronaći udaljenost čarobnjaka od svakog pomoćnika i usporediti je s njegovim dometom. Prije nego što otkrijemo hoće li se Alisa približiti zlom čarobnjaku tako da uhvati njegove pomoćnike, prisjetimo se formule za udaljenost između dviju točkaka.

Ponovimo

Rasporedite dane udaljenosti na označena mjesta na slici.

|T_{1} T_{2}|

|x_{2} - x_{1}|

|y_{2} - y_{1}|

null

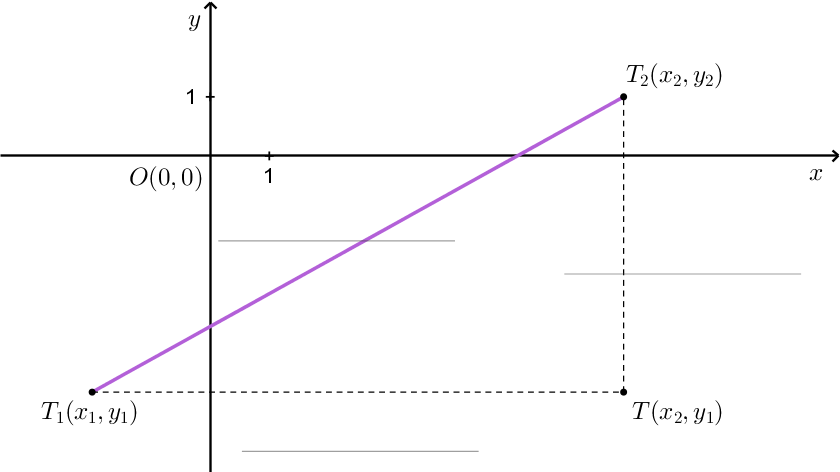
Promotrite sliku iz prethodnog zadatka i dopunite ispravno rečenice.

Točke $T, T_{1}, T_{2}$ čine

vrijedi

Izrazom

\sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}

računamo

između

točaka

T_{1}

T_{2} .

null

Prisjetimo se formule za udaljenost između proizvoljne točke $T_{1} (x_{1}, y_{1})$ od ishodišta koordinatnog sustava $O (0, 0) .$

Koja je formula za udaljenost točke $T_{1} (x_{1}, y_{1})$ od ishodišta koordinatnog sustava?

|O T_{1}| = |y_{1} - x_{1}|

|O T_{1}| = |x_{1} + y_{1}|

|O T_{1}| = {x_{1}}^{2} + {y_{1}}^{2}

|O T_{1}| = \sqrt{{x_{1}}^{2} + {y_{1}}^{2}}

null

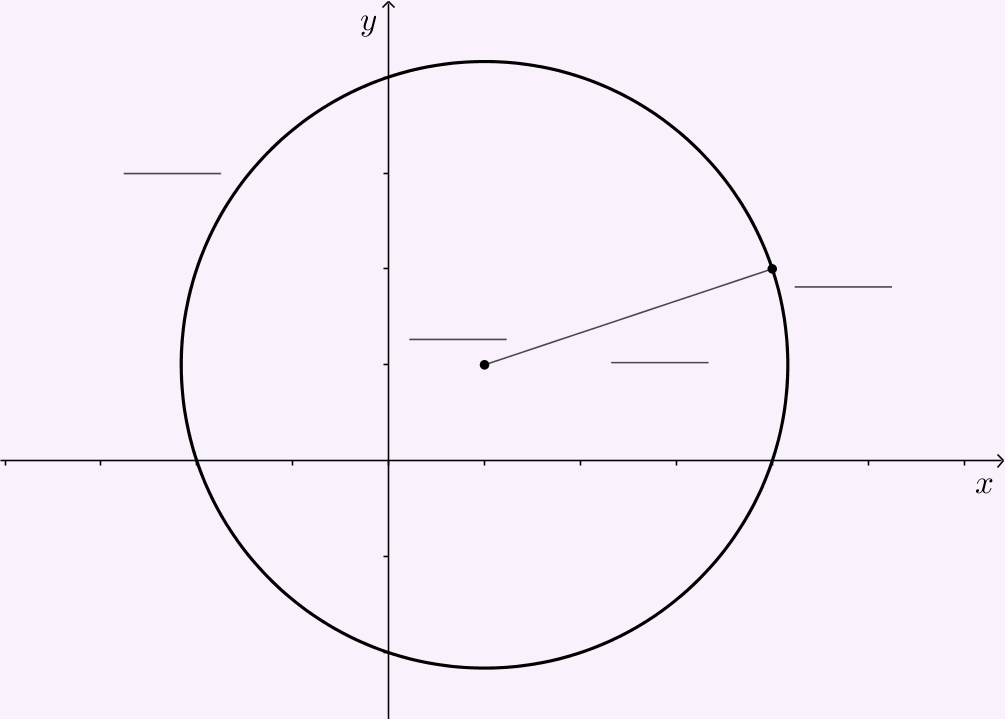
S kružnicom ste se u dosadašnjem školovanju susretali mnogo puta, od planimetrije do trigonometrije. Ponovimo definiciju kružnice koju znamo od prije.

Kružnica je skup

točaka

jednako

udaljenih

neke čvrste

točke

ravnine.

null

Kružnica u koordinatnom sustavu

Postavite oznake na pripadajuće mjesto na kružnici.

r

S (p, q)

T (x, y)

k (S, r)

null

Primjer 1.

Kružnica u koordinatnom sustavu dana je jednadžbom ${(x - 3)}^{2} + {(y + 1)}^{2} = 1 .$ Odredimo koordinate središta $S (p, q)$ i polumjer $r$ dane kružnice.

Generalizirajmo jednadžbu kružnice za proizvoljni polumjer $r$ i središte $S (p, q) .$

Pogledajte u sljedećem videoisječku kako iz dane jednadžbe kružnice možemo dobiti polumjer i središte te kako dobiti općenitu jednadžbu kružnice za proizvoljni polumjer $r$ i središte $S (p, q) .$

Jednadžba kružnice ${(x - p)}^{2} + {(y - q)}^{2} = r^{2}$ ima središte u $S (p, q)$ i polumjer $r .$

Kolekcija zadataka #1

Odredite koordinate središta i polumjer kružnice ${(x + 5)}^{2} + {(y + 6)}^{2} = 2 .$

$S (- 5, - 6), r = \sqrt{2}$

Odredite koordinate središta i polumjer kružnice ${(x - 2)}^{2} + y^{2} = 9 .$ Nacrtajte kružnicu u koordinatnom sustavu.

Grafički prikaz kružnice k(S(2,0), 3). — Grafički prikaz kružnice k(S(2,0), 3)

Odredite koordinate središta i polumjer kružnice $x^{2} + y^{2} = 5 .$ Nacrtajte kružnicu u koordinatnom sustavu.

Uočite da zadanu jednadžbu kružnice možemo zapisati u obliku

{(x - 0)}^{2} + {(y - 0)}^{2} = 5 .

Sada se lako vidi koje su koordinate središta.

Grafički prikaz kružnice sa središtem u ishodištu. — Grafički prikaz kružnice sa središtem u ishodištu

Određivanje jednadžbe kružnice

Odredimo jednadžbu kružnice sa središtem u ishodištu koordinatnog sustava i polumjerom $r .$

Kako je središte kružnice u ishodištu, koordinate središta su

S

koordinate ishodišta

polumjer

vrijedi

^{2}

^{2}

^{2}

Pomoć:

Napišite koordinate središta kao uređeni par sa zagradama, bez razmaka.

null

Jednadžba kružnice sa središtem u ishodištu koordinatnog sustava i polumjerom $r .$

$x^{2} + y^{2} = r^{2}$

Primjer 2.

Za dane koordinate središta $S (- 2, 2)$ nacrtajmo kružnicu koja prolazi ishodištem koordinatnog sustava te joj odredimo jednadžbu.

Nacrtajmo kružnicu sa zadanim središtem koja prolazi ishodištem.

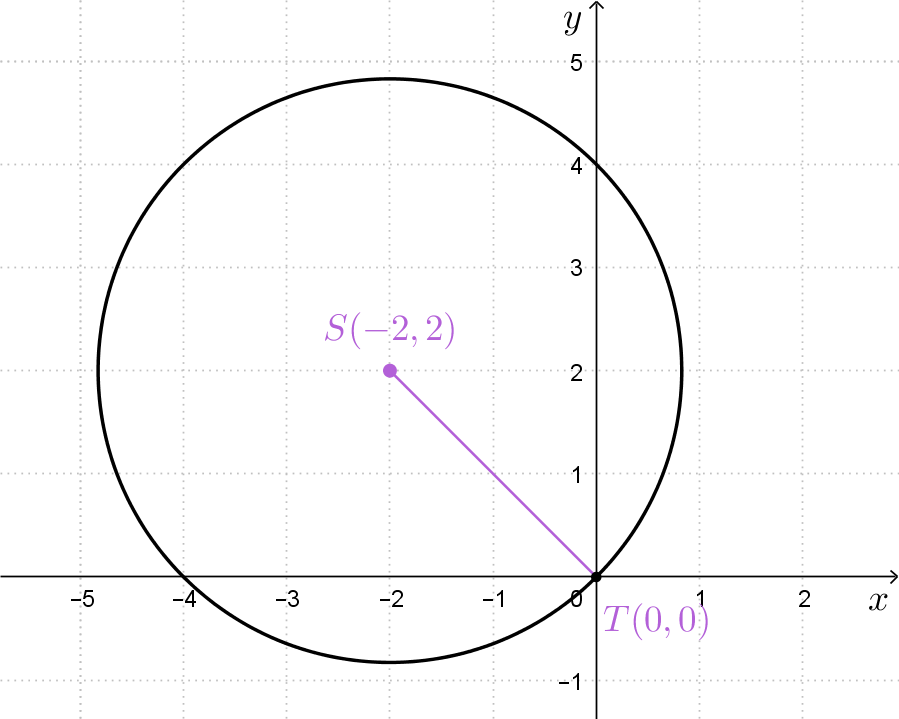
Grafički prikaz kružnice sa središtem u S(-2,2). — Grafički prikaz kružnice sa središtem u S(-2,2)

Kako odrediti polumjer? S obzirom na to da je udaljenost između središta i točke na kružnici jednaka polumjeru, koristit ćemo se formulom za udaljenost između dviju točaka, odnosno jednadžbom kružnice tako da:

umjesto $x$ i $y$ uvrstimo koordinate dane točke $T$ na kružnici.

${(x - p)}^{2} + {(y - q)}^{2} = r^{2} \Rightarrow r^{2} = {(0 - (- 2))}^{2} + {(0 - 2)}^{2} = 4 + 4 = 8$

Sada, kada znamo da je $r = 2 \sqrt{2},$ možemo napisati jednadžbu kružnice.

${(x + 2)}^{2} + {(y - 2)}^{2} = 8$

Kružnicu možemo, osim središtem i točkom na kružnici, odrediti i s pomoću triju točkaka. Uvrstimo u jednadžbu kružnice koordinate zadanih točaka i sustavom triju jednadžbi s trima nepoznanicama dobijemo koordinate središta i polumjer.

Kružnicu možemo zadati i uz neke druge uvjete na središte ili polumjer.

Zadatak 1.

Ako točka $T (1, 1)$ pripada kružnici, a središte leži na sjecištu pravca $y = - x + 4$ s osi apscisa, odredite jednadžbu kružnice.

${(x - 4)}^{2} + y^{2} = 10$

Prije nego što riješite zadatak pokušajte nacrtati uvjete zadatka i rješenje odrediti iz grafa. U nastavku je interakcija koja vam može pomoći pri određivanju kružnice.

Polje za unos rabimo za upisivanje koordinata točke ili za jednadžbu pravca.
Naredbu Točka na objektu rabimo za postavljanje točke, npr. na pravac, kružnicu ili neki drugi objekt koji imamo.
Za crtanje kružnice možemo upotrijebiti više naredbi (ovisno što nam je zadano) ‒ isprobajte!

Zapamtite: sve što možemo konstruirati možemo i analitički izračunati, i obrnuto.

Sljedeće zadatke riješite analitički, a zatim pomoću prethodne interakcije provjerite svoja rješenja.

Kolekcija zadataka #2

Kvadratu $A B C D,$ kojem je zadana dijagonala $\bar{A C},$ $A (- 1, - 2) i C (3, 4)$ opišite i upišite kružnicu. Koje su jednadžbe dobivenih kružnica?

${(x - 1)}^{2} + {(y - 1)}^{2} = \frac{13}{2}$ i
${(x - 1)}^{2} + {(y - 1)}^{2} = 13$

Kružnica se nalazi između usporednih pravaca $x = - 1 i x = 5 .$ Ako je središte na pravcu $y = x - 5,$ odredite jednadžbu kružnice.

${(x - 2)}^{2} + {(y + 3)}^{2} = 9$

Odredite jednadžbu kružnice zadanu trima točkama $A (- 2, 0), B (3, - 5) i C (0, 4) .$

Uvrstimo sve tri točke u jednadžbu kružnice i riješimo sustav.

{(- 2 - p)}^{2} + q^{2} = r^{2}

{(3 - p)}^{2} + {(- 5 - q)}^{2} = r^{2}

\underline{p^{2} + {(4 - q)}^{2} = r^{2}}

{(x - 3)}^{2} + y^{2} = 25

...i na kraju

Jeste li uspjeli odgovoriti na pitanje iz uvoda? Koliko se Alisa uspjela približiti zlom čarobnjaku? Nacrtajte koordinate njihovih položaja. Što znači da je domet

6 ?

Napišite jednadžbu kružnice u čijem je središtu Alisa kao čarobnjak te nacrtajte njezin domet djelovanja. Nacrtajte i mjesta gdje su mali zli čuvari čarobnjaka kojeg treba istjerati iz Zemlje.

Grafičko rješenje uvodnog problema, Alisin domet. — Grafički prikaz Alisinog dometa djelovanja

Može li Alisa u ulozi čarobnjaka spasitelja onesposobiti sva tri pomoćnika?

null

Koji je najdalje, ali još u krugu od $6$ metara, i prvog bi ga trebalo onesposobiti?

Blu

Grin

Red

null