

Broj je decimalan pa nije ni prirodni ni cijeli. Ima beskonačni decimalni prikaz, ali znamenke se pojavljuju nasumično, nema skupine znamenki koja se periodično ponavlja. Racionalni brojevi s beskonačnim decimalnim zapisima su periodični. Zato taj broj nije racionalan. Vidimo da postoje brojevi koji nisu racionalni. Nazivamo ih iracionalni brojevi.
Broj je iracionalan ako ima beskonačan neperiodični decimalni zapis.
Odgovorite na pitanja o decimalnom zapisu iracionalnoga broja.
Ako je broj iracionalan, njegov je decimalni zapis beskonačan.
Ako je broj iracionalan, u njegovu decimalnom zapisu nema skupine znamenki koja se periodično ponavlja.
Ako je broj iracionalan, u njegovu decimalnom zapisu nema pravilnosti.
Je li broj iracionalan? Iza decimalne točke nižu se prirodni brojevi, a između dvaju susjednih prirodnih brojeva je 0.
Da. Ne postoji period koji se ponavlja.
Iracionalni broj ne može se zapisati u obliku razlomka
Ako se broj može zapisati u obliku razlomka onda je taj broj racionalan. Racionalni brojevi imaju ili konačne ili beskonačne periodične decimalne zapise.
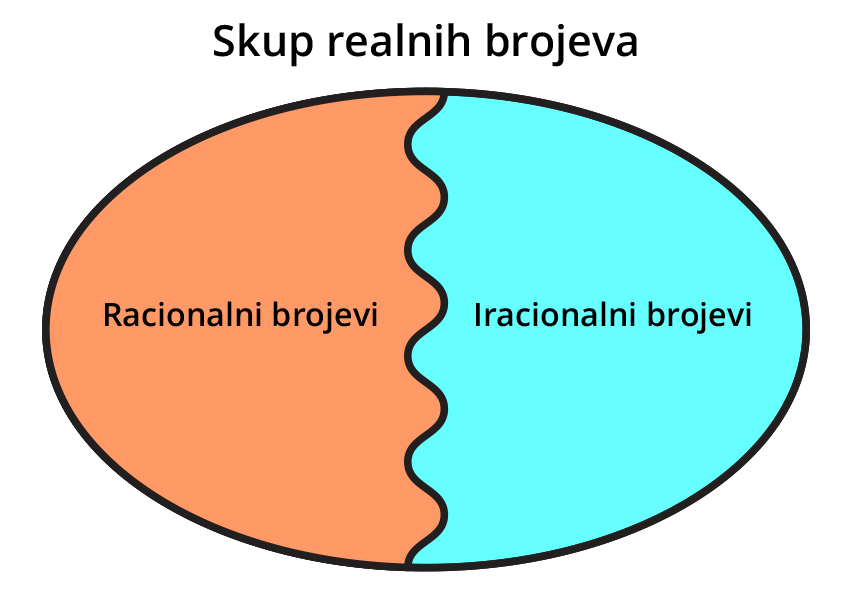
Realni broj je onaj koji je racionalan ili iracionalan. Skup realnih brojeva označavamo s
U kakvu su odnosu skupovi realnih, racionalnih i iracionalnih brojeva? Dopunite.
Racionalne brojeve možemo zapisati u razlomačkom ili u decimalnom zapisu. Oba su zapisa jednostavna, čak i ako je riječ o beskonačnom zapisu jer je on periodičan pa je dovoljno zapisati period. Kako zapisati iracionalni broj? Kako računati s iracionalnim brojevima?
Iracionalni brojevi imaju beskonačne neperiodične zapise. Zato pri zapisivanju i računanju s iracionalnim brojevima upotrebljavamo posebne oznake za neke od njih, zapisujemo ih s pomoću nekih matematičkih radnji ili zamjenjujemo približnim vrijednostima. Približna vrijednost iracionalnog broja je broj s konačnim decimalnim zapisom koji se u cjelobrojnom i decimalnom dijelu podudara s cjelobrojnim dijelom i početnim decimalama iracionalnoga broja.

Poznajete li posebnu oznaku za neki iracionalni broj?
Posebnom se oznakom zapisuje broj
Jednu grupu iracionalnih brojeva čine oni koji se mogu zapisati s pomoću korijena. Takav je, na primjer, broj Iracionalnost broja uočili su Pitagorejci. U videu pogledajte dokaz iracionalnosti broja
Dokažite da je iracionalan.
Pretpostavimo da je
racionalan. To znači da postoje prirodni brojevi
i
za koje vrijedi da je
Odaberimo brojeve
i
tako da je razlomak
potpuno skraćen. Kvadriranjem dobivamo
iz čega zaključujemo da je broj djeljiv s Ako je djeljiv s onda je i djeljiv s pa zapisujemo
Uvrštavanjem dobivamo
Ponovno možemo zaključiti da je broj
djeljiv s
Ako je
djeljiv s
onda je i
djeljiv s
Zaključili smo da su
i
djeljivi s
što znači da razlomak
nije skraćen do kraja. To je nemoguće jer razlomak uvijek možemo skratiti do kraja.
Pogrešna je početna pretpostavka da je racionalan pa zaključujemo da je iracionalan.
Je li broj iracionalan? Zašto? Pokušajte dokazati da je iracionalan na isti način kao u prethodnom zadatku. Koji od zaključaka ne vrijedi?
Broj jednak je pa je racionalan. Uz oznake kao u prethodnom zadatku, iz činjenice da je broj djeljiv s ne možemo zaključiti da je i djeljiv s Na primjer, je djeljiv s , ali nije.
Za koje je prirodne brojeve broj iracionalan? Dopunite.
Skup racionalnih brojeva zatvoren je s obzirom na zbrajanje i množenje. Što možemo reći o zbroju i umnošku dvaju iracionalnih brojeva? A o zbroju i umnošku racionalnoga i iracionalnoga broja?
Zbroj racionalnog i iracionalnog broja je:
Zbroj dvaju iracionalnih brojeva je:
Umnožak iracionalnih brojeva je:
Umnožak racionalnog broja različitog od 0 i iracionalnog broja je:
Dokažite tvrdnje iz prethodnog zadatka.
Dovucite zadane elemente na pravo mjesto.
Prikažite zadani racionalni broj na brojevnom pravcu.
Iracionalne brojeve možemo prikazati tako da odredimo približnu vrijednost iracionalnoga broja. Na primjer
Prikažite približno zadane iracionalne brojeve na brojevnom pravcu.
Primjer 1.
Neke iracionalne brojeve možemo prikazati precizno. Pogledajte animaciju koja prikazuje prikaz broja na brojevnom pravcu.
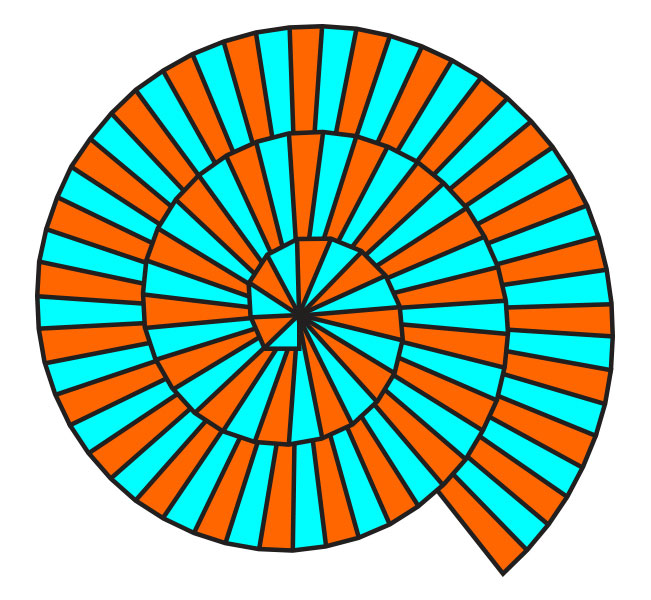
Grčki matematičar Theodorus pokazao je kako konstruirati dužinu duljine Jeste li čuli za spiralu drugog korijena? Na papiru napravite konstrukciju s jednakokračnim pravokutnim trokutom čije su katete duljine Hipotenuza tog trokuta, duljine kateta je idućega pravokutnog trokuta. Druga je kateta duljine pa će hipotenuza drugog trokuta biti duljine Postupak nastavite. Ukrasite svoju spiralu.
U matematici se tvrdnje dokazuju. Katkad postoji više načina kako dokazati neku tvrdnju. Znate li neku tvrdnju koju možete dokazati na različite načine? U ovoj smo jedinici dokazali iracionalnost broja Jeste li se susreli s drukčijim dokazom?
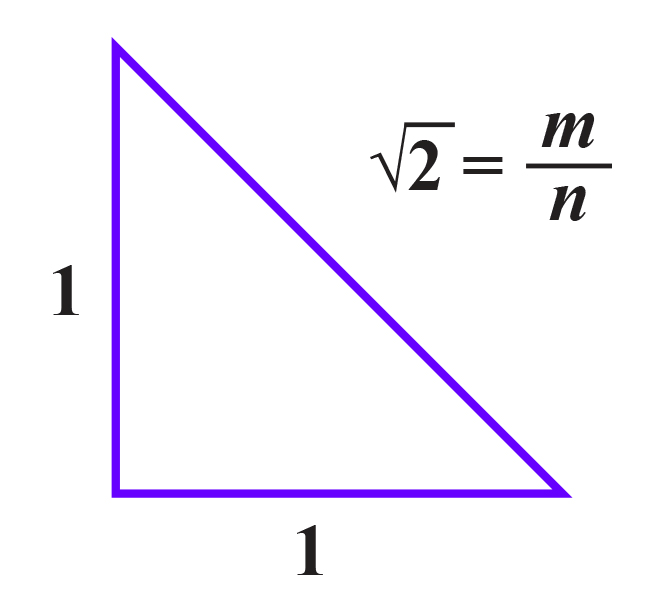
Postoji više dokaza iracionalnosti broja Jedan je od njih geometrijski. Promotrimo jednakokračni pravokutni trokut na slici. Duljine su kateta pa je duljina hipotenuze Pretpostavimo da je racionalan. Tada ga možemo zapisati u obliku
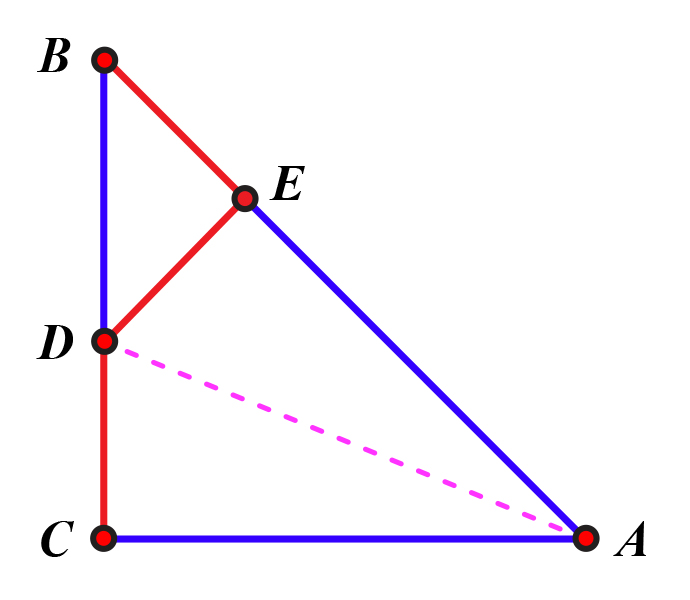
Promotrimo trokut čije su duljine stranica Taj je trokut sličan polaznom (zašto?), a duljine su stranica prirodni brojevi. Točka je sjecište simetrale kuta i stranice Točka je nožište okomice iz točke na stranicu
Uočite slične trokute na slici. Dokažite sličnost. Dokažite da su duljine stranica trokuta
prirodni brojevi.
Trokut
jednakokračan je pravokutni trokut čije su duljine stranica prirodni brojevi manji od duljina stranica trokuta
Primijenimo isti postupak na trokut
Što vrijedi za novi trokut koji tako nastaje? Nastavimo ponavljati postupak. Objasnite u čemu je proturječnost.
Slični su trokuti
i
jer imaju jednake kutove. Trokut
jednakokračan je pa zaključujemo da je i trokut
jednakokračan.
Označimo
Točka
je na simetrali kuta
pa je jednako udaljena od krakova
i
Zaključujemo:
Trokut
jednakokračan je pa je i
Označili smo
Tada je i
Vrijedi:
pa je
prirodni broj.
Također je prirodni broj pa su duljine stranica trokuta prirodni brojevi manji od duljina odgovarajućih stranica trokuta
Primijenimo li isti postupak na trokut
dobit ćemo novi trokut čije su duljine stranica prirodni brojevi. Nastavimo li ponavljati postupak, svaki će idući trokut imati stranice čije su duljine manje od duljina odgovarajućih stranica iz prethodnog koraka, ali će sve duljine biti prirodni brojevi. To je nemoguće jer postoji najmanji prirodni broj.
U ovoj ste jedinici mogli naučiti što su iracionalni i realni brojevi te kako se realni brojevi prikazuju na brojevnom pravcu. U idućim zadatcima provjerite svoje znanje.
Presjek skupova racionalnih i iracionalnih brojeva je prazan.
Svaki je realni broj iracionalan.
Svi iracionalni brojevi elementi su skupa { nije potpun kvadrat}.
Svakoj točki na brojevnom pravcu odgovara jedan realni broj.
Svaki je korijen iz prirodnog broja iracionalan.
Broj s beskonačnim decimalnim zapisom je iracionalan.
Broj prikazan u obliku razlomka nije iracionalan.
Cijeli brojevi nisu realni.
Uparite elemente.
|
|
Racionalan broj |
|
|
Iracionalan broj |
Poredajte skupove tako da je prethodni podskup sljedećeg.