


Dvojica su ribara pri povratku iz večernjeg ribolova ostala bez goriva. Kako njihov čamac nije imao mjerne instrumente, trebalo je nekako odrediti koliko su udaljeni od obale. S obzirom na to da su bili u dometu svjetla sa svjetionika, uz malo računanja to im nije bilo osobito teško. Znali su da je vrh svjetionika na nadmorskoj visini od oko metara, a u trenutku kada se ribar visine uspravio, procijenili su da je njegova sjena duljine metara. Kako su odredili udaljenost čamca od obale i koliko ona iznosi?
Pogledajmo sljedeću skicu.

Treba odrediti u kojoj su vezi poznate duljine
i nepoznata duljina
Prvo ćemo općenito istražiti vezu između dužina koje odsijecaju paralelni pravci na krakovima nekog kuta, a onda ćemo izračunati duljinu dužine
Neka su paralelni pravci koji sijeku krakove kuta Točke redom su presjeci tih pravaca s krakom a točke redom njihovi presjeci s krakom
U sljedećoj interakciji pomičite točke na krakovima kuta i promatrajte označene omjere.
Što ste uočili?
Odaberite sljedeće elemente tako da dobijete istinitu jednakost.
Ako krakove nekog kuta presiječemo s dva paralelna pravca, onda su dužine koje ti pravci odsijecaju na jednom kraku proporcionalne dužinama koje ti pravci odsijecaju na drugom kraku. Ovu tvrdnju nazivamo Talesov poučak.
Pišemo

Tales (625. - 548. pr. Kr.) bio je grčki znanstvenik, matematičar i državnik iz Mileta u maloj Aziji. Smatrali su ga jednim od sedam grčkih mudraca.
Tales je prvi predvidio pomrčinu Sunca 585. g. pr. Kr.
Izmjerio je visinu Keopsove piramide koristeći sunčeve zrake i proporcionalnost dužina. Izabrao je sunčani dan i trenutak kada je sjena štapa koji je zabio u pijesak pokraj piramide jednaka visini samog štapa. To je onda primijenio i na piramidu i izmjerivši njezinu sjenu zapravo izmjerio i njezinu visinu.
U matematici je dao nekoliko važnih poučaka kao što je ovaj, ali je još važnije što je Tales bio prvi koji je naglasio da nije dovoljno samo opažati pojave nego ih treba i dokazati.
Koristeći se Talesovim poučkom, dokažite sljedeće razmjere kao posljedicu Talesova poučka:
Odsječci paralelnih pravaca između krakova kuta proporcionalni su odsječcima na jednom kraku.
Pišemo
Primijenite Talesov poučak na uvodni primjer.
Kako su pravci
paralelni, prema Talesovu poučku vrijedi da je
Tada je
metara.
Na slici je trokut u kojem je povučena paralela s jednom stranicom. Koji su od sljedećih razmjera točni?
Ako su pravci paralelni, odredite nepoznate duljine označene na sljedećim slikama.

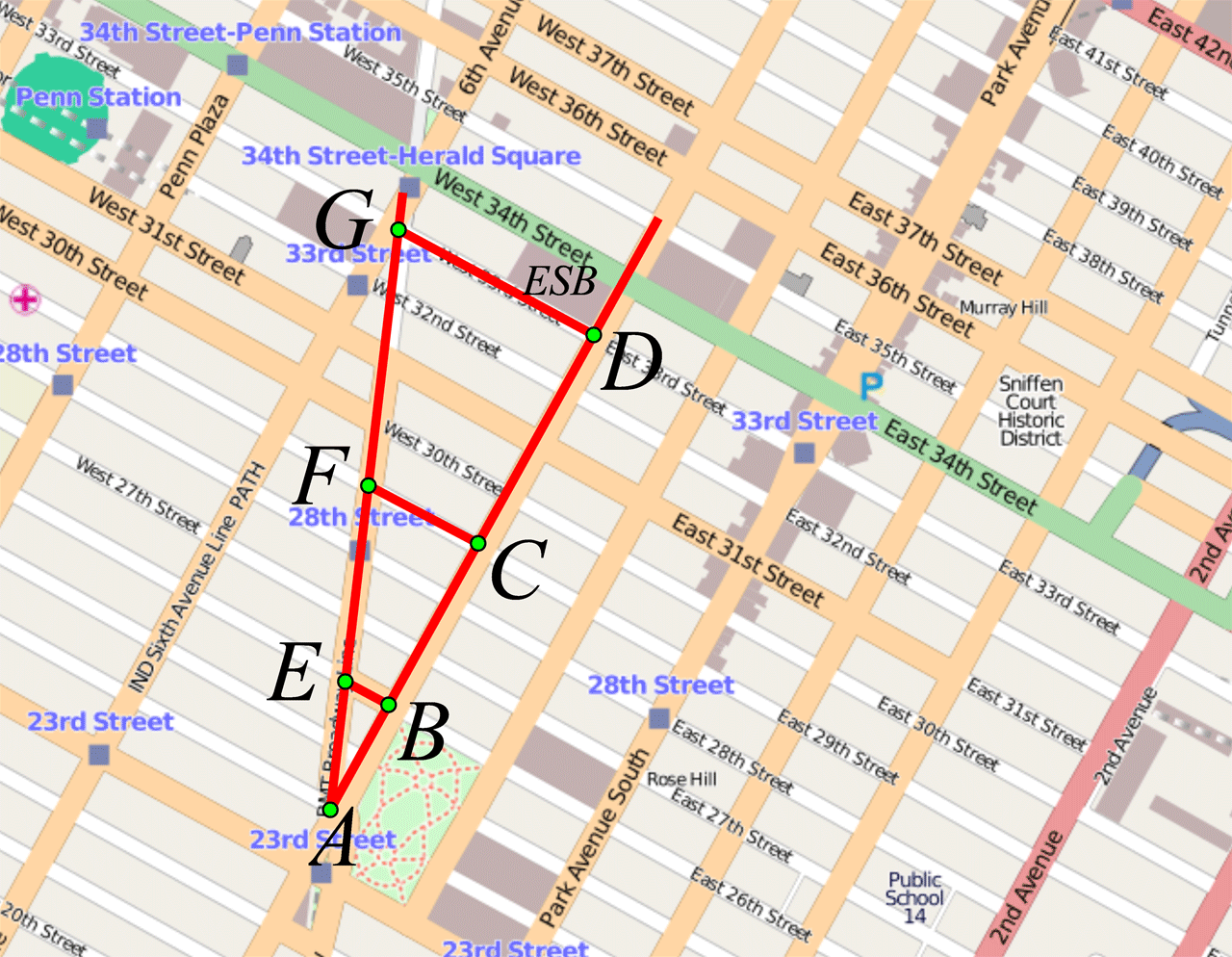
U New Yorku je veći dio grada ispresijecan paralelenim ulicama.
Mia je krenula Petom avenijom prema Muzeju matematike (
) i Empire State Buildingu (
). Brojila je korake. Od početne točke (
) do Muzeja ima
koraka. Od Muzeja do 29. ulice oko
koraka, a odatle do 33. ulice (
) u kojoj je
koraka. Zanimalo ju je koliko bi koraka napravila na istim dionicama puta da je išla Šestom avenijom. Kako je njezin hotel u 29. ulici, zna da je duljina te ulice, između Pete i Šeste avenije, oko
koraka.
Pretpostavit ćemo da su Mijini koraci približno iste duljine i da su paralelne ulice okomite na Petu aveniju (pravac
).
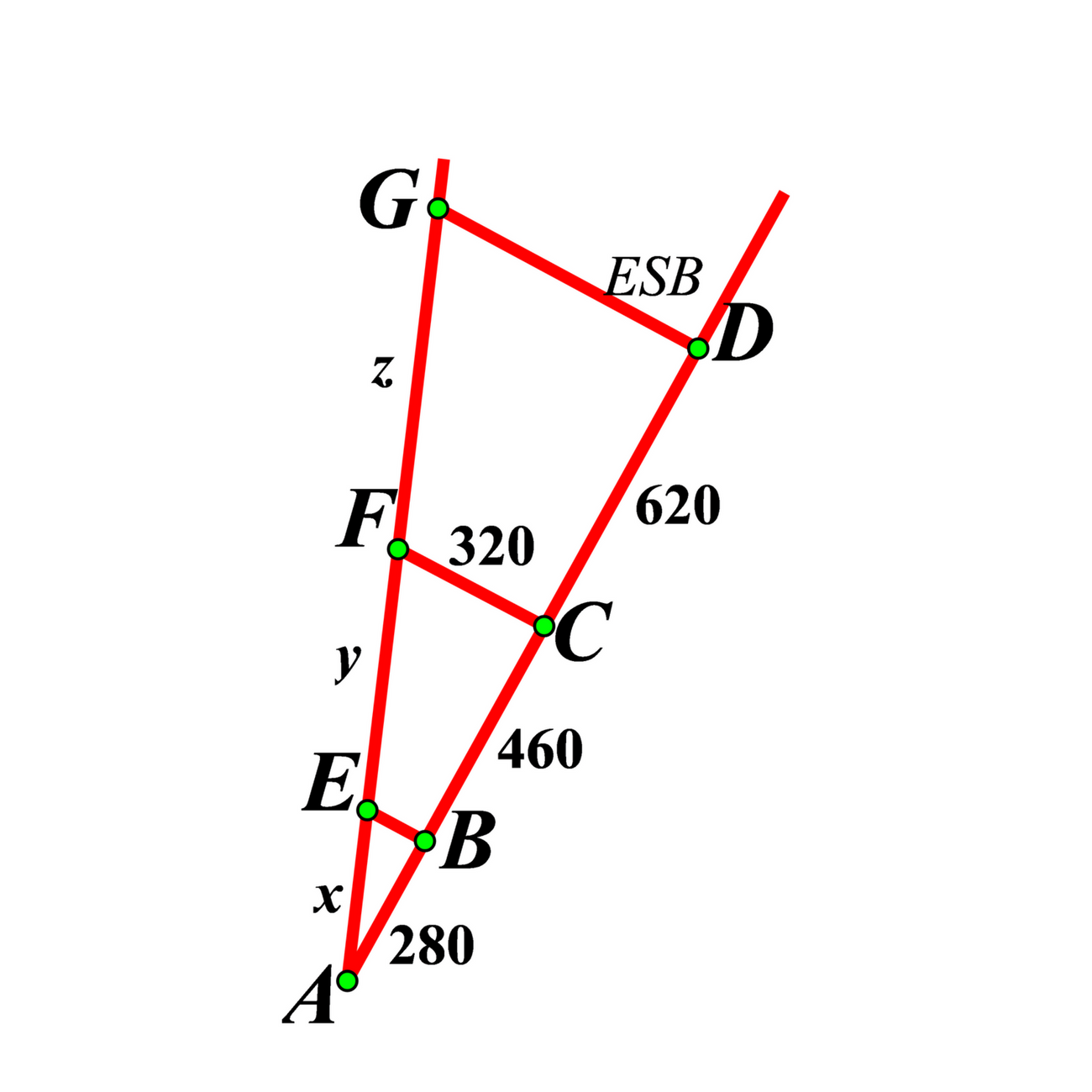
Primijenimo prvo Pitagorin poučak na trokut
Primijenimo sada Talesov poučak o proporcionalnim dužinama:
Primjer 1.
Jesu li grede na krovu prikazane kuće paralelne?
Kako biste to provjerili ako imate na raspolaganju samo metar za mjerenje duljine?

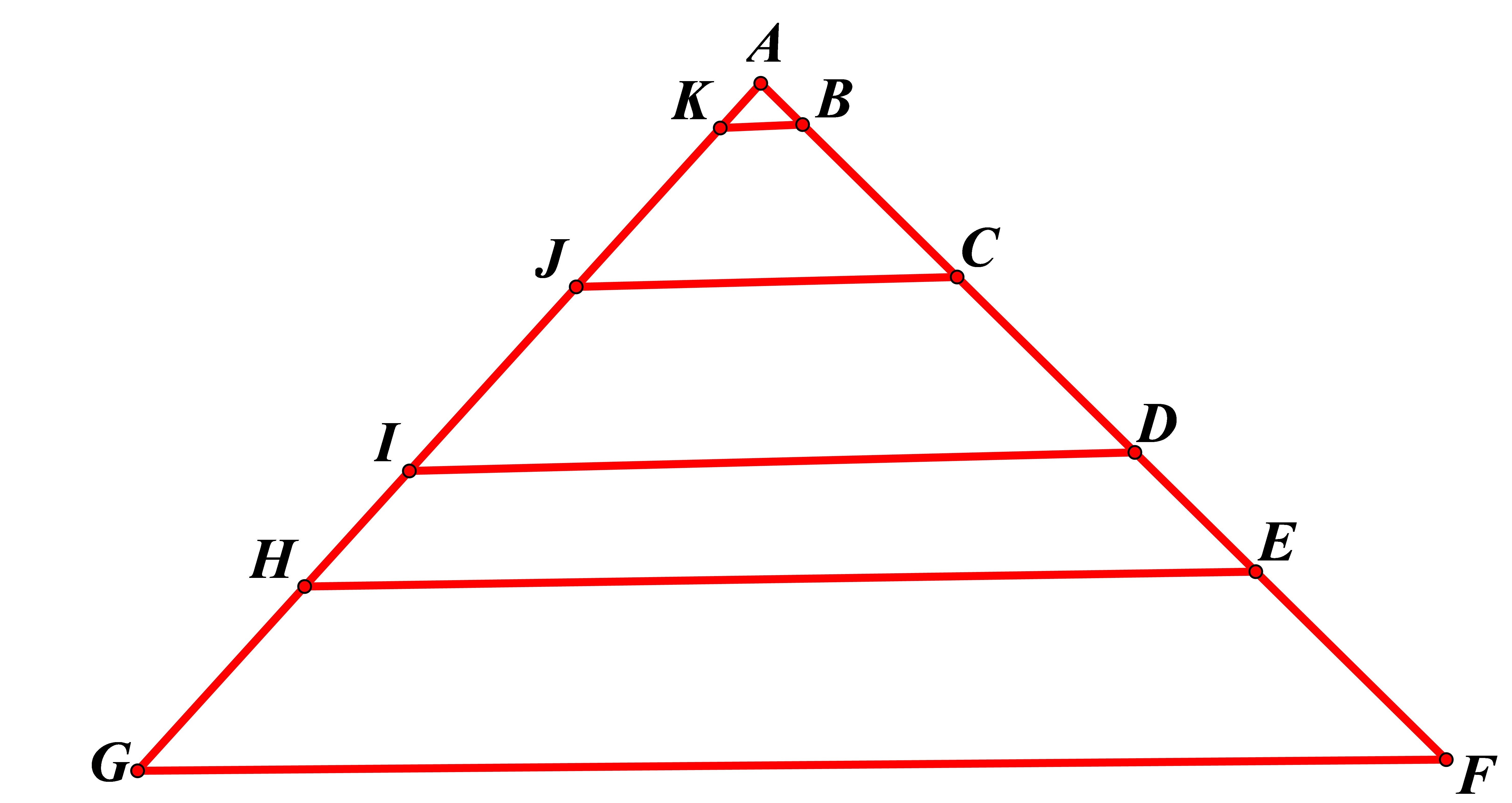
Mogu se izmjeriti dužine koje promatrani pravci
odsijecaju na krakovima kuta
i vidjeti jesu li proporcionalne. Ako jesu, tada su i promatrani pravci paralelni.
To možemo zaključiti jer vrijedi sljedeća tvrdnja.
Ako dva pravca odsijecaju na krakovima kuta proporcionalne dužine, onda su ti pravci paralelni. Ovu tvrdnju nazivamo Obrat Talesova poučka o proporcionalnosti.
Dokaz.
Neka pravci
odsijecaju na krakovima
proporcionalne dužine, odnosno vrijedi
Točke
redom su presjeci tih pravaca s krakom
a točke
redom njihovi presjeci s krakom
Pretpostavimo da pravci
nisu paralelni. Neka je pravac
takav da je
paralelan s pravcem
i prolazi točkom
Neka je
točka u kojoj pravac
siječe krak
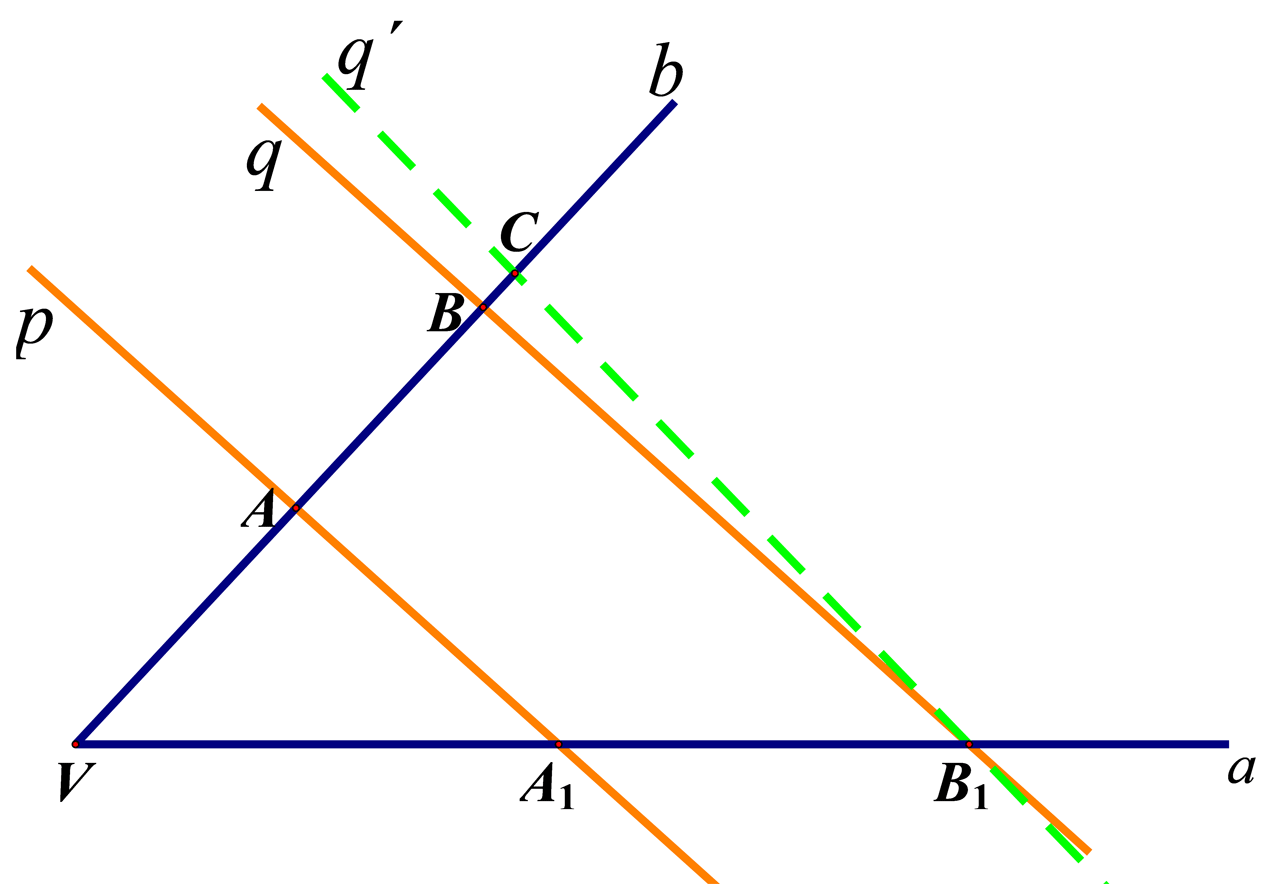
Kako su pravci
i
paralelni i sijeku krakove kuta
prema Talesovu poučku oni odsijecaju proporcionalne dužine na krakovima tog kuta. Stoga vrijedi
Usporedimo li ovaj razmjer s početnim uvjetom
zaključujemo da je
Ovo je moguće jedino ako se točke
podudaraju, no tada se i pravci
podudaraju, što je suprotno našoj pretpostavci. Zaključujemo da su pravci
paralelni.
U sljedeća tri zadatka provjerite jesu li pravci na slici paralelni.
Pridružite dužinama
trokuta
duljine tako da pravci
budu paralelni.
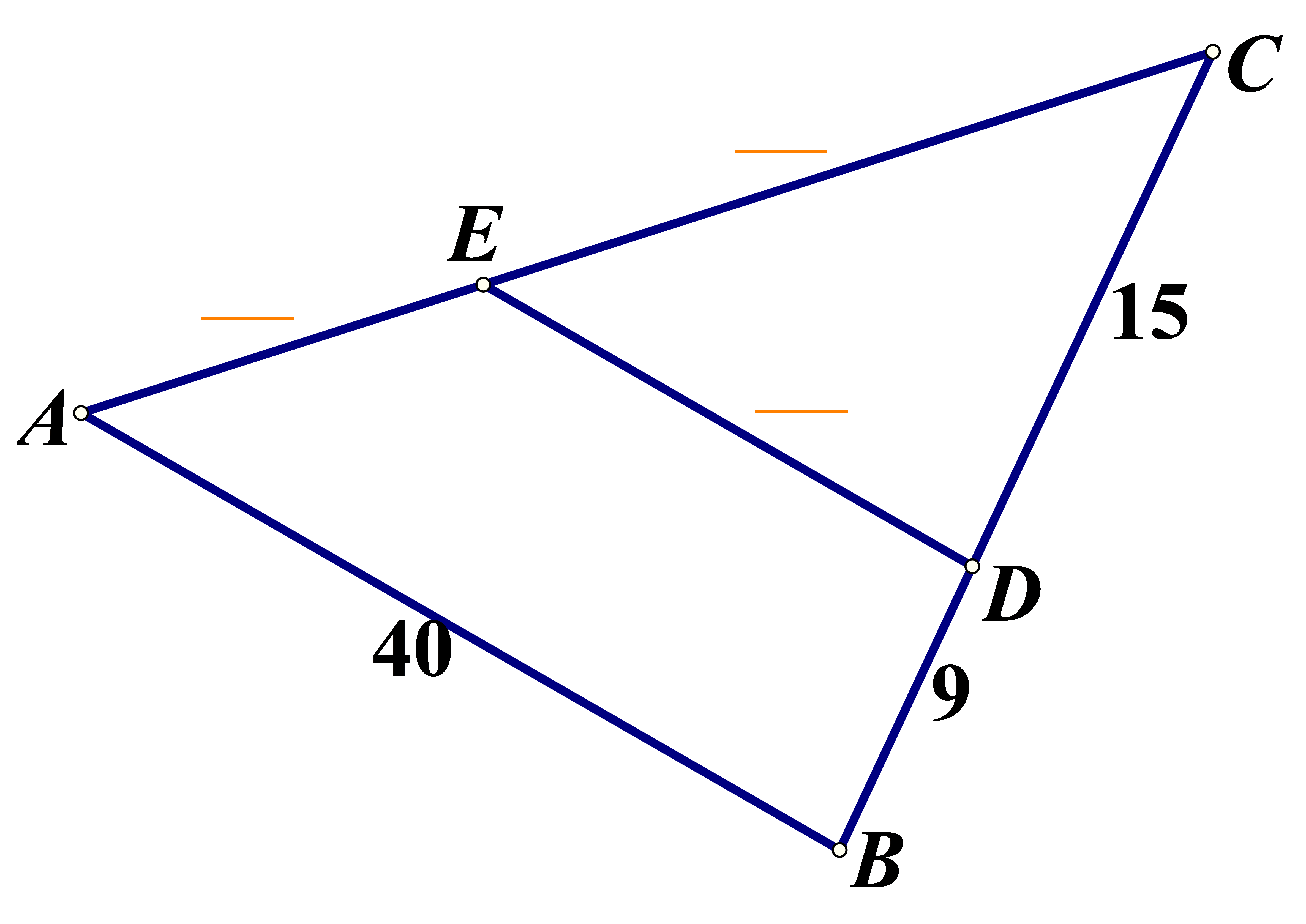
12
20
25
Duljine stranica trokuta
jesu
Povucite simetralu kuta pri vrhu
i označite s
sjecište simetrale i nasuprotne stranice. Možete li izračunati duljine dužina
Je li točka
polovište stranice
U kojem omjeru točka dijeli stranicu
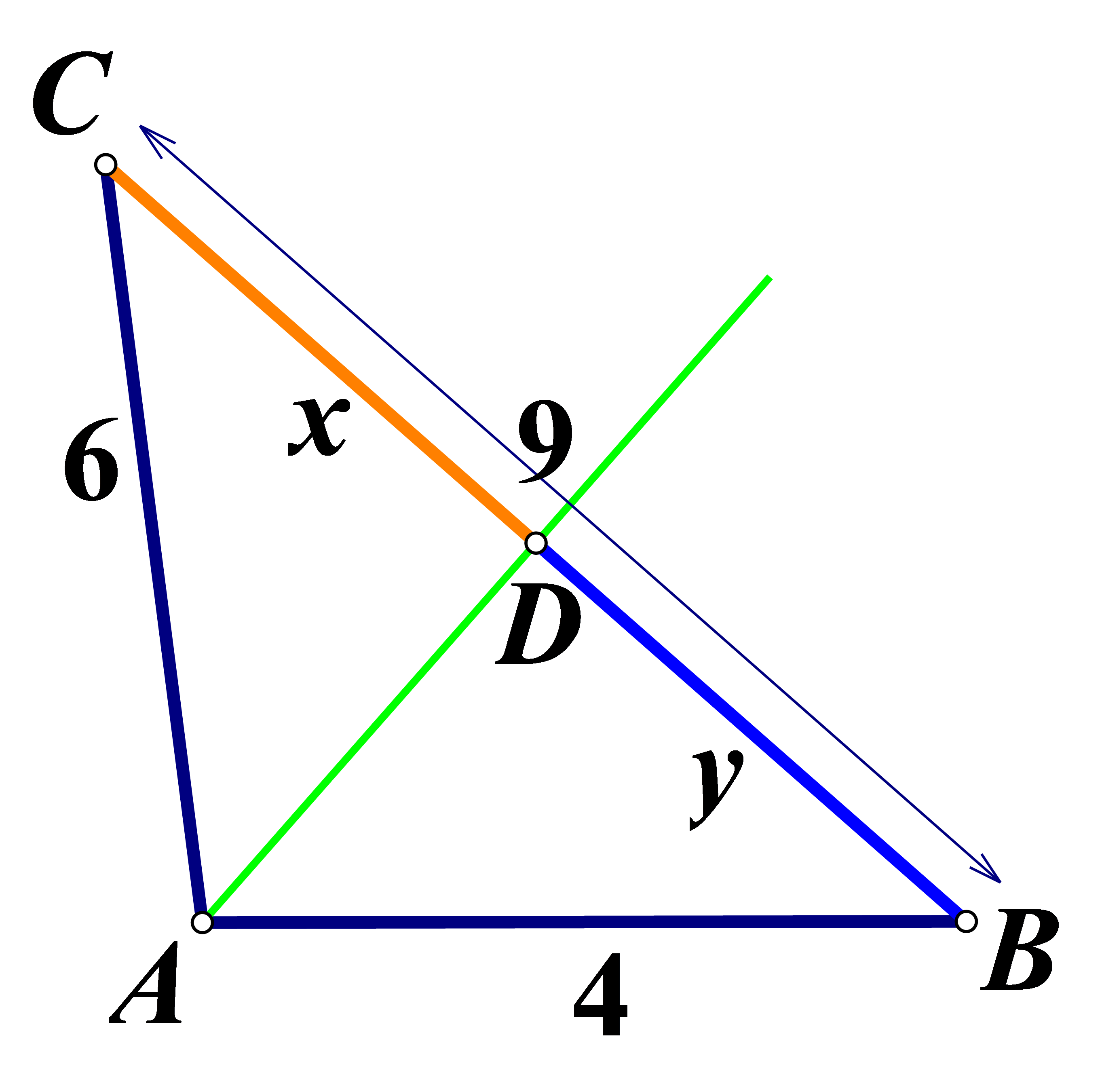
Izmjerite duljine dužina a zatim pokušajte odgovoriti.
Zanima nas i općenito, kako precizno odrediti omjer u kojem simetrala kuta u trokutu dijeli njemu nasuprotnu stranicu. Mijenjajte duljine stranica trokuta i promatrajte kako se mijenja taj omjer. Koristite sljedeću GeoGebrinu interakciju.
Simetrala kuta u trokutu dijeli njemu nasuprotnu stranicu u omjeru preostalih stranica. Ovu tvrdnju nazivamo Poučak o simetrali kuta u trokutu.
Dokažimo poučak o simetrali kuta u trokutu.
U svakom od sljedećih trokuta povučena je simetrala jednog od kutova. Duljine stranica trokuta označene su s
Koristeći se poučkom o simetrali kuta u trokutu, odredite nepoznate elemente.
Točka dijeli stranicu paralelograma u omjeru računajući od vrha Pravac siječe pravac u točki Odredite duljinu ako je
Produžeci krakova trapeza sijeku se u točki Izračunajte duljinu kraće osnovice i duljinu kraka ako je
U pravokutnom trokutu povučene su iz vrha pravog kuta težišnica i simetrala kuta. Težišnica siječe hipotenuzu u točki a simetrala u točki Ako je izračunajte duljine kateta trokuta
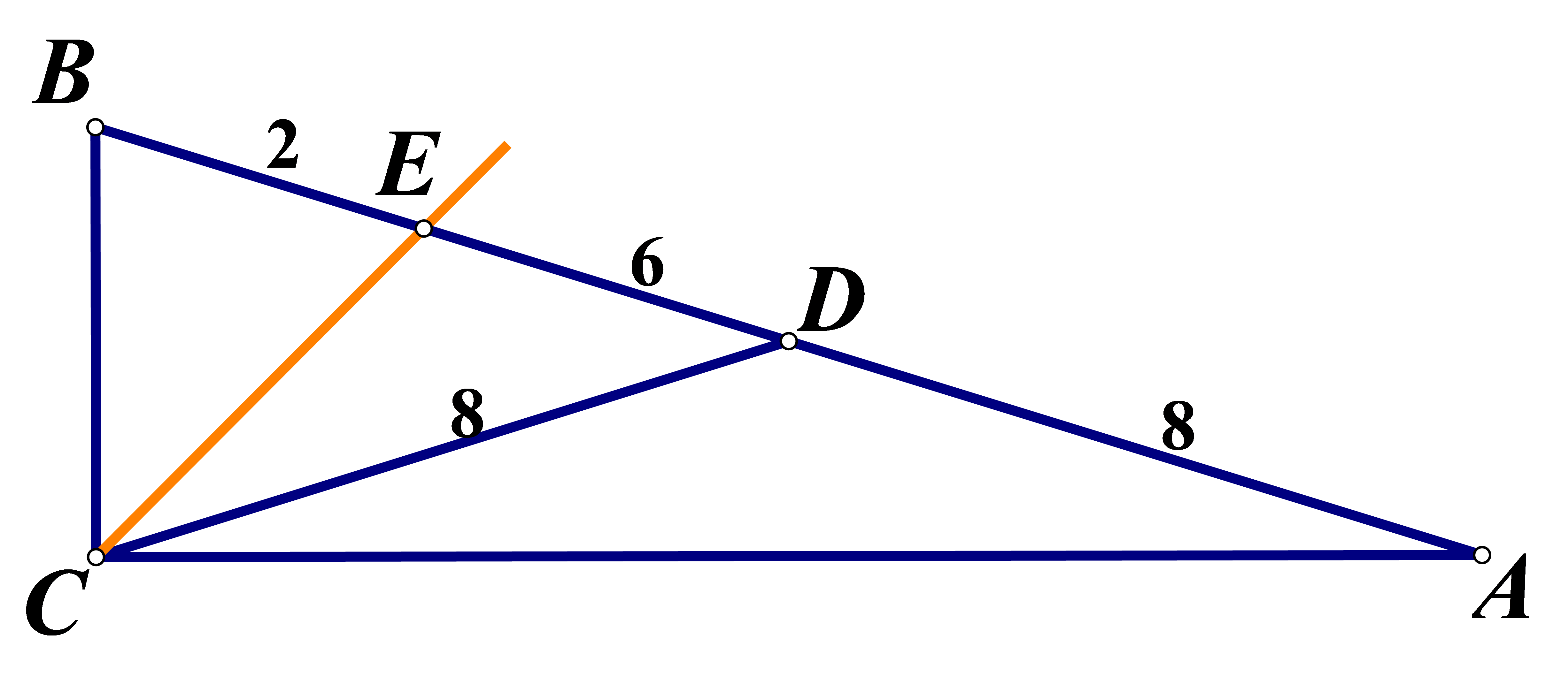
U pravokutnom je trokutu duljina težišnice jednaka polovici duljine hipotenuze.
Stoga je
Prema poučku o simetrali kuta u trokutu a prema Pitagorinu poučku jest
Slijedi
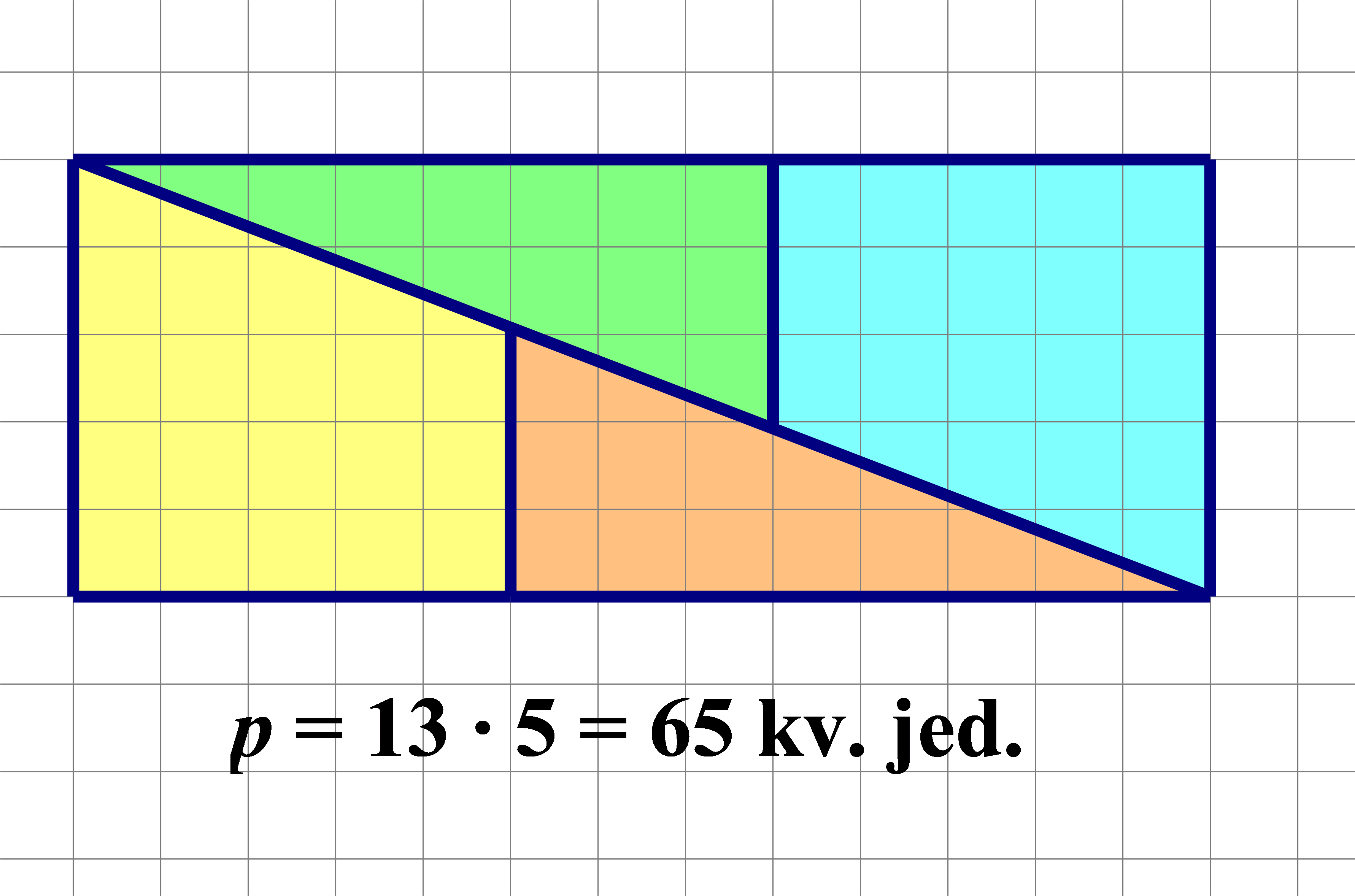
Kvadrat kojemu je stranica duljine
jediničnih dužina složen je od dva sukladna trapeza i dva sukladna pravokutna trokuta. Razrežemo li kvadrat i od istih likova složimo pravokutnik ili jednakokračan trokut kao na slikama, njihove bi površine trebale biti jednake površini početnog kvadrata.
Je li to doista tako? Obrazložite što je pogrešno?
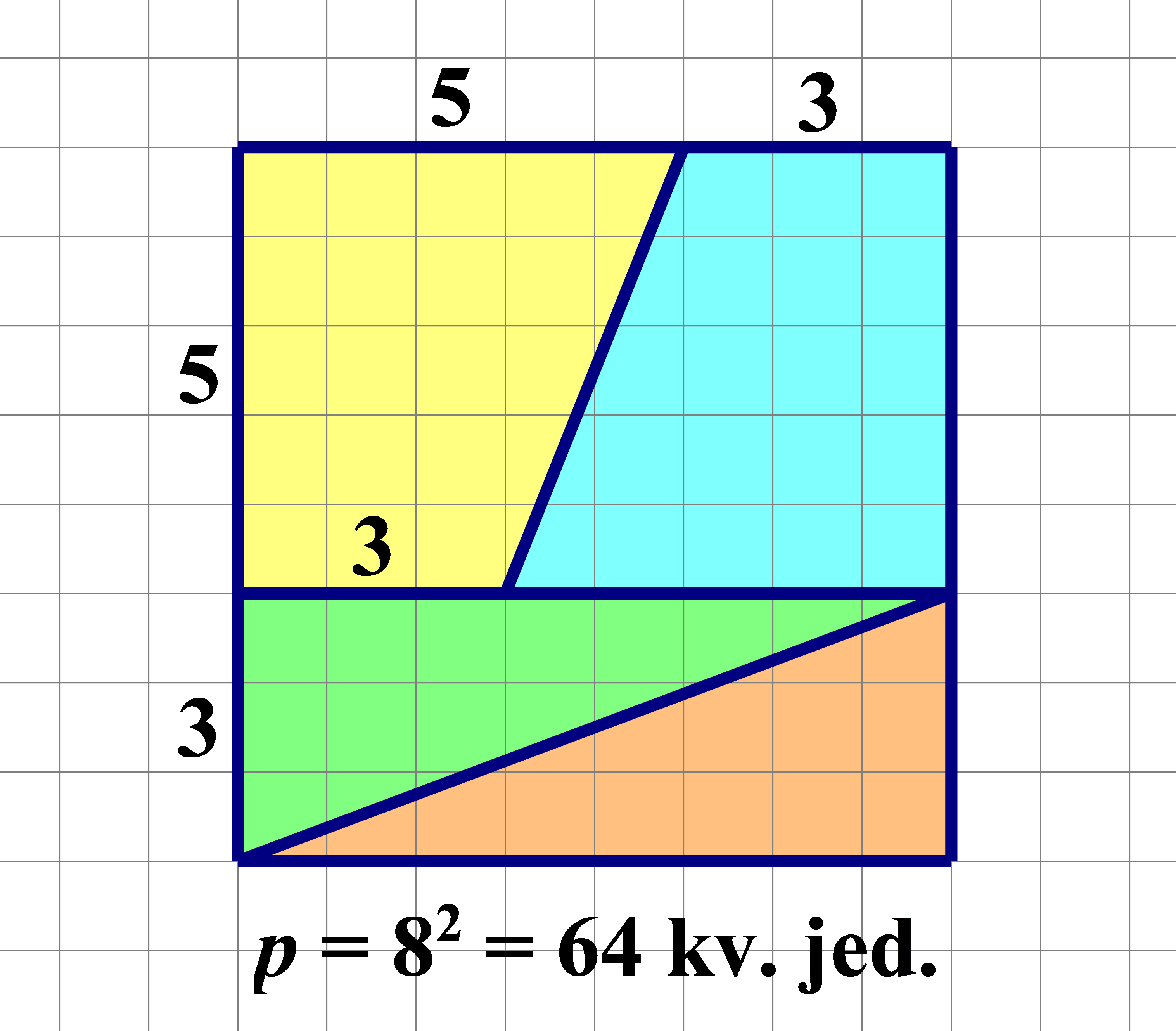
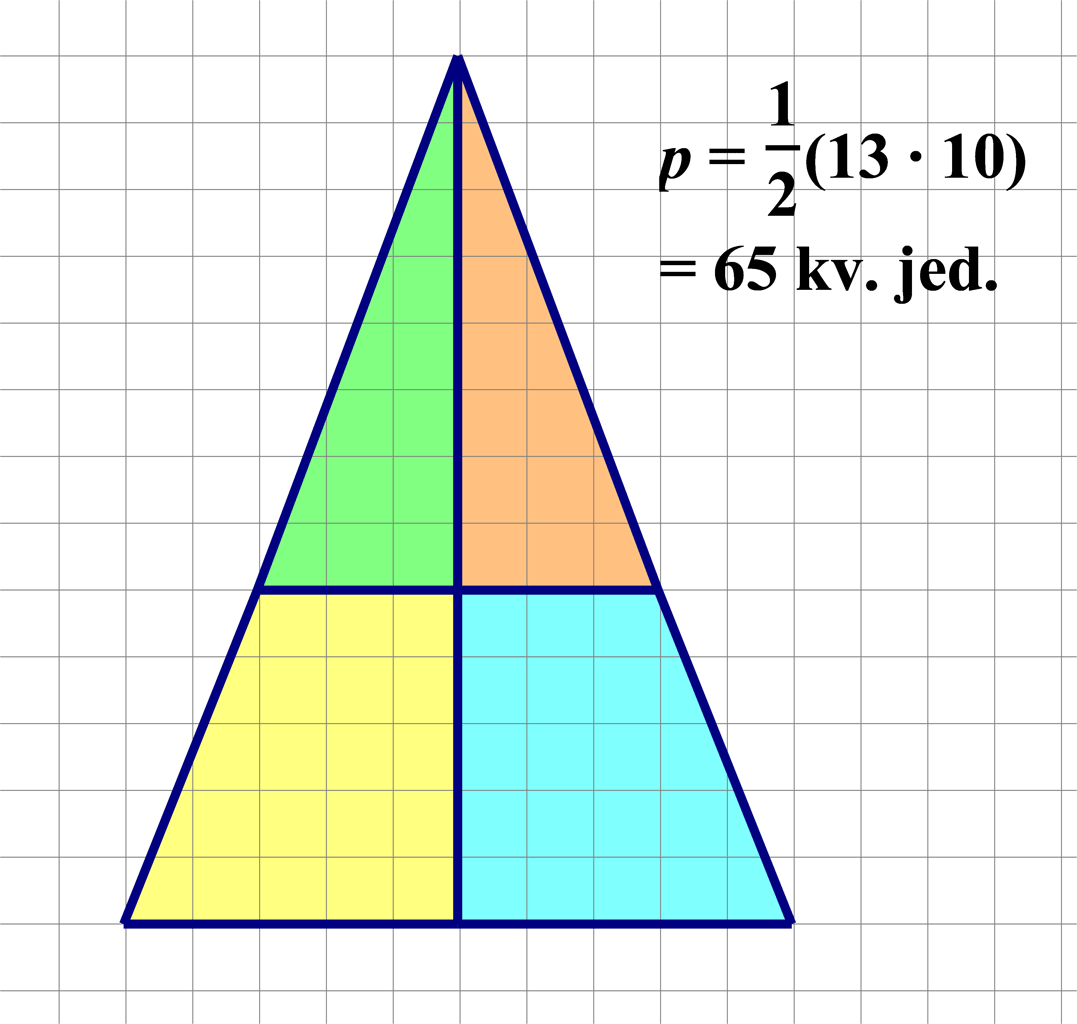
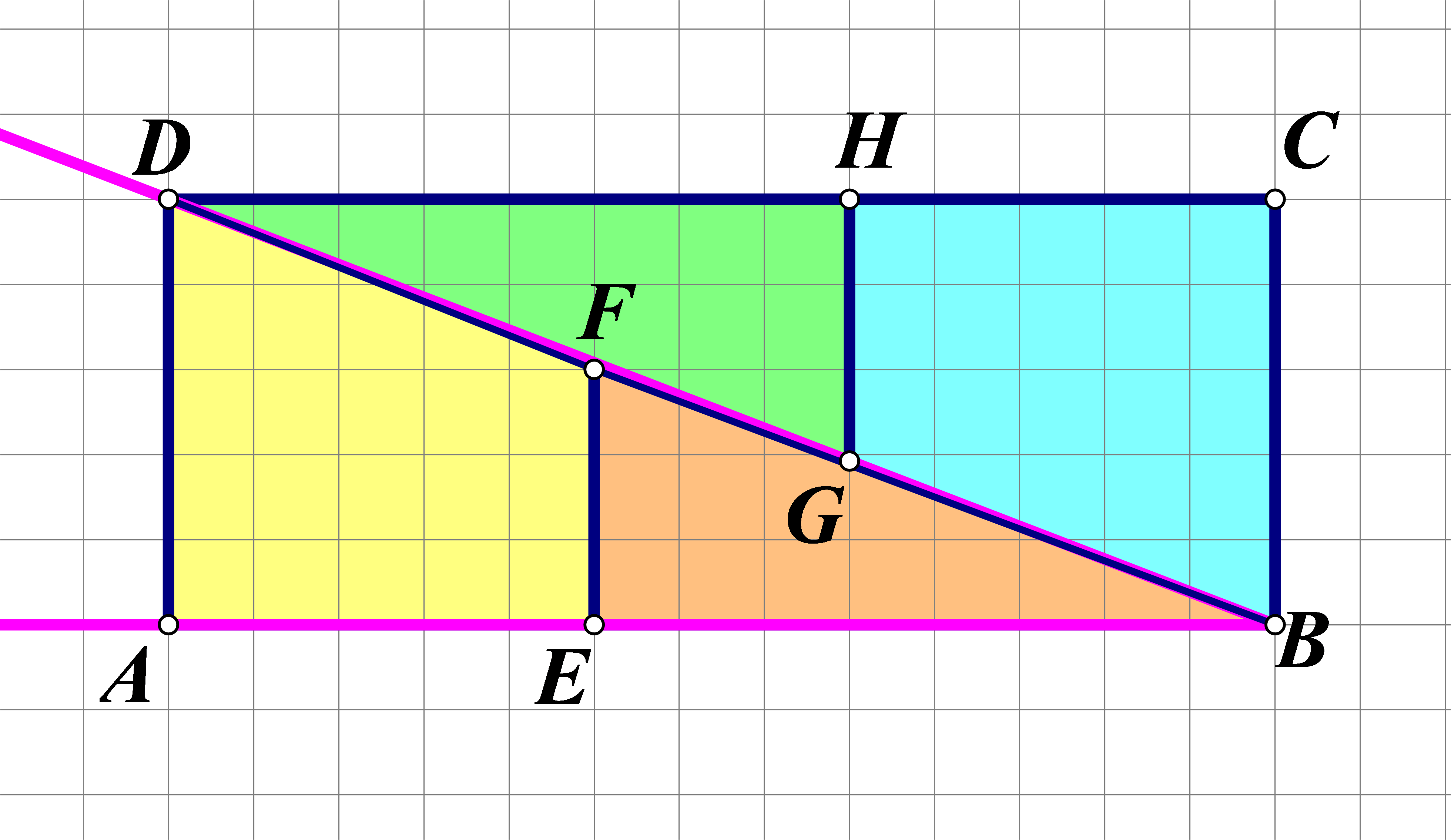
Postoji više načina da se obrazloži pogreška. Mi ćemo koristiti Talesov poučak o proporcionalnosti.
Promotrimo sliku. Pretpostavimo da su točke na jednom pravcu, odnosno kraku kuta On je presječen s dva paralelna pravca a tada prema Talesovu poučku o proporcionalnim dužinama vrijede sljedeći razmjeri:
što nije istinita jednakost.
Prema tome, kriva je početna pretpostavka da su točke
na istom pravcu. Analogno se pokaže i za točke
Stoga je višak površine nastao kod dijagonale, gdje se pojavljuje četverokut
koji ima površinu
kvadratnu jedinicu.